基于马尔科夫链模型的岱海地区气候变化周期研究
张振锋,游广永,赵元杰
(1.河北工业大学管理学院,天津 300130;2.中国科学院西双版纳热带植物园,云南勐腊 666303; 3.河北师范大学资源与环境科学学院,河北石家庄 050016)
基于马尔科夫链模型的岱海地区气候变化周期研究
张振锋1,游广永2,赵元杰3*
(1.河北工业大学管理学院,天津 300130;2.中国科学院西双版纳热带植物园,云南勐腊 666303; 3.河北师范大学资源与环境科学学院,河北石家庄 050016)
岱海湖相沉积物很好记录了近万年来区域气候变化的相关信息。利用马尔科夫链模型对岱海孢粉组合反映的气温和降水数据进行的周期性分析表明:该地区气候变化存在大约60 a、80 a、180 a、400 a、900 a等周期;周期变化与利用深水区沉积物、孢粉等研究结论以及相关地区的气候变化周期相一致,证明了马尔科夫链模型是研究环境变化周期性可利用的方法之一;在短时间尺度上,岱海地区气候变化与太阳活动和火山地震活动的周期存在相关性,太阳活动是该地区气候变化的主要驱动力之一,火山地震等因素对气候变化有一定的影响。
马尔科夫链模型;气候变化;周期;岱海
随着科技进步,古气候演化序列的重建已逐步实现。许清海等利用内蒙古岱海地区的孢粉记录建立了1万年来气候变化的序列,样本的时间间隔为24~140 a不等,初步的结果认为暖湿和冷干交替出现,每种气候状态具有200~800 a不同的持续时间[1]。基于随机性分析的马尔科夫链模型(Markov Chain Model)已广泛应用于自然灾害预测、植被演替、土地利用变化研究及降雨序列模拟预测等方面[2-4]。本文尝试将马尔科夫链模型应用于岱海地区气候变化序列研究中,探讨基于随机性理论的气候变化周期性。
1 马尔科夫链模型的基本原理
马尔科夫过程是随机过程理论中的一种,其主要原理是:若系统的随机过程 X(t)在时刻 t的状态用E表示,则在时刻τ(τ>t)系统所处状态与 t以前所处状态无关[5]。根据柯尔莫哥洛夫-开普曼定理,某一状态经过 n步转移后到其它状态的概率是一阶转移概率矩阵的n次自乘[6],当 n趋向于无穷大时,各状态的出现概率处于某一稳定值,即为下一时刻出现该状态的概率,而其倒数即为本文所计算的回归周期。
并非任何状态序列均可用马尔科夫链模型进行分析,马氏性检验是判断状态序列可否用马尔科夫链模型进行分析的关键。对于气温状态变化的时间序列,就是要检验各气温状态的发生是否独立事件。若非独立事件,其可构成一个状态之间有联系随机状态序列,并可用马尔科夫链模型进行分析。Anderson等提出的检验统计量为:

其中,-2lnλ的分布是渐进于自由度为(T-1)[m (m-1)]的χ2分布。m为状态数,T为时间(或空间)的子区间数。上式可变换为:
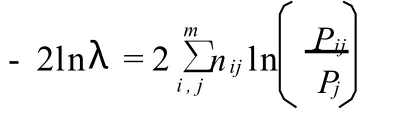
其中,Pij为一阶转移概率矩阵(TPM)中第(i,j)个元素,Pj为 j列的边缘概率,nij为转移频数矩阵中第(i,j)个元素,m为状态总数。
本文在数据序列的状态划分上采用统计学方法,将样本划分为4个状态空间。分组数确定后,通过调整状态空间的界限可以调整每一区间内的状态数量,然后进行马氏性检验。反复进行状态空间界限的调整和马氏性检验,最终确定可以用马尔科夫链模型进行分析的状态序列。
2 岱海盆地气候变化周期性分析方法
2.1 数据来源
岱海位于内蒙古高原南缘、乌兰察布盟凉城县(112°33′31″~112°46′40″E,40°29′7″~40°37′6″N),是一个封闭的内陆盆地。岱海湖相沉积物保存较完好,很好记录了区域气候变化的相关信息。现代气象资料显示,岱海盆地属于中温带半干旱季风气候,年均气温为5.1℃,最冷月平均气温为-13.0℃,最热月平均气温为20.5℃,年均降水量为423.7 mm。而利用孢粉-气候响应面分析得到的气温和降水数据显示,最热月平均气温为19.8℃,年均降水量为413.9 mm。
本文数据来源于基于孢粉-气候响应面及14C测年方法恢复的岱海地区近万年来的7月平均气温和年降水量资料[1](图1)。因此,即使是很小的气温变化也代表孢粉数量和孢粉组合的变化,并且代表古环境时期的气候状况。
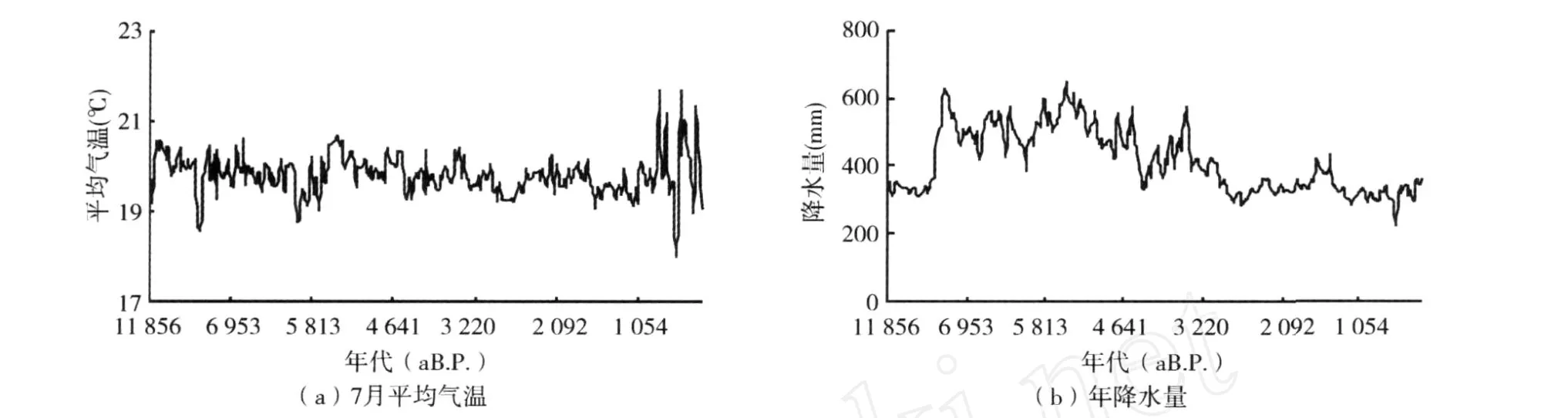
图1 岱海地区近万年来的7月平均气温和年降水量变化Fig.1 The average air temperature in July and annual precipitation in Daihai region for recent about 10 ka
2.2 数据分析方法
本文将此孢粉-气候响应面分析得到的所有数据的均值(7月平均气温19.8℃,年降水量413.9 mm)作为气候波动序列的平均值,并以此计算各样本的距平数(图2)。
由于所得数据的时间间隔为24~158 a[1],所以不能将所有数据作为随机序列进行处理,需要分段进行:1)将沉积速率不变的地层作为一个计算单元,即分别以24 a、33 a及40 a间隔作为一组,并以各组内部样本的平均值作为主要分界值;2)将所有数据等间隔处理后进行周期计算。分析时首先计算气候要素在该年代区间内的平均值,选取距平值作为状态划分的依据(图2)。部分年代(距今6 600~5 400 aB.P.)具有较明显的趋势,应先划分趋势线并以趋势线为界进一步划分状态。趋势线的添加采用一元线性回归(Y=a*X+b)的方法。

图2 岱海地区近万年来的7月平均气温和年降水量距平值Fig.2 Anomalies of average air temperature in July and annual precipitation in Daihai region for recent about 10 ka
3 气温与降水变化周期
3.1 最热月平均气温变化周期
岱海地区近万年来7月份平均气温距平值显示(图2),气温保持相对稳定,平均气温变幅较小。3.1.1 距今6 600~5 400 aB.P.(样本时间间隔为24 a) 该时段的气温波动计算结果显示(表1):B和C两个状态出现的周期是60 a左右;A和D两个状态的出现频率为150 a和200 a左右。由于该时段气温在高温水平中呈现出逐渐升高的趋势,为发现其中的波动性,分析时以一元线性趋势线(Y= 0.011*X-0.27)为基准上下移动0.15个单位,从而确定气温波动的3个状态区间,自下而上分别是A、B、C(表2)。可见,该时段的气温波动在添加趋势线前(表1)为60 a左右的周期;添加趋势线后(表2),A和C状态的回归周期与添加之前(-0.5,0)和(0,0.5)状态出现的周期大致相同。

表1 距今6 600~5 400 aB.P.气温回归周期计算结果Table 1 Regression periods of average air temperature in July for 6 600~5 400 aB.P.

表2 添加趋势线后距今6 600~5 400 aB.P.气温回归周期计算结果Table 2 Regression periods of average air temperature in July based on trendline for 6 600~5 400 aB.P.
3.1.2 距今2 800~1 300 aB.P.(样本时间间隔为24 a) 该时段的气温波动计算结果显示(表3):B和C两个状态出现的周期分别是60 a和90 a左右; A和D两个状态的出现频率为130 a左右。其中, 60 a的周期与上一时段有很好的对应,而134 a的周期接近上一时段150 a和120 a左右的气候波动周期。
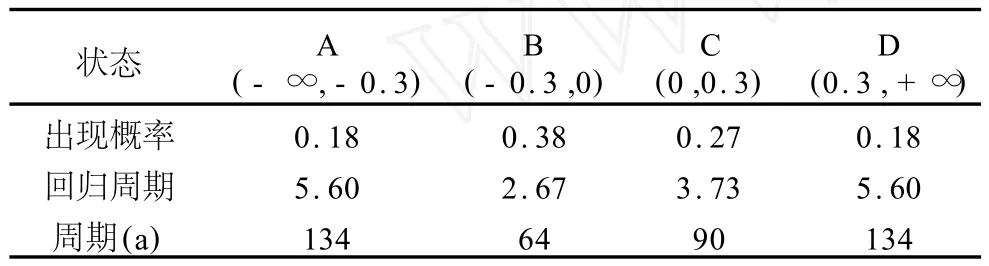
表3 距今2 800~1 300 aB.P.气温回归周期计算结果Table 3 Regression periods of average air temperature in July for 2 800~1 300 aB.P.
3.1.3 距今1 288~0 aB.P.(样本时间间隔为33 a) 该时段气温波动性不断增加,周期性计算结果显示(表4):气温在(-∞,-0.5)区间出现的周期为176 a,在(-0.5,0)区间出现的周期为136 a,在(0, 0.5)区间出现的周期为89 a,在(0.5,+∞)区间出现的周期为166 a。该时段与2 800~1 300 aB.P.的周期计算结果对比,发现该时段气温在 19.4~19.9℃和19.9~21.4℃区间的回归周期是89 a和135 a(表4),而在2 800~1 300 aB.P.期间,同样回归周期89 a和134 a出现的气温区间为19.6~19.9℃和19.9℃以上(表3)。所以可以认为:前后两个时段虽然气温的平均值略有变化,但其周期性保持不变,并且波动的程度增大。
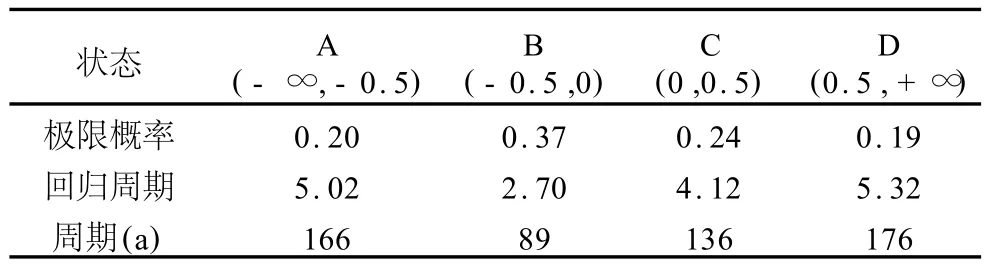
表4 距今1 288~0 aB.P.气温回归周期计算结果Table 4 Regression periods of average air temperature in July for 1 288~0 aB.P.
3.1.4 整列数据的等间隔化处理及周期计算 马尔科夫链的分析方法要求状态之间在等间隔的时间进行转化。气候在波动中有一定的稳定性,表现在周期的稳定上,所以固定时间间隔系统的状态向其它状态的转移有一定的规律。岱海地区数据序列的主要时间间隔为24 a、33 a、40 a。近似取其最小公倍数80 a,每隔3个24 a的样本取1个值,每隔两个33 a和40 a间隔的样本取1个值,近似建立以80 a为等间隔的数据序列,然后从中提取各状态间的转移频数和转移概率。
近万年来岱海地区的气温值较为稳定,平均值并没有很大变化,所以不用附加趋势线来划分气温状态。根据气温波动的幅度将其划分为4个状态(表5),并将转移频数转换为转移概率矩阵(表6)。对这一数据进行马氏性检验,发现界限为±0.5℃的状态划分方法置信水平在95%以上。

表5 气温波动幅度的转移频数矩阵Table 5 Transfer frequence matrix of fluctuation range of average air temperature in July
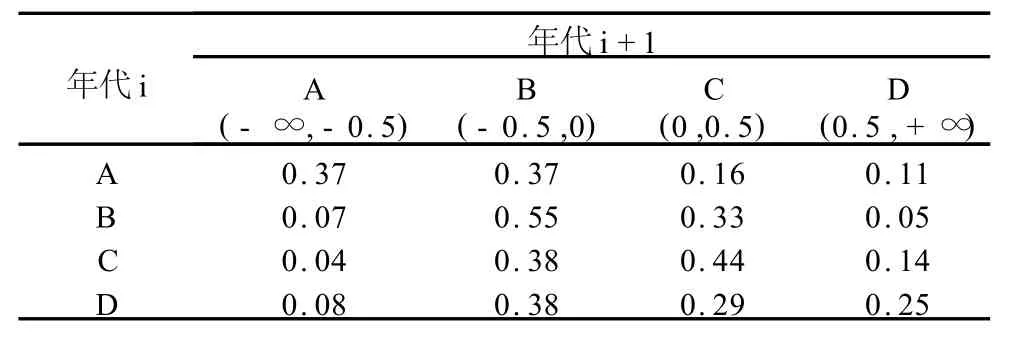
表6 气温波动幅度的转移概率矩阵Table 6 Transfer probability matrix of fluctuation rangeof average air temperature in July
对比各时段和总体数据之间周期计算的结果,发现总体数据(表7)中180 a的周期对应各时段中的90 a周期(表3、表4);240 a的周期对应各时段中的120 a和60 a左右周期(表1~表3)。

表7 各气温状态的出现概率和回归周期Table 7 Appearance probability and regression periods of every air temperature state
3.2 年降水量周期分析
近万年来岱海地区的降水值表现出逐渐降低的趋势,为显示其波动性,分析时以添加的趋势线为基准划分状态,以反映降水的波动情况。由于各时段的趋势线有不同斜率,所以在不同的时段采用不同的趋势线基准。
3.2.1 距今5 400~3 700 aB.P.(样本时间间隔为33 a) 该时段的降水波动性较大,在近1 700 a内波动近5次。周期性计算结果显示(表8):该时段降水量的波动周期为80 a、90 a和120 a左右,与气温的波动周期对应很好。

表8 距今5 400~3 700 aB.P.的降水周期Table 8 Precipitation periods for 5 400~3 700 aB.P.
3.2.2 距今2 800~1 300 aB.P.(样本时间间隔为24 a) 该时段的降水曲线显示了波动中逐渐减少的特点,计算结果也出现80 a左右的周期(表9),与同时期的气温波动周期(表3)略有不同;与上一时期的降水计算结果(表8)具有一致性,都出现了大致80 a和100 a的周期,同一气候状态的回归周期在两个时段中变化较小,表明气候在这一时期波动较为平稳。

表9 距今2 800~1 300 aB.P.的降水周期Table 9 Precipitation periods for 2 800~1 300 aB.P.
3.2.3 对整列降水数据的分析 为研究全新世以来降水量的波动性,以趋势线为基准将降水数据序列划分为4个状态,并按照气温分析中的取样方法对降水进行等间隔取值。降水的周期计算结果(表10)和各时段中的周期计算结果有一定的对应,400 a和200 a左右的周期对应100 a左右的周期。

表10 近万年来岱海地区降水周期Table 10 Precipitation periodicity in Daihai region for recent 10 ka
4 讨论
4.1 气候变化的周期性
马尔科夫链模型的周期计算结果表明,7月平均气温在近万年来各个阶段的波动都体现出了一致性,多次出现大约180 a、80 a和60 a的周期特征,降水的波动也多次出现大约90 a、80 a的周期,并且这种波动周期在各时段中都有体现。对近万年来所有数据的周期计算结果显示,气温的回归周期是降水回归周期的两倍。
4.2 周期性分析的可靠性
曹建廷等通过对岱海深水区沉积柱样的研究表明:岱海地区各气候状态的持续时间分别为200 a、110 a、150 a、90 a、60 a[7];许清海等的研究结果表明:200 a、100 a、80 a、60 a的气候状态持续时间出现次数较多,波动存在一致性[8];鲜锋等对青藏高原泥炭记录的总有机碳的频谱进行分析,发现在95%置信水平上存在1 428 a、512 a、255 a、217 a的准周期[9];徐国昌指出我国西部地区近1 000 a中的5次冷期(940~860 aB.P.,730~630 aB.P.,570~480 aB.P.,380~270 aB.P.和200~140 aB.P.),每次平均持续时间为180 a、90 a、60 a不等[10]。5 400~3 100 aB.P.期间,老虎山剖面的地层记录也显示出这一时期降水的频繁波动性[11],且与岱海地区的周期研究结果一致。以上分析结果和利用马尔科夫链模型计算的结果都表现出了很好的对应,表明完全可以应用马尔科夫链模型研究气侯变化的周期性。
4.3 气候变化周期的驱动力
岱海地区在全新世多次出现400 a、180 a和80 a左右的周期,表明气候的波动是不同因素共同作用的结果,不同时段表现出不同的主导周期。但是无论哪一种周期处于主导地位都与太阳活动的周期性相关[12,13],说明太阳活动是造成气温波动的主要原因。气温与强震的对应关系[14],基本对应了岱海地区气候变化周期计算中的60 a周期,说明地球内部系统的变化也可能是造成气候变化的原因之一。
4.4 影响计算结果的因素
数据计算中的不足主要表现在两方面:首先是分段计算周期数据量少,各状态间的转移概率矩阵误差大;其次,万年尺度内气候波动存在1 000 a或其它周期性波动,以不变的趋势线对气候状态进行划分,不仅使小周期的波动被隐藏,而且造成了周期计算的误差。另外,气温和降水的总体周期计算结果和其部分时段的周期计算结果存在一定的关系。结果的误差主要来源于年代测量、气温降水的量化、各状态区间的划分以及数据计算中的等间隔化等方面,这些误差导致气候波动周期的计算结果与其它地区周期计算结果有一定的偏差。
[1] 许清海,肖举乐,中村俊夫,等.孢粉资料定量重建全新世以来岱海盆地的古气候[J].海洋地质与第四纪地质,2003,23(4): 99-108.
[2] 钱家忠,朱学愚,吴剑锋.地下水资源评价中降水量的时间序列马尔科夫模型[J].地理科学,2001,21(4):350-353.
[3] 郭笃发.利用马尔科夫过程预测黄河三角洲新生湿地土地利用/覆被格局的变化[J].土壤,2006,38(1):42-47.
[4] 李凤娟,刘吉平.近百年长春市旱涝的马尔科夫链分析[J].吉林农业大学学报,2005,27(6):594-598.
[5] 王梓坤.随机过程论[M].北京:科学出版社,1978.
[6] 袁荫棠.概率论与数理统计[M].北京:中国人民大学出版社, 1989.
[7] 曹建廷,王苏民,沈吉,等.近千年来内蒙古岱海气候环境演变的湖泊沉积记录[J].地理科学,2000,20(5):391-396.
[8] 许清海,肖举乐,中村俊夫,等.孢粉记录的岱海盆地1500年以来气候变化[J].第四纪研究,2004,24(3):341-347.
[9] 鲜锋,周卫健,余华贵.全新世气候系统的突变及周期性[J].海洋地质与第四纪地质,2006,26(5):109-115.
[10] 徐国昌.中国干旱半干旱区气候变化[M].北京:中国气象出版社,1997.
[11] 张兰生,方修琦,任国玉.全球变化[M].北京:高等教育出版社,1999.
[12] STU IVER M,BRAZIUNAS T F.A tmospheric 14C and century-scale solar oscillations[J].Nature,1989,338:405-408.
[13] HONG Y T,JIANG H B,L IU T S,et al.Response of climate to solar forcing recorded in a 6000-yearδ18O time series of Chinese peat cellulose[J].The Holocene,2000,10(1):1-7.
[14] 郭增建.海洋中和海洋边缘的巨震是调节气候的恒温器之一[J].西北地震学报,2002,24(3):287.
Application of Markov Chain Model in Study on Periodicity of Climate Change in Daihai Region
ZHANG Zhen-feng1,YOU Guang-yong2,ZHAO Yuan-jie3
(1.School of M anagement,Hebei University of Technology,Tianjin300130;
2.Xishuangbanna Tropica l Botanical Garden,Chinese Academ y of Sciences,M eng la666303;
3.College of Resources and Environmental Sciences,Hebei N ormal University,Shijiazhuang050016,China)
Daihai isan enclosed inland basin,w hich is located in the southern edgeof Inner Mongolia Plateau.The lacustrine sediments in the basin has better reco rded the regional climate change information in recent about 10 ka.The periodicity analysison the data of air temperature and p recipitation obtained from the pollen assemblage analysis by means of Markov Chain Model show s that the climate change has some relatively stable periods such as60 a,80 a,180 a,400 a and 900 a,and so on.The periodicity is consistent w ith other research results by means of sediment in deeper water area and pollen analysis,also is consistent w ith the research results in other relative regions,w hich show s Markov Chain Model is one of available methods to study the periodicity of environmental change.In short time scale,there are relativities between Daihai regional climate change and solar activities,and volcanic earthquake activities,from w hich it is know n that the solar activities isoneofmain driving fo rces to cause climate change,earthquakes and volcano erup tions also impact on the periodicity of climate change to a certain extent.
Markov Chain Model;climate change;periodicity;Daihai
P467
A
1672-0504(2010)03-0082-05
2009-05-22;
2009-08-05
河北省自然科学基金项目(D2009000298);河北省软科学研究计划项目(09457293D);国家自然科学基金项目(40671188)
张振锋(1971-),男,博士研究生,从事生态环境研究。*通讯作者E-mail:ecoenvir@yahoo.cn

