五种常用降水量插值方法误差时空分布特征研究——以深圳市为例

邬 伦,吴小娟,肖晨超,田 原,3＊

(1.北京大学遥感与地理信息系统研究所,北京 100871;2.武汉大学遥感信息工程学院,湖北武汉430079; 3.香港理工大学土地测量及地理资讯学系,香港）

五种常用降水量插值方法误差时空分布特征研究
——以深圳市为例

邬 伦1,吴小娟2,肖晨超1,田 原1,3＊

(1.北京大学遥感与地理信息系统研究所,北京 100871;2.武汉大学遥感信息工程学院,湖北武汉430079; 3.香港理工大学土地测量及地理资讯学系,香港）

在洪水、滑坡等地质灾害预警预报中,通常需要对多个时点、多个站点的降水量观测数据进行高精度插值,雨量插值精度对灾害预警预报的可靠度具有很大的影响,因此研究降水量插值方法误差的时空分布特征具有重要的科研和实用价值。该文以深圳市2008年6月12日至14日百年一遇的强降水过程为例,采用交叉验证方法对反距离权重法、普通克里金法、全局多项式法、局部多项式法和径向基函数法五种常用空间插值方法误差的时空分布特征进行分析,研究成果可为根据雨量时空分布特点选取适用雨量插值模型提供相关依据,并为相关研究提供借鉴。

降水量;插值误差;误差时空分布特征;地质灾害;预警预报

0 引言

高质量的降水数据在水资源管理、水文建模、气候变化、地质灾害预警预报等方面具有重要应用[1]。实践中,雨量观测站点的布设受到地形、人力、财力等因素的限制,直接观测数据无法精确表达降水量的时空分布,通常需要采用空间插值方法对站点观测数据进行插值,以获取整个区域内降水量的总体分布数据。目前,空间插值方法在降水量插值方面得到了广泛应用。徐超在山东省境内分别采用反距离权重法、径向基函数法和普通克里金法对多年气象要素进行了空间插值分析,发现普通克里金法的插值效果更理想[2];朱芮芮等对日降雨量的时空变异特征进行分析,得出普通克里金法和反距离权重法总体效果较好[3];Bussires等在日累计降水量的插值研究中发现地统计学克里金法优于简单的泰森多边形法和反距离权重法[4];Dirks等比较了克里金法、反距离权重法、泰森多边形法在年、月、日、时四种时间分辨率情况下的插值结果,发现克里金法插值效果最好[5]。

前人研究表明,由于时间及空间尺度不同,适用的空间插值方法和降水模型也不相同[2-5]。目前降水量插值方法的空间和时间误差分布研究主要集中在空间插值方法对区域总体年、月、日累计降水量的插值效果方面,对于洪水、滑坡等地质灾害预警预报工作需要的更高时间和空间分辨率下插值方法的误差时空分布很少涉及。实践中,一次特大洪水的形成不但与前期累计雨量有关,也与致洪暴雨的时空分布特别是与暴雨量持续时间的长短有关[6];降水诱发的滑坡、崩塌等地质灾害发生的时间和区域与强降雨的时空分布也具有耦合性[7-9]。在这些应用中,不仅需要获得少数重点时点的累计雨量和分布情况,更需要获得高空间和时间分辨率的全过程雨量分布数据。因此,有必要对常见雨量插值方法在高空间和时间分辨率下的误差分布进行研究。

1 插值方法及其精度评价

1.1 插值方法

空间插值是利用已知的部分空间样本信息对未知的地理空间特征进行估计,也是 GIS的重要功能模块之一[10]。Dirks将空间插值方法归结为整体插值法和局部插值法[5],Vicente-Serrano等将插值方法细分为整体插值法、局部插值法、地学统计法和混合插值法[11]。雨量观测数据均为点数据,在对点数据进行插值时,常用的插值方法有五种:1）反距离权重插值法(Inverse Distance Weighting,IDW）,以插值点与样本点间的距离为权重进行加权平均,离插值点越近的样本点赋予的权重越大(本文采用反距离平方加权法[12]）;2）普通克里金插值法(Ordinary Kriging,OK）,是区域化变量的线性估计,但其考虑了空间相关性,更加符合空间数据的特点(本文用球形模型[13,14]）;3）全局多项式插值法(Global Polyno-m ial,GP）,以整个研究区的样点数据集为基础,用一个多项式计算预测值(本文采用二次多项式进行拟合）;4）局部多项式插值法(Local Polynomial,LP）,采用处在特定重叠邻近区域内的多个多项式进行插值,其产生的曲面更依赖于局部数据的变异(本文采用二次多项式进行拟合）;5）径向基函数插值法(Radial Basis Function,RBF）,是多个数据插值方法的组合,即经过各个已知样点生成一个圆滑曲面,并使表面的总曲率最小[15](本文采用张力样条函数作为基函数,并设置表面光滑度参数为2）。

1.2 插值精度评价

本文采用交叉验证法[16]评价各种方法的插值效果。研究中将50个站点随机排列并分为5组,每组10个站点,依次假设其中一组站点的降水量未知,用其余40个站点的降水量进行插值,得到所有站点所有时段的降水估计值,最后计算每个站点每时段实际观测值与估算值的误差。

误差评价指标采用平均绝对误差(MAE）、平均相对误差(M RE）和均方根误差(RM SE）。其中MAE反映估计值的误差范围,M RE反映估计值对于观测值的准确度,RM SE则反映估计值的灵敏度和极值情况[1,17]。表达式为:

其中:Za,i、Ze,i分别为第i个站点的实际观测值和插值预测值,n为验证站点数。

分别从时间和空间两个角度对上述插值方法的误差进行统计分析。首先计算全区各时点雨量观测值与插值结果之间的误差,以分析各插值方法误差在时间序列上的分布特征;之后计算各站点在整个降水过程中各时点观测值与估计值间的误差,以分析不同插值方法误差的空间分布特征。研究中绘制了MAE、M RE和RM SE在时间和空间序列上的变化曲线,并计算MAE、MRE和RM SE的均值、标准差、最大值和最小值,用以表达各种插值方法误差的时空分布特征,以及各插值方法误差与雨量极值出现的时间与空间位置间的关系。

2 实例研究

2.1 研究区概况及研究数据

深圳地处我国东南沿海,属亚热带季风气候,多台风、暴雨等灾害天气,年均降雨量1 879.8 mm、降雨日数145 d、暴雨11次左右,全年85%的雨量、90%的暴雨日数出现在4—9月。复杂的自然环境、气候条件和人类活动,使深圳洪涝、崩塌、滑坡等灾害频发[18]。

本研究以深圳市2008年6月12日至14日百年一遇强降水过程为例,选取降水较为集中的深圳市西部地区作为研究区,以研究区内工作状态良好、空间分布相对均匀的50个雨量站的观测数据作为雨量观测数据(图1）。降水持续36 h,以1 h为间隔共划分为36个时段。降水量最大值出现在第24个时段,高达1 602.2 mm;最小值出现在第34个时段,为13 mm。为了分析误差的空间分布特征,对50个站点按自西向东的顺序依次编号,其中13号站点累计降水量最大(526.9 mm）,31号站点累计降水量最小(105.3 mm）

图1 研究区位置与雨量计分布Fig.1 The distribution of rainfall gauges in the study area

2.2 插值过程及结果分析

笔者以A rcGIS软件为基础平台开发了交叉检验程序。使用的插值模块为A rcGIS的 Geostatistical Analyst,按照交叉检验方案对每个时点的观测数据进行了插值。

2.2.1 插值误差时间序列分布特征 利用交叉检验方法对各个时点的插值结果进行误差统计,计算出五种方法插值结果的M AE、M RE和RM SE(图2）。表 1列出了五种插值方法在时间序列上的MAE、M RE和RM SE与降水量的相关系数及各自的平均值、标准差、最大值和最小值。

对MAE的分析可以得出:OK方法的平均值、标准差和最大值均最小,说明其插值误差范围最小; RBF、IDW和LP方法次之;GP方法误差范围最大。对MRE的分析可以得出:LP方法的估值误差与观测值的比值最小,OK方法的比值最大。RMSE的平均值、标准差和最大值的比较结果具有一致性,即GP＞LP＞IDW＞RBF＞OK。表1中相关系数表明:所有方法的MA E与RM SE和降水量呈正相关,表明降雨量大的时刻误差范围和误差极值都较大;而MRE与降水量呈负相关,表明降雨量大的时刻雨量估计值相对于观测值的准确度较高。

图2 五种插值方法插值误差的时间序列分布Fig.2 Temporal distributions of errors of five interpolation models

表1 五种插值方法时间序列误差指标分析Table 1Analysis on temporal distributions of errors of five interpolation models

进一步比较各种插值方法在降水量极值时点的插值效果,表2列出各种方法的 M AE、M RE和RMSE。在降水量最大时段,OK方法误差最小,GP方法误差最大;在降水量最小时段,GP方法误差最小,而RBF方法误差最大。

综合上述分析,从时间序列看五种插值方法中OK方法的误差总体最小,这与文献[3-5]的研究结果一致,且其在降水量最大的时段误差远小于其他4种方法;RBF方法和IDW方法的误差居中;LP方法和GP方法的误差整体偏大,但较适合于降水量小的时段。

2.2.2 插值方法误差空间分布特征 依次对每个站点各时点插值结果进行误差统计,计算出每个站点在整个降水过程中的MAE、MRE和RM SE(图3）。表3列出了各种插值方法插值结果在各个站点MAE、M RE和RM SE与降水量的相关系数及各自的平均值、标准差、最大值和最小值。各插值方法在各站点MA E、M RE和RM SE的误差分布表现与其在时间序列上的误差表现基本一致:OK方法的误差最小;RBF、IDW和LP方法误差居中;GP方法插值误差最大,且极值情况最为严重。表3中相关系数总体规律与表1类似:所有插值方法在空间分布上的MAE和RM SE均与对应站点的降水量呈正相关,表明在降水量较大的站点误差范围和误差极值都较大;而MRE与对应站点的降水量呈负相关,表明在降水量较大的站点雨量估计值相对于观测值的准确度较高。

为了进一步分析各插值方法在雨量极值站点的插值表现,表4列出了各种插值方法在降水量最大的站点和降水量最小的站点上的MAE、MRE和 RM SE。在降水量最大的站点,OK方法总体误差最小,GP方法误差最大;在降水量最小的站点,IDW方法误差最小,GP方法误差最大。

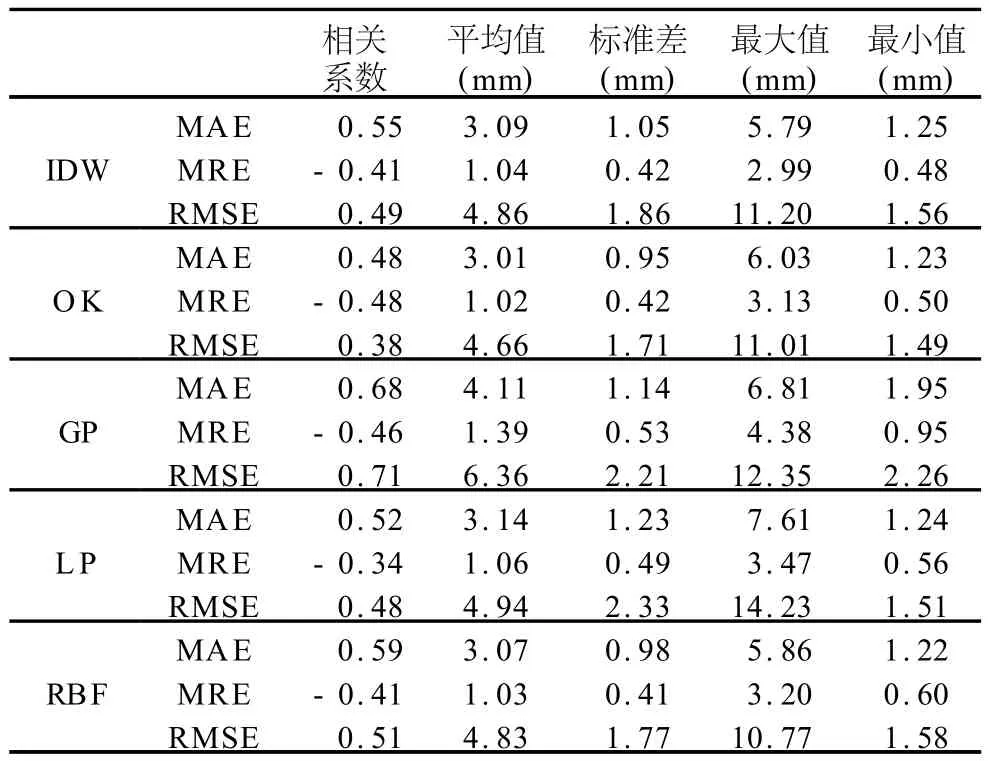
表3 五 种插值方法空间分布误差指标分析Table 3Analysis on spatial distributions of errors of five interpolation models

表4 五种插值方法在降水量最大、最小站点误差值Table 4 Errors of five interpolation modelsat themaximum and m inimum precipitation locations

3 结论与展望

对五种常见雨量插值方法误差的时空分布特征进行对比分析,可得出以下结论:1）在时间序列和空间点位分布上,OK方法总体误差最小,RBF和IDW方法总体误差次之,LP和 GP方法总体误差最大。2）在时间序列和空间点位分布上,各种插值方法的MAE和RM SE均与对应时刻或站点的降水量呈正相关,M RE则与之呈负相关。3）在时间序列上,在降水量最大的时段,OK方法误差最小,GP方法误差最大;在降水量最小的时段,GP方法误差最小,而RBF方法误差最大。4）在空间分布上,在降水量最大的站点,OK方法误差最小,GP方法误差最大,这与各插值方法的雨量最大值时刻的误差对比结果一致;在降水量最小的站点,IDW方法误差最小,GP方法误差最大。

五种常见雨量插值模型的插值误差有着不同的时空分布特征,总体而言,O K方法适用于降水量较大的时段和区域,IDW方法则适用于降水量较小的时段和区域,在选用时可以综合考虑。为取得更好的插值精度,还可以进一步考虑在一个降水过程中针对不同的降雨时段或区域采用不同的插值方法。

[1] 宋丽琼.日降水量的空间插值方法与应用对比分析——以深圳市为例[J].地球信息科学,2008,10(5）:566-572.

[2] 徐超,吴大千,张治国.山东省多年气象要素空间插值方法比较研究[J].山东大学学报(理学报）,2008,43(3）:1-5.

[3] 朱芮芮,李兰,王浩,等.降水量的空间变异性和空间插值方法的比较研究[J].中国农村水利水电,2004(7）:25-28.

[4] BUSSIRESN,HOGGW.The objective analysisof daily rainfall by distance weighting schemes on a mesoscale grid[J].A tmosphere-Ocean,1989,27(3）:521-541.

[5] DIRKS K N,HAY J E,STOW CD,et al.High-resolution studies of rainfall on Norfolk Island.Part II:Interpolation of rainfall data[J].Hydrology,1998,208:187-193.

[6] 赵玉春,王仁乔.一次致洪暴雨的中尺度分析[J].气象科技, 2005,33(3）:245-249.

[7] BRAND E W,PREMCH ITT J,PH ILL IPSON H B.Relationship between rainfall and landslides in Hong Kong[A].Proceedings of the Fourth International Symposium on Landslides, To ronto,1984,1:377-384.

[8] JIA G Y,TIAN Y,L IU Y,et al.A static and dynamic factorscoupled forecasting model of regional rainfall-induced landslides:A case study of Shenzhen[J].Science in China Series ETechnological Sciences,2008,51:164-175.

[9] TIAN Y,XIAO C C,L IU Y,et al.Effects of raster resolution on landslide susceptibility mapping:A case study of Shenzhen [J].Science in China Series E-Technological Sciences,2008,51: 188-198.

[10] LAM N.Spatial interpolation methods:A review[J].The American Cartographer,1983,10(2）:129-150.

[11] V ICENTE-SERRANO S M,SAZ-SÁNCHEZ M A,CUADRAT J M.Comparative analysisof interpolationmethods in themiddle Ebro Valley(Spain）:Application to annual p recipitation and temperature[J].Climate Research,2003,24(2）:161-180.

[12] PATRICK M B,KELLER C P.Multivariate interpolation to incorporate thematic surface date using inverse distance weighting (IDW）[J].Computer&Geosciences,1996,22(7）:795-799.

[13] PARDO-IGUZQU IZA E,DOWD P A.The second-order stationary universal Kriging model revisited[J].Mathematical Geology,1998,30(4）:347-378.

[14] KARN IEL IA.Application of Kriging technique to areal p recipitation mapping in A rizona[J].GeoJournal,1990,22(4）: 391-398.

[15] 王树良,史文中,李德毅,等.基于张力样条插值函数的土地数据挖掘[J].计算机工程与应用,2003,39(25）:5-7.

[16] SEAMAN R S.Objective analysis accuracies of statistical in-terpolation and successive correction schemes[J].Australian Meteorological Magazine,1983,31:225-240.

[17] 高华喜,殷坤龙.降雨与滑坡灾害相关性分析及预警预报阈值之探讨[J].岩土力学,2007,28(5）:1055-1060.

[18] 李朝奎,陈良,王勇.降水量分布的空间插值方法研究——以美国爱达荷州为例[J].矿产与地质,2007,21(6）:684-687.

On Temporal and Spatial Error Distributions of Five Precipitation Interpolation M odels:A Case of Shenzhen

WU Lun1,WU Xiao-juan2,XIAO Chen-chao1,TIAN Yuan1,3
(1.Institute of RS and GIS,Peking University,Beijing 100871;
2.Institute of Remote Sensing and Inform ation Engineering,W uhan University,W uhan 430079;
3.Department of Land Surveying and Geo-Informatics,Hong Kong Polytechnic University,Kow loon,Hong Kong,China）

Precipitation isan impo rtantmeteorological elementw idely used in the fo recasting of many kindsof natural disasters, such as floods and landslides.Typically,interpolation models are app lied to calculate the p recipitation distribution over the wo rking area based on limited observation data.It is important to study the tempo ral and spatial error distribution of p recipitation interpolation models to get p recise p recipitation data and to make the disaster fo recasting more credible.Five typical interpolationmodels,Inverse Distance Weighted,Ordinary Kriging,Global Polynomial,Local Polynomial,and Radial Basis Function,are chosen to carry a case study of Shenzhen,based on observation data of a rainfall p rocess between June 12 and June 14,2008.It can be concluded that the erro rsof all the fivemethods are highly relevant to p recipitation.Considering both the time and space series distribution,the erro rsof Ordinary Krigingmethod areminimum of all and the erro rsof Local Polynomial and Global Polynomial are themaximum.A t the moment of maximum p recipitation and at the locations of maximum p recipitation,Ordinary Kriging method has theminimum errors w hile Global Polynomialmethod has themaximum errors.But at themoment of minimum p recipitation,the errors of Global Polynomial,Local Polynomial and Inverse Distance Weighted are smaller than that of Ordinary Kriging,w hile erro rsof Radial Basis Function is themaximum.On the location of minimum p recipitation,the errorsof Inverse Distance Weighted and Global Polynomial are maximum and minimum respectively.The conclusions of this study may p rovide useful guidance on choosing suitable interpolation model.

p recipitation;interpolation erro r;tempo ral and spatial error distribution;geological disaster;forecasting and warning

P208;P426.6

A

1672-0504(2010）03-0019-06

2010-01-22;

2010-03-31

国家科技支撑计划课题(2008BAJ11B04、2006BAJ14B04）;国家自然科学基金项目(40701134、40928001）;国家高科技研究发展计划项目(2007AA 120502）;香港理工大学研究基金(Project No.G-U632）

邬伦(1964-）,男,教授,博士生导师,研究方向为地理信息科学。＊通讯作者E-mail:tianyuanpku@pku.edu.cn