Global and Blow-up Solutions to a p-Laplace Equation with Nonlocal Source and Nonlocal Boundary Condition∗

GUO BIN,WEI YING-JIE AND GAO WEN-JIE

(Institute of Mathematics,Jilin University,Changchun,130012)

Global and Blow-up Solutions to a p-Laplace Equation with Nonlocal Source and Nonlocal Boundary Condition∗

GUO BIN,WEI YING-JIE AND GAO WEN-JIE

(Institute of Mathematics,Jilin University,Changchun,130012)

This paper deals with an evolutionp-Laplace equation with nonlocal source subject to weighted nonlocalDirichletboundary conditions.We give sufficient conditions for the existence of global and non-global solutions.

nonlocal boundary condition,evolutionp-Laplace,nonlocal source, blow-up

1 Introduction

In this paper,we consider the following problem:

In the past several decades,many physical phenomena have been formulated as nonlocal mathematical models(see[1]and[2]).It has also been suggested that nonlocal growth terms present in a more realistic model in physics for compressible reactive gases.Problem (1.1)arises in the study of the flow of a fl uid through a porous medium with an integralsource(see[3]and[4])and in the study of population dynamics(see[5]and[6]).There have been many articles which deal with properties of solutions to local semilinear parabolic equations with homogeneous Dirichlet boundary condition(see[1],[7]and the references therein).However,there are some important phenomena formulated as parabolic equations which are coupled with nonlocal boundary conditions in mathematical modelling such as thermoelasticity theory(see[8]and[9]).In this case,the solution u(x,t)describes entropy per volume of the material.The problem of nonlocal boundary conditions for linear parabolic equations of the type

was studied by Friedman[10].It was proved that the unique solution of(1.2)tends to 0 monotonically and exponentially as t→+∞provided

As for more general discussions on the dynamics of parabolic problem with nonlocal boundary conditions,one can see,e.g.,[11],where the problem

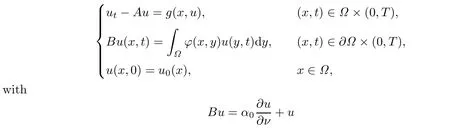
was considered and recently Pao[12]gave the numerical solutions for di ff usion equations with nonlocal boundary conditions.

The scalar problems with both nonlocal sources and nonlocal boundary conditions have been studied as well.For example,a problem of the form

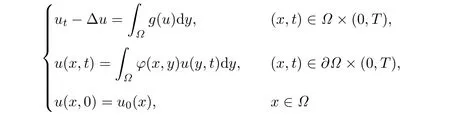
was studied by Lin and Liu[13].They established local existence,global existence and nonexistence of solutions,and discussed the blow-up properties of solutions.

In[14],Wanget al.studied the following problem:

in the case of g(u)=upwith m＞1,p＞1.They obtained the blow-up condition and its blow-up rate estimate.

In[15],Yanget al.considered the following problem:

They established global existence conditions for solutions to a nonlocal porous medium equation subject to nonlocal boundary conditions,and discussed the blow-up properties of solutions.

Non-Newtonian fi ltration equations and the equations of non-Newtonian fi ltration type with source or local boundary conditions have been extensively studied(see[17]and[18] and the references therein).Motivated by above works,we are interested in the blow-up properties of problem(1.1).The aim of this paper is twofold.Firstly,we use a similar method of[18]to give a comparison principal.Secondly,we establish the global existence and finite time blow-up of the solution.Our main results can be stated as follows.

Theorem 1.1Suppose thatZ

Ifm+n＞1,then the solution of(1.1)blows up in finite time for any positive initial data.

Theorem 1.2Suppose thatZ

(1)Ifp＞max{m+n+1,2},then every nonnegative solution of(1.1)exists globally;

(2)Ifp=m+n+1＞2,and|Ω|is sufficiently small,then the solution of(1.1)exists globally for sufficiently small initial data;

(3)If2＜ p＜ m+n+1,m+n＞1,then the solution of(1.1)exists globally for sufficiently small initial data,while it blows up in finite time for large initial data.

LetΦ(r)be the solution of the elliptic problem

To describe conditions for blow-up of solutions,we need the following assumptions on the initial data u0(x):

In the special case of n=p−1,m=0 or m=p,n=0,we have the following optimal results:

Theorem 1.3Suppose thatu0(x)satis fies the condition(H)and the following conditions hold:

(1)n=p−1,m=0orm=p,n=0;

(2)Ω contains a sufficient large ballBR(0);

Then the solution of(1.1)blows up in finite time.

This paper is organized as follows.Section 2 deals with the comparison principle used for the model.Theorems 1.1 and 1.2 are proved in Section 3.The special cases n=p−1, m=0 and m=p,n=0 are discussed in the last section.

2 Comparison Principle

In this section,we start with the de fi nition of super-solution and sub-solution of(1.1)and comparison principle.LetΩT=Ω×(0,T)and ST=∂Ω×(0,T).

De fi nition 2.2We say that the solutionu(x,t)of(1.1)blows up in finite time if there exists a positive constantT∗＜∞,such that

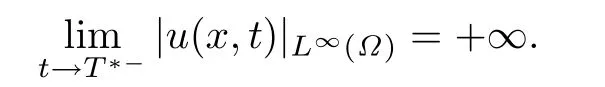
We say that the solutionu(x,t)exists globally if

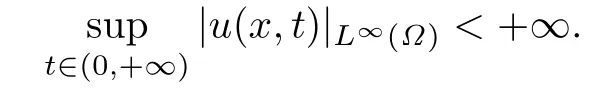
The following comparison principle plays a crucial role in our proof which can be obtained by similar arguments as those in[18].

Theorem 2.1Letu(x,t)andv(x,t)be a nonnegative sub-solution and super-solution, respectively,withu0(x)≤v0(x)forx∈u≤vin ΩT.

3 Proofs of Theorems 1.1 and 1.2

Compared with usual homogeneous Dirichlet boundary data,the weight function φ(x,y) plays an important role in the global existence or global nonexistence results for(1.1).

Proof of Theorem 1.1We consider the ODE

It is well known that the solution to(3.1)blows up in finite time if m+n＞1.By the comparison theorem,we get the global nonexistence result of(1.1).

Lemma 3.1[19,20]Let Ψ(x)be the unique positive solution of the following elliptical problem:

Then w(x,t)de fi ned as(3.2)is a super-solution of(1.1).By Theorem 2.1,we know that u(x,t)≤w(x,t),and then u(x,t)exists globally.

(2)The case of n=p−m−1.Choose

By(3.4)and(3.5),we know that w(x,t)is a super-solution of(1.1),and then we obtain that u(x,t)exists globally.

(3)The case of n＞p−m−1 and m+n＞1.We have two different results.Firstly,we prove the globally result.Choose

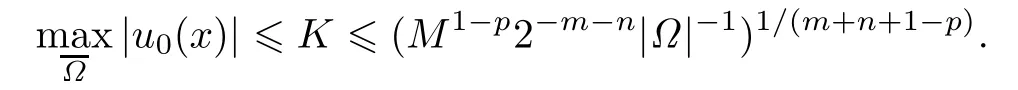
The proof is similar to the above one.By(3.3)and(3.4),we obtain that u(x,t)exists globally.On the other hand,to prove the blow-up result,we let φ∈C1(Ω),φ>0,φ0 and φ|∂Ω=0.By translation,we may assume,without loss of generality,that 0∈Ω,φ(0)＞0.

Since φ(0)＞0 and φ is continuous,there exist two positive constants ρ and ǫ such that

Then w≤0 on∂Ω×(0,T).From(3.6)it follows that w(x,0)≤K0φ(x)for sufficiently large K0.By Theorem 2.1,we get

and u can exist no later than t=T.This shows that u(x,t)blows up in finite time for large initial data.

4 Proof of Theorems 1.3

Proof of Theorems 1.3In the case of m=p,n=0,to prove the blow-up result,we consider the following problem(see[17]):

Let v(x,t)be the solution of this problem.It is obvious that v(x,t)is a sub-solution of problem(1.1).It is known to all that v(x,t)blows up in finite time if u0(x)is large enough. By Theorem 2.1,the solution of(1.1)blows up in finite time.

Lastly,consider the case of n=p−1,m=0.Without loss of generality,we can assume that 0∈Ω.Denote by BR(0)a ball centering at 0,with radius R and satisfying BR(0)⊂⊂Ω.By the assumptions on u0(x),we choose sufficiently small constant S0so that

By Theorem 2.1,we get W(x,t)≤u(x,t)onΩT.Thus u must blow up in finite time.

[1]Souplet,P.,Uniform blow-up pro fi les and boundary behavior for di ff usion equations with nonlocal nonlinear source,J.differential Equations,153(1999),374–406.

[2]Esteban,K.,Bimpong Bota,Ortoleva,P.and Ross,J.,Far-from-equilibrium at local sites of reaction,J.Chem.Phys.,60(1974),3124–3133.

[3]Galaktionov,V.A.,On asymptotic self-similar behavior for a quasilinear heat equation:Single point blow-up,SIAM J.Math.Anal.,26(1995),675–693.

[4]Samarskii,A.A.and Kurdyumov,S.P.,Blow-up in Problems for Quasilinear Parabolic Equations,Nauka,Moscow,1987(in Russian),Walter de Gruyter,Berlin,1995.

[5]Cantrell,R.S.,Di ff usive logistic equations with inde finite weights:Population models in disrupted environments II,SIAM J.Math.Anal.,22(1989),1043–1064.

[6]Furter,J.and Grin field,M.,Local vs.nonlocal interactions in populations dynamics,J.Math. Biol.,27(1989),65–80.

[7]Giga,Y.and Kohn,R.V.,Asymptotically self-similar blow-up of semilinear heat equations,Comm.Pure Appl.Math.,38(1985),297–319.

[8]Day,W.A.,Extensions of property of heat equation to linear thermoelasticity and other theories,Quart.Appl.Math.,40(1982),319–330.

[9]Day,W.A.,A decreasing property of solutions of parabolic equations with applications to thermoelasticity,Quart.Appl.Math.,40(1983),468–475.

[10]Friedman,A.,Monotonic decay of solutions of parabolic equations with nonlocal boundary conditions,Quart.Appl.Math.,44(3)(1986),401–407.

[11]Pao,C.V.,Asymptotic behavior of solutions of reaction di ff usion equations with nonlocal boundary conditions,J.Comput.Appl.Math.,88(1998),225–238.

[12]Pao,C.V.,Numerical solutions of reaction di ff usion equations with nonlocal boundary conditions,J.Comput.Appl.Math.,136(2001),227–243.

[13]Lin,Z.G.and Liu,Y.R.,Uniform blow-up pro fi les for di ff usion equations with nonlocal source and nonlocal boundary,Acta Math.Sci.Ser.B,24(2004),443–450.

[14]Wang,Y.,Mu,C.and Xiang,Z.,Blow up of solutions to a porous medium equation with nonlocal boundary condition,Appl.Math.Comput.,192(2007),579–585.

[15]Cui,Z.J.and Yang,Z.D.,Roles of weight functions to a nonlinear porous medium equation with nonlocal source and nonlocal boundary condition,J.Math.Anal.Appl.,342(2008),559–570.

[16]DiBenedetto,E.,Degenerate Parabolic Equations,Springer-Verlag,Berlin,New York,1993.

[17]Zhao,J.,Existence and nonexistence of solutions for ut−(div|∇u|p−1∇u)=f(∇u,u,x,t),J. Math.Anal.Appl.,172(1993),130–146.

[18]Li,F.C.and Xie,C.H.,Global and blow-up solutions to a p-Laplacian equation with nonlocal source,Comput.Math.Appl.,46(2003),1525–1533.

[19]Diaz,J.I.,Nonlinear Partial differential Equations and Free Boundaries,in:Elliptic Equations,vol.1,Pitman,London,1985.

35D05,35K15

A

1674-5647(2010)03-0280-09

date:Jan.21,2010.

The NSF(10771085)of China and the 985 Program of Jilin University.