A Uniaxial Optimal Perfectly Matched Layer Method for Time-harmonicScattering Problems∗

YANG XIAO-YING,MA FU-MING, ZHANG DE-YUEAND DU XIN-WEI

(1.College of Foundamental Science,Changchun University of Technology,Changchun,130012)

(2.School of Mathematics,Jilin University,Changchun,130012)

A Uniaxial Optimal Perfectly Matched Layer Method for Time-harmonic
Scattering Problems∗

YANG XIAO-YING1,2,MA FU-MING2, ZHANG DE-YUE2AND DU XIN-WEI2

(1.College of Foundamental Science,Changchun University of Technology,Changchun,130012)

(2.School of Mathematics,Jilin University,Changchun,130012)

We develop a uniaxial optimal perfectly matched layer(opt PML)method for solving the time-harmonic scattering problems by choosing a particular absorbing function with unbounded integral in a rectangular domain.With this choice,the solution of the optimal PML problem not only converges exponentially to the solution of the original scatting problem,but also is insensitive to the thickness of the PML layer for sufficiently small parameterε0.Numerical experiments are included to illustrate the competitive behavior of the proposed optimal method.

uniaxial optimal perfectly matched layer,time-harmonic scattering, convergence

1 Introduction

The first problem to be tackled for the numerical solution of any scattering problem in an unbounded domains is to truncate the computational domain without perturbing too much the solution of the original problem.Perfectly Matched Layer(PML)technique has been developed with this purpose which was introduced by Berenger[1].This method has been applied to different problems(see[2]–[6]).The adaptive PML technique was proposed in [7]for a scattering problem by periodic structures(the grating problem),in[8]for acoustic scattering problem using circular PML domain,and in[9]for scattering problem using rectangular PML domain.

Bermudez and Hervella-Nieto[10]have studied an optimal bounded PML technique by choosing a particular absorbing function with unbound integral.They proved that suchchoice is easy to implement in a finite element method and overcomes the dependency of parameters for the discrete problem.But the PML equations in[10]are of singular coefficients and it is difficult to analyse the convergence of the PML solution.

In this paper we extend the idea of[9]and[10],and choose the PML parameter

where ε0is a sufficiently small positive constant,m ≥ 2,L1and L2are respectively the length and width of computational domain

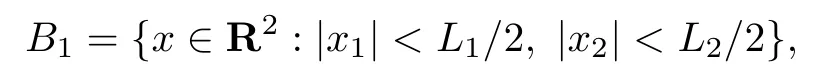
djis the thickness of PML layer,j=1,2.The singularity of coefficents of PML equations disappears.We prove that the PML solutionconverges exponentially to the solution of the original scattering problem u and the following estimation holds:

C＞0 is independent of k,dj,ε0and≤1.From this result we can see that the convergence is insensitive to the thickness of the PML layers for sufficiently small ε0.So the total computational costs can be saved by choosing the thinner PML layer.

2 The Optimal PML Formulation

We study the following problem:

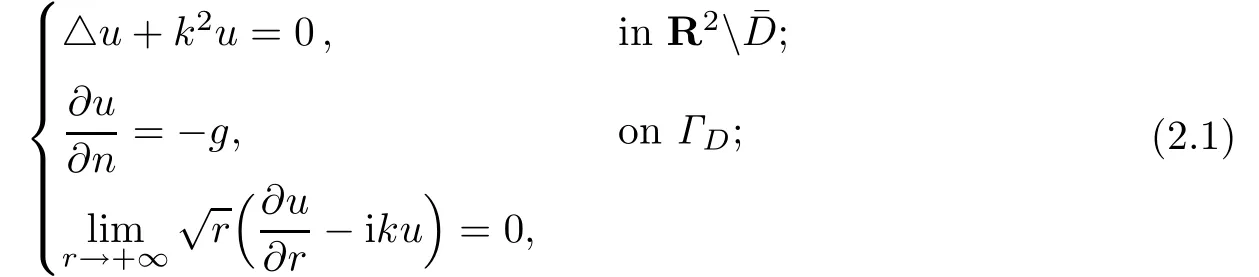
where D ⊂R2is a bounded domain with Lipschitz boundaryΓD,g∈H−1/2(ΓD)is determined by the incoming wave,and n is the unit outer normal vector ofΓD,r=|x|. We assume that k∈Ris a constant.Let D be contained in the interior of the rectangular domain

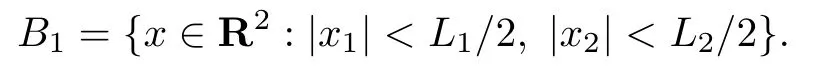
And letΓ1=∂B1,n1be the unit outer normal vector ofΓ1.For given f∈H1/2(Γ1),similar to[9]we introduce the Dirichlet-to-Neumann operator

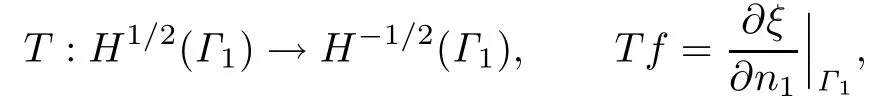
where ξ is the solution of the following problem:

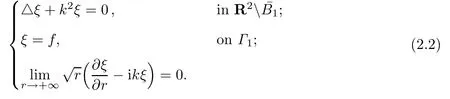
and(·,·)ΓDstands for the inner product on L2(ΓD).The existence of a unique solution of the scattering problem(2.3)is known(cf.,e.g.,[11]and[12]).Then the general theory in [13]implies that there exists a constantµ＞0 such that the following inf-sup condition is satis fi ed:

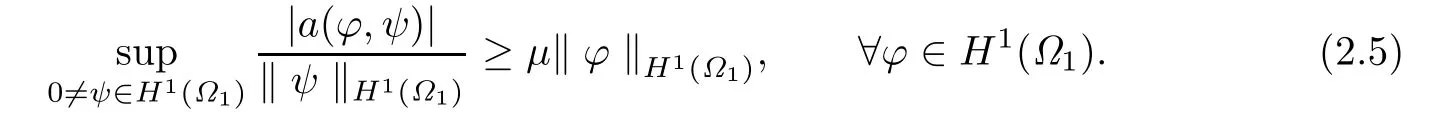
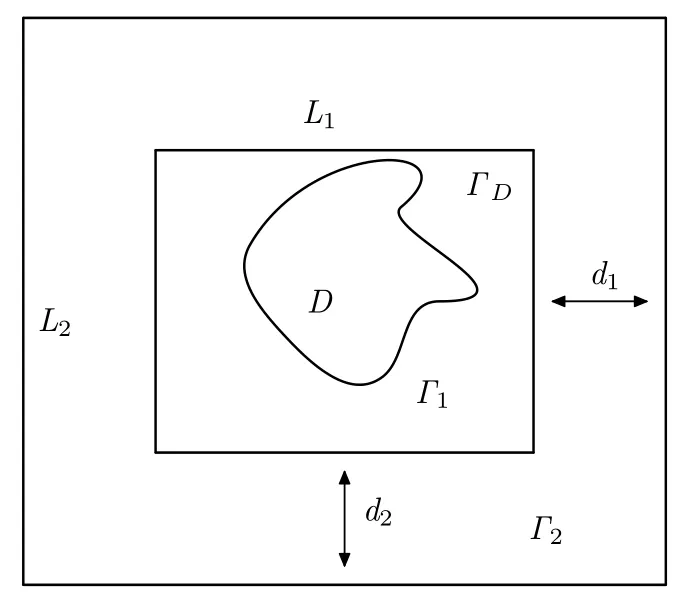
Fig.2.1 The geometric structure of optimal PML layer

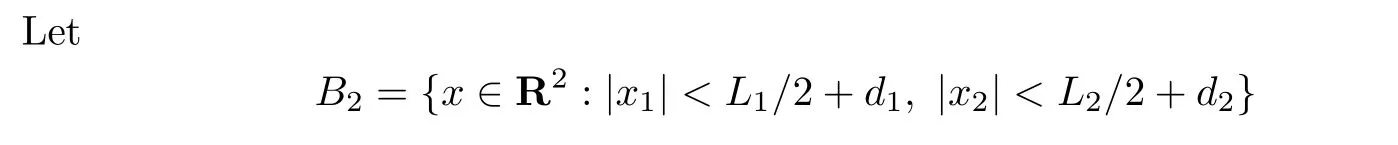
be the rectangle which contains B1,and Γ2=∂B2.We introduce integrable PML parameters γj(xj)such that

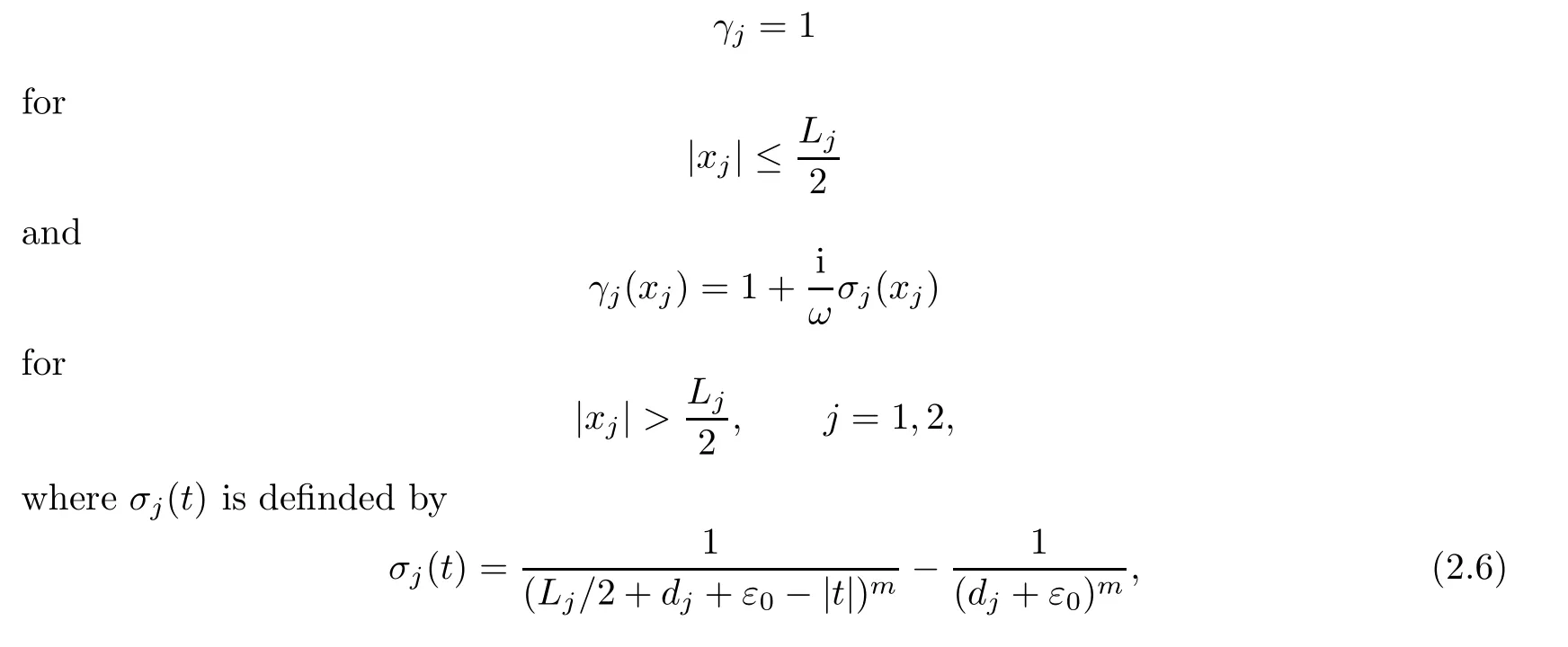
The next section will be devoted to proving the convergence of the solution of(2.16)to the solution of the original scattering problem.

3 Convergence of the PML Solution

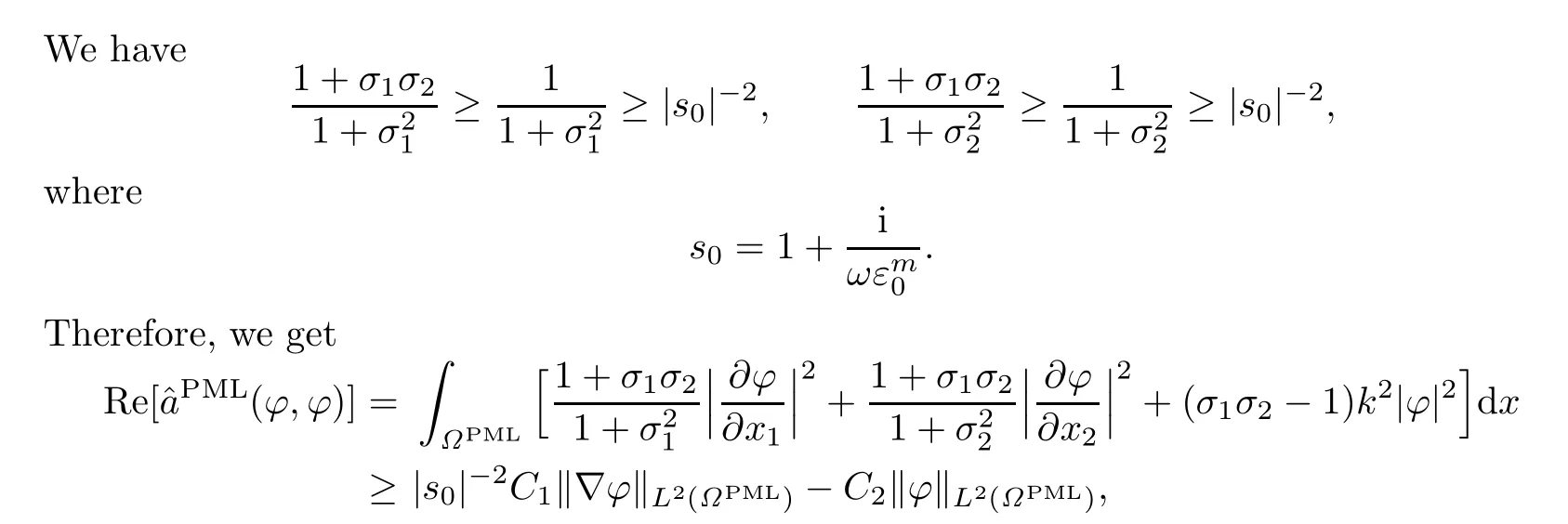
where C1,C2are constants independent of s0.By the Fredholm alternative theorem,we know that(3.2)has a unique solution for every real k except possibly for a discrete set of value of k(see[4]).The general theory in[13]implies that there exists a constantˆC such that

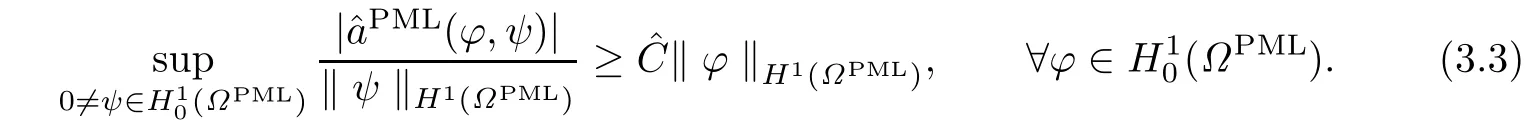
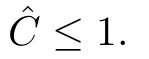
Remark 3.1Generally,the coercivity constantdepends on ε0.We make the technical assumption that

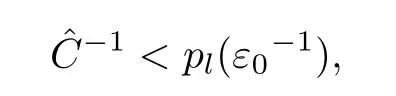
where plis some polynomial of degree l.The assumption makes sense in the convergence of the PML problem,and the numerical experiments indicate that the assumption is reasonable. We need the following result(see[9]).

Thus for sufficiently small ε0,the inequality upon implies=0 inΩ1.This completes the proof.

Theorem 3.3 indicates that the solution of the optimal PML problem converges exponentially to the solution of the original scattering problem.Since the convergence is insensitive to the thickness of the PML layer for sufficiently small ε0,the total computational costs can be saved by choosing the thinner PML layer.

4 Implementation and Numerical Examples

The implementation of the optimal algorithm in this section is based on the PDE toolbox of MATLAB.

In this section,we always take

According to the error estimate in Theorem 3.3,we choose ε0＜0.05 such that

which makes the PML error negligible compared with the finite element discretization errors.

Example 4.1This example demonstrates the accuracy of the optimal PML method for scattering problem of obstacle

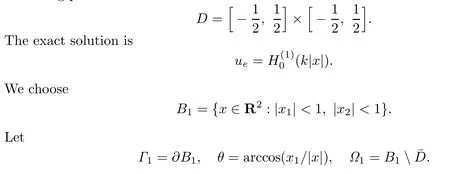
We take the same times of the mesh re fi nements in this example.Fig.4.2 and Fig.4.3 show the real part of the error between exact solution and PML solution onΓ1with different PML layer dj(j=1,2).

These fi gures indicate that the PML method in this paper proposes a new method for solving the scattering problem.From Fig.4.2 and Fig.4.3 we can see that the accuracy is insensitive to the thickness of the PML layer for sufficiently small ε0.

De fi ne the following relative error:

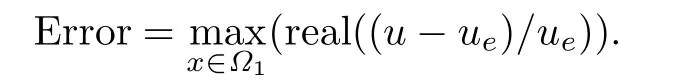
Table 4.1 shows that the accuracy of the optimal PML method is higher.

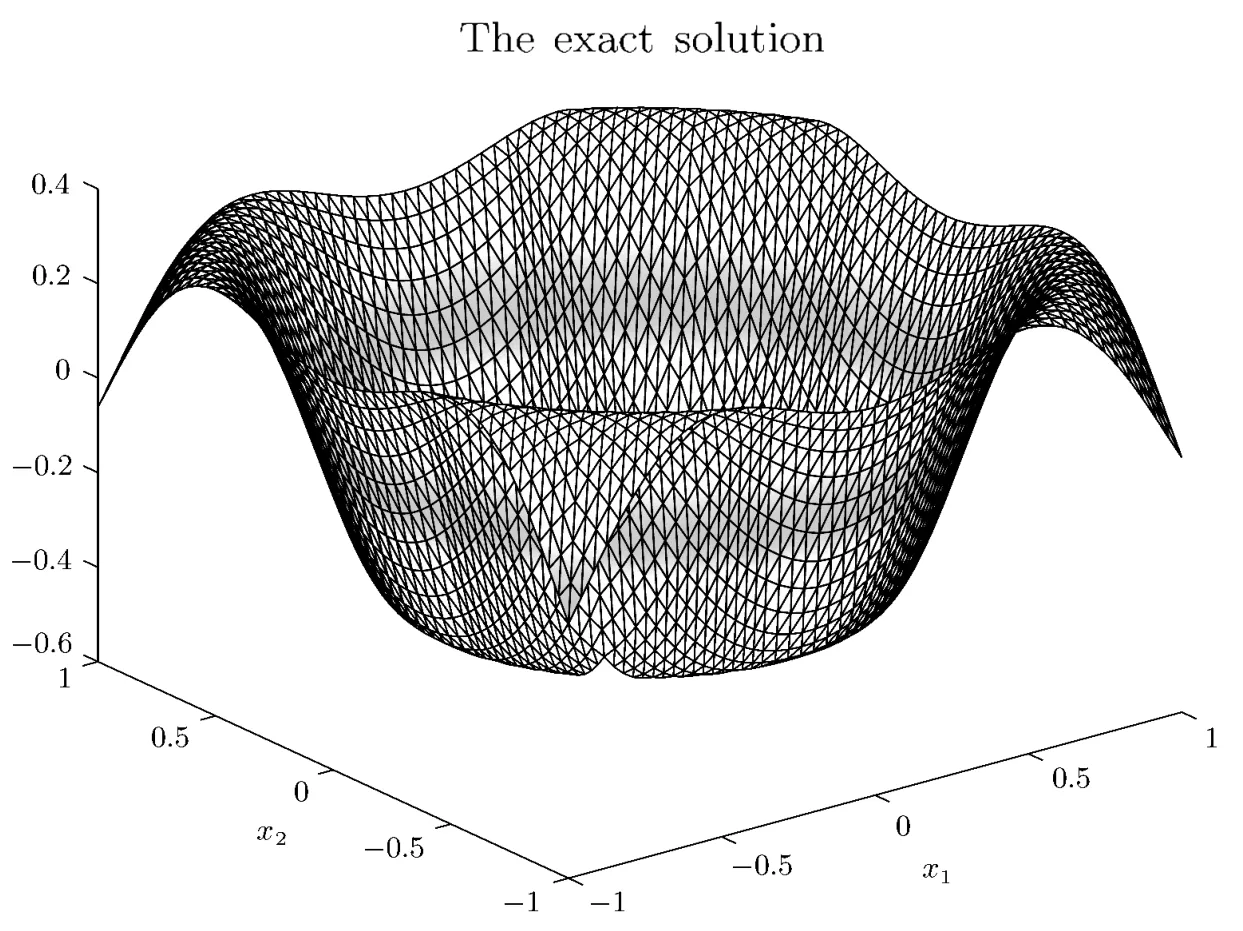
Fig.4.1 The real part of exact solution in Ω1.

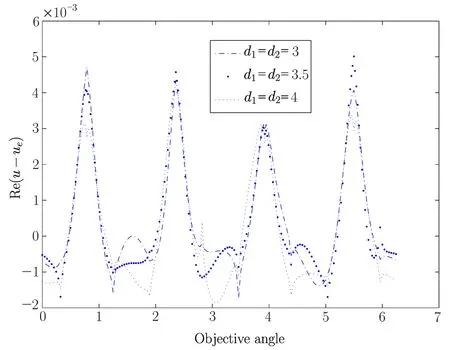
Fig.4.2 The real part of error between PML solution and exact solution as ε0=0.01 on Γ1

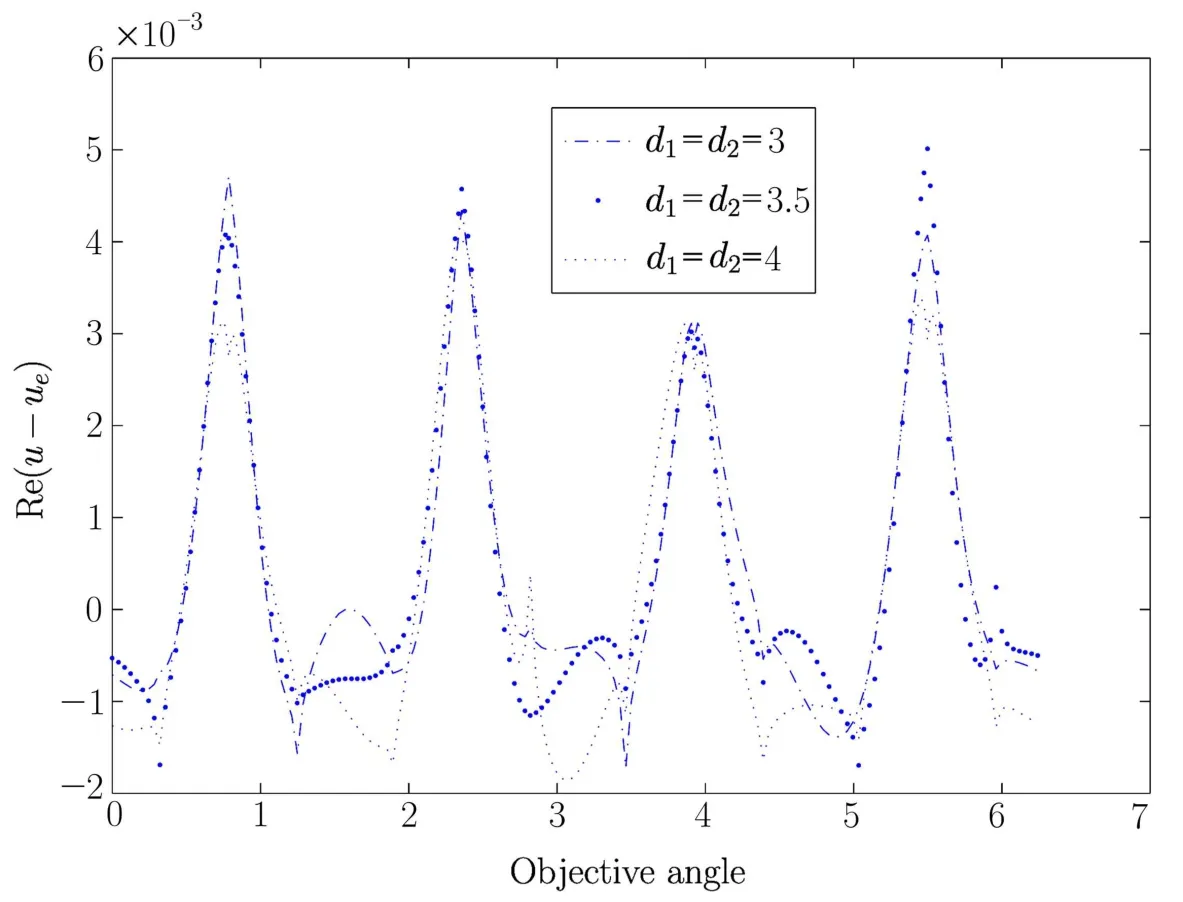
Fig.4.3 The real part of error between PML solution and exact solution as ε0=0.001 on Γ1

Table 4.1 The relative error between PML solution and exact solution in Ω1

Example 4.2In this example,we consider the scattering of the plane wave ui=eikxfrom a perfectly conducting metal.The geometry of the scatter D is taken from[9]as follows.We choose

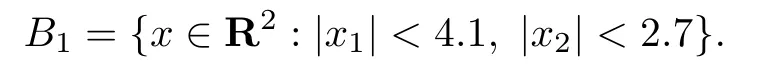
We take the same times of the mesh re fi nements in this example.Fig.4.5 and Fig.4.6 show the real part of the PML solutions onΓ1with different PML layer dj(j=1,2).

From Fig.4.5 and Fig.4.6 we can conclude that the optimal PML method is efficient and accurate to solve the metal scattering problem.

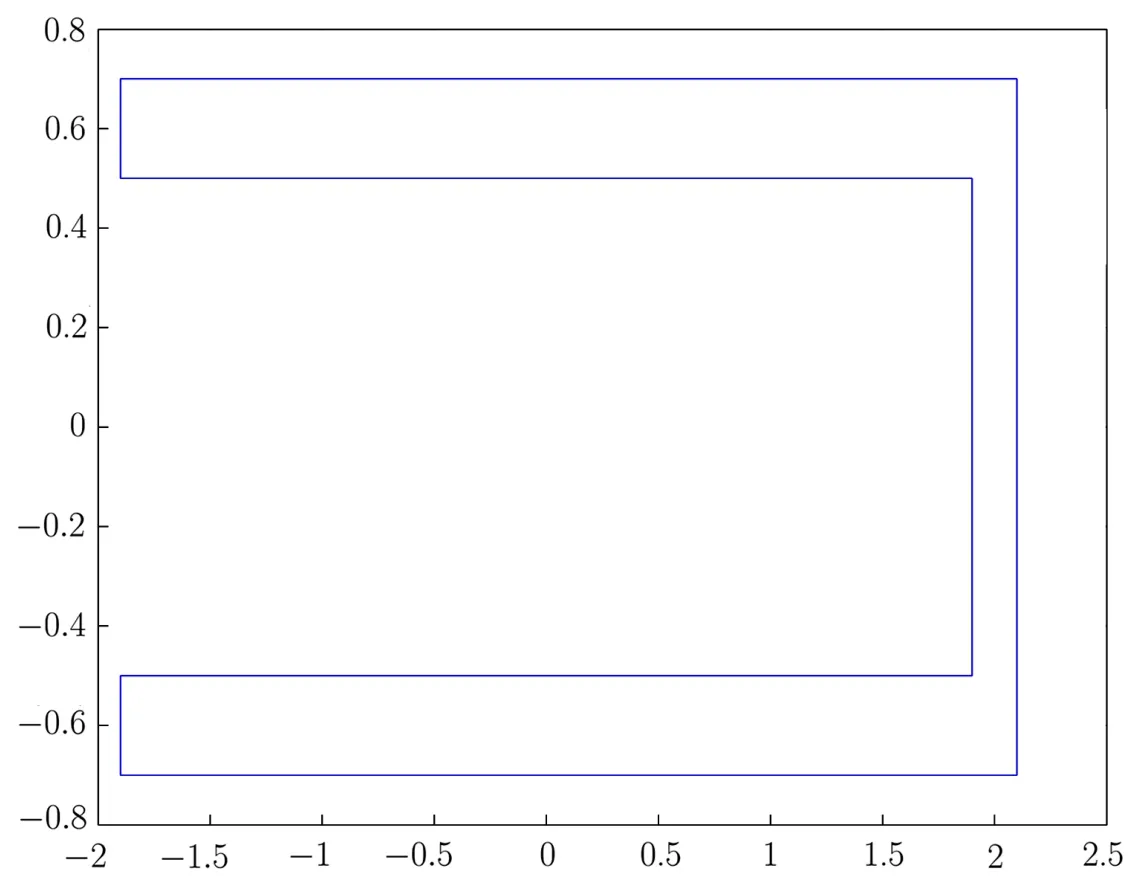
Fig.4.4 The geometry of the scatterer for Example 4.2

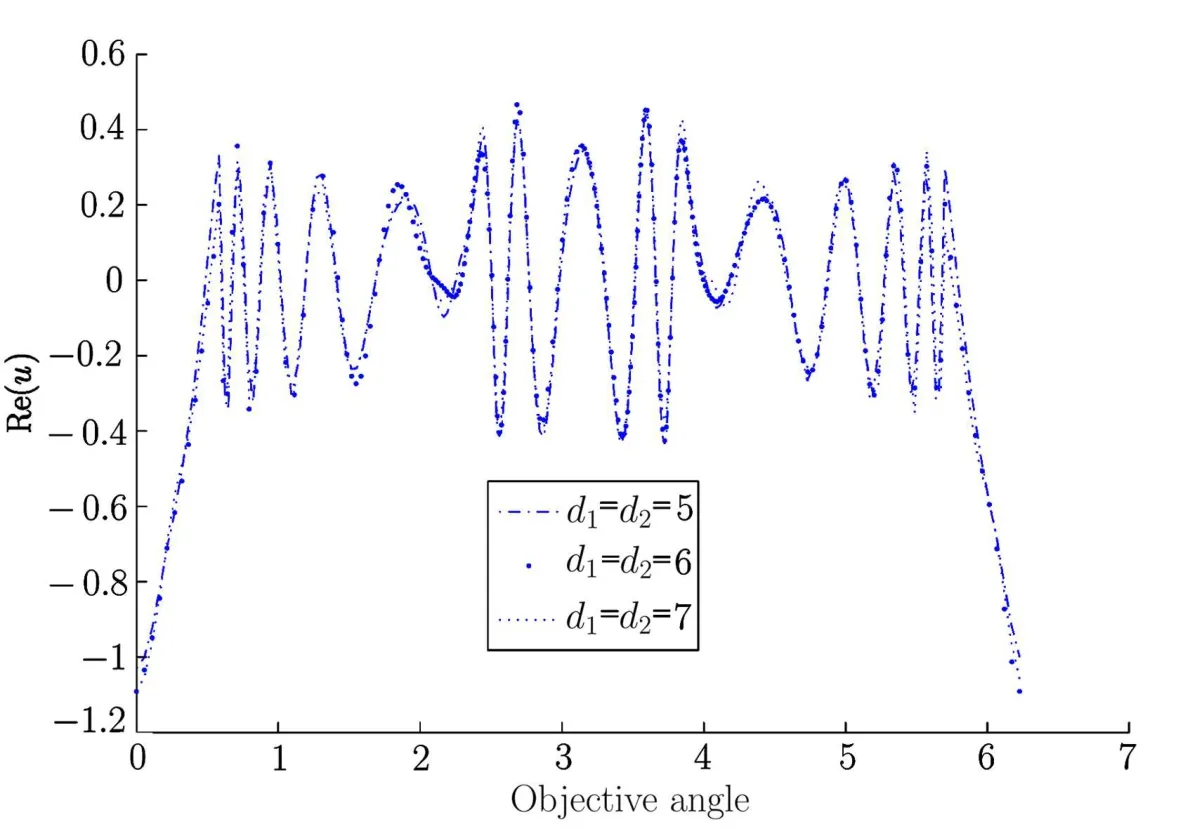
Fig.4.5 The real part of the PML solutions as ε0=0.01 on Γ1

Fig.4.6 The real part of the PML solutions as ε0=0.001 on Γ1

[1]Berenger,J.P.,A perfectly matched layer for the absorption of electromagnetic waves,J. Comput.Phys.,114(1994),185–200.

[2]Teixeira,F.L.and Chew,W.C.,Advances in the theory of perfectly matched layers,in: Chew,W.C.et al.(Eds.),Fast and Efficient Algorithms in Computational Electromagnetics, 283-346,Artech House,Boston,2001.

[3]Turkel,E.and Yefet,A.,Absorbing PML boundary layers for wave-like equations,Appl. Numer.Math.,277(1998),533–557.

[4]Collino,F.and Monk,P.B.,The perfectly matched layer in curvilinear coordinates,SIAM J. Sci.Comput.,19(1998),2061–2090.

[5]Qi,Q.and Geers,T.L.,Evaluation of the perfectly matched layer for computational acoustics,J.Comput.Phys.,139(1998),166–183.

[6]Hu,F.Q.,A stable,perfectly matched layer for linearized Euler equations in unsplit physical variables,J.Comput.Phys.,173(2001),455–480.

[7]Chen,Z.and Wu,H.,An adaptive finite element method with perfectly matched absorbing layers for the wave scattering by periodic structures,SIAM J.Numer.Anal.,41(2003),799–826.

[8]Chen,Z.and Liu,X.,An adaptive perfectly matched layer technique for time-harmonic scattering problems,SIAM J.Numer.Anal.,43(2005),645–671.

[9]Chen,Z.and Wu,X.,An adaptive uniaxial perfectly matched layer method for time-harmonic scattering problems,Math.Theory Methods Appl.,1(2008),113–137.

[10]Bermudez,A.,Hervella-Nieto,L.,Prieto,A.and Rodriguez,R.,An optimal perfectly matched layer with unbound absorbing function for time-harmonic acoustic scattering problems,J. Comput.Phys.,223(2007),469–488.

[11]Colton,D.and Kress,R.,Integral Equation Methods in Scattering Theory,John Wiley and Sons,New York,1983.

[12]McLean,W.,Strongly Elliptic Systems and Boundary Integral Equations,Cambridge University Press,Cambridge,2000.

[13]Babuˆska,I.and Aziz A.,Survey Lectures on Mathematical Foundations of the Finite Element Method,in:Aziz,A.(Ed.),the Mathematical Foundations of the Finite Element Method with Applications to Partial differential Equations,Academic Press,New York,1973,5–359.

[14]Watson,G.N.,A Treatise on the Theory of Bessel Functions,Cambridge University Press, Cambridge,1922.

65N30,78A45,35Q60

A

1674-5647(2010)03-0255-14

date:April 28,2009.

The Major State Research Development Program(2005CB321701)of China,the NSF (10801063)of China.