Affine Locally Symmetric Surfaces in R4∗

HOU ZHONG-HUA AND FU YU

(School of Mathematical Sciences,Dalian University of Technology,Dalian,Liaoning,116024)

Affine Locally Symmetric Surfaces in R4∗

HOU ZHONG-HUA AND FU YU

(School of Mathematical Sciences,Dalian University of Technology,Dalian,Liaoning,116024)

The nondegenerate affine locally symmetric surfaces inR4with the transversal bundle de fi ned by Nomizu and Vrancken[1]have been studied and a complete classi fi cation of the locally symmetric surfaces with fl at normal bundle has been given.

locally symmetric surface, fl at normal bundle,equiaffine normal bundle

1 Introduction

Let M2be a nondegenerate affine surface immersed in the affine spaceR4with the standard affine connection D.An equiaffine structure was found by Nomizu and Vrancken[1]and further investigations showed that the construction leads to natural geometric properties.For the construction of this equiaffine normal plane bundle and the notations used throughout this paper,we refer to[1]and[2].

It is well known that a torsion-free connection∇ is locally symmetric if and only if its curvature tensor satis fies the condition∇R=0.Locally symmetric surfaces in three dimensional affine spaceR3have been studied by a number of authors(see[3]–[6]etc.). In the present paper,we study locally symmetric surfaces in four-dimensional affine spaceR4.Magid and Vrancken[2]showed a complete classi fi cation of all surfaces with fl at induced connection and fl at normal bundle.Based on their work,we classify all the non fl at locally symmetric affine surfaces with fl at normal connection in this paper.Furthermore,we give three examples of locally symmetric surfaces with fl at normal connection,and straightforward computations moreover show that they are not fl at.Precisely,we prove

Theorem 1.1LetM2be a nondegenerate affine locally symmetric surface inR4with fl at normal connection.ThenM2is either fl at or affinely equivalent to an open part of one of the following surfaces:

(1)One of the surfaces

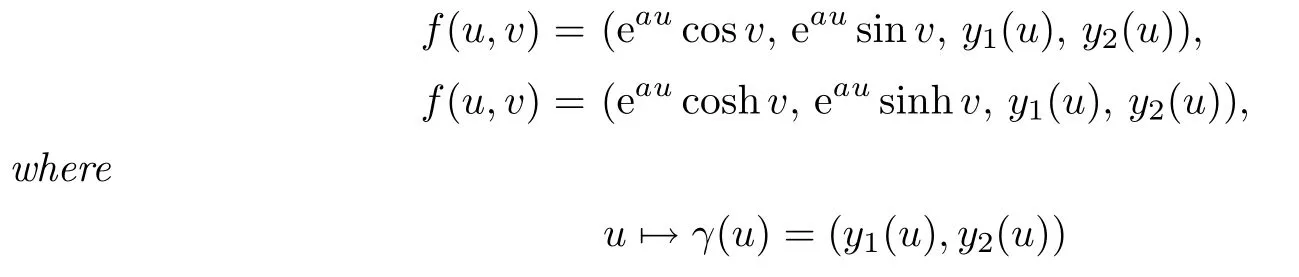
is an arbitrary planar curve parameterized so that

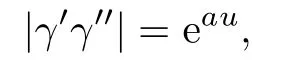
andais a nonzero constant;

(2)The surface

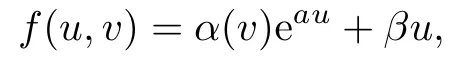
whereαis a curve inR4satisfying

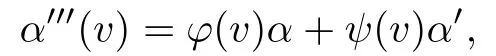
in whichφandψare functions depending only onv,βis a constant vector inR4selected so that

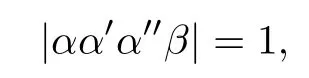
andais a nonzero constant;

(3)The surface

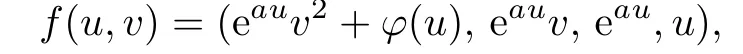
whereφis a function depending onuandais a nonzero constant.

2 Preliminaries

Here,we recall the basic equations for nondegenerate affine surfaces inR4.For more details and proofs,see[1].Let M2be a surface inR4and let u={X1,X2}be a local differentiable frame on a neighborhood U of a point p of M2.We introduce a symmetric bilinear form Guby

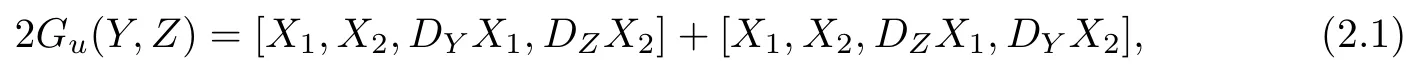
where D is the standard fl at connection and[∗,∗,∗,∗]is the usual determinant onR4.It is easy to see that Guis nondegenerate is independent of the choice of the local frame u. Hence,we call M2nondegenerate if Guis nondegenerate.From now on,we only consider nondegenerate surfaces inR4,following the approaches in[1].If M2is nondegenerate,then the affine metric g is de fi ned by

where the determinant is calculated with respect to the frame u.If g is negative de finite, by interchanging two coordinates inR4,then we can always make g positive de finite.So,if g is de finite,then we always assume that g is positive de finite.

A plane bundle σ is called transversal if,together with the tangent plane,it spans the whole ofR4.Then,by decomposing into a tangential component and a component belonging to σ,we get

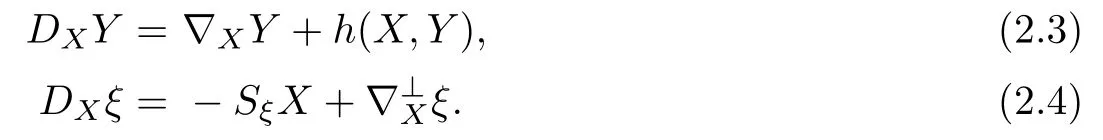
It is straightforward to show that∇is a torsion-free affine connection and Sξis a 1-1 tensor field.We call∇ (resp.∇⊥)the affine connection(resp.the affine normal connection) induced by the normal plane bundle σ.With respect to a local basis{ξ1,ξ2},we can moreover write

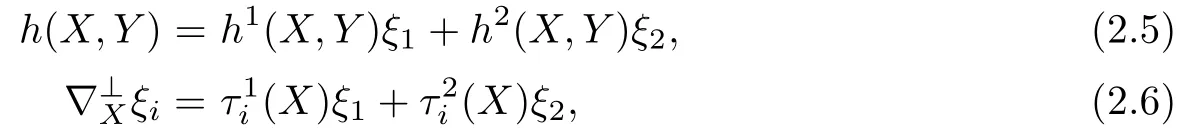
for i=1,2,where h1and h2are symmetric bilinear forms,called the second fundamental forms andare local 1-forms.In order to simplify notation we denote Sξiby Si.

A tangent frame{X1,X2}is called orthonormal if it satis fies

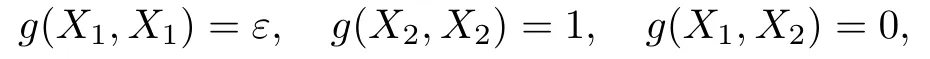
where ε=1 if M2is de finite and ε=−1 if M2is inde finite.

Then,we recall the following lemmas(see[1]):

Lemma 2.1LetMbe a nondegenerate surface inR4with affine metricg.Letu= {X1,X2}be a local orthonormal tangent frame and letσbe the affine normal plane bundle. Then there exists a unique local basis{ξ1,ξ2}ofσsuch that

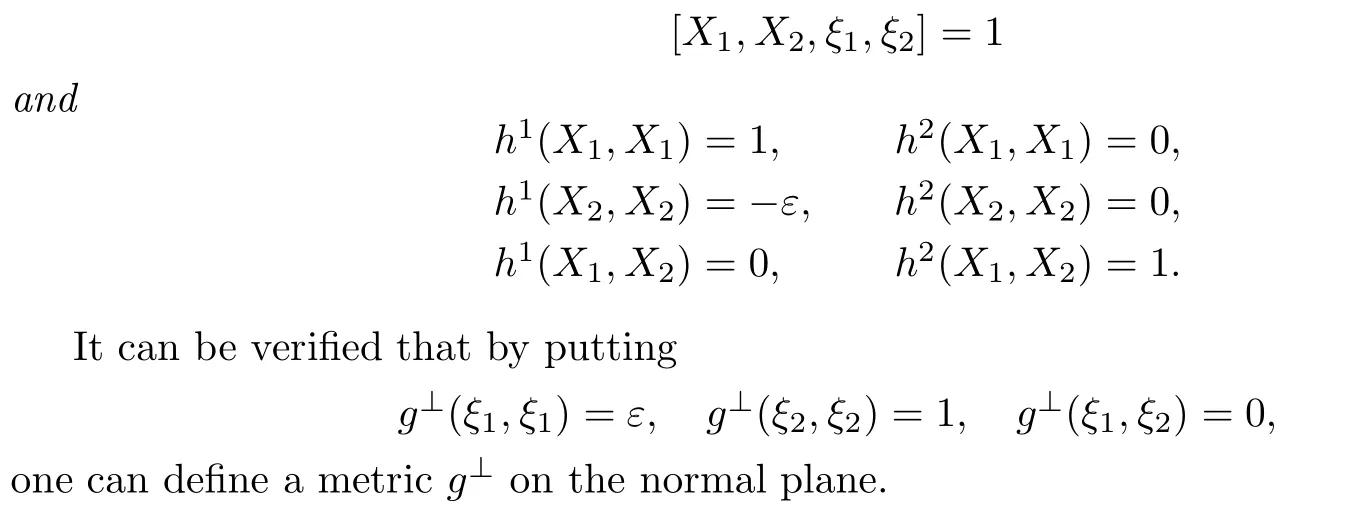
Lemma 2.2LetM2be an inde finite surface.Let{Y1,Y2}be a null frame,i.e.,

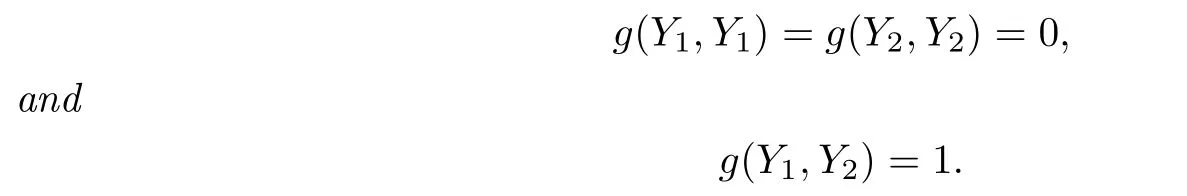
Then there is a unique local basis{η1,η2}of the normal bundleσsuch that

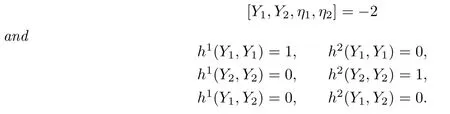
The basic structure equations given by[1]are listed as follows:

According to Gauss equation,the curvature operator R(X,Y)of∇takes the form

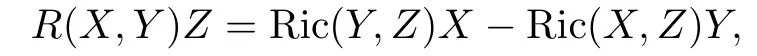
and its covariant derivation is given by

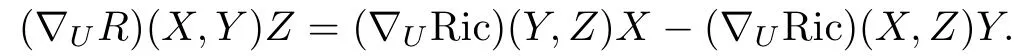
Hence the assumption that∇R=0 is equivalent to the condition∇Ric=0.

For the existence of equiaffine connections,the following proposition is known in[7].Proposition 2.1The following conditions are equivalent:

(1)∇is equiaffine;

(2)Ricis symmetric;

(3)trR(X,Y)=0.

3 Examples of Surfaces with∇R=R⊥=0

First we give some examples of non fl at locally symmetric affine surfaces with R⊥=0.For the examples of fl at affine surfaces with R⊥=0,we refer to[2].

Example 3.1We take a curve γ=(y1,y2)inR2such that

where u is a parameter and a is a nonzero constant.Then we de fi ne a surface inR4by

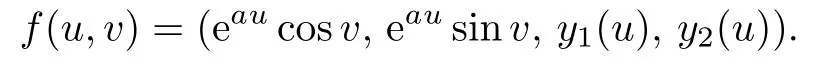
We see from(2.1)and(2.2)that

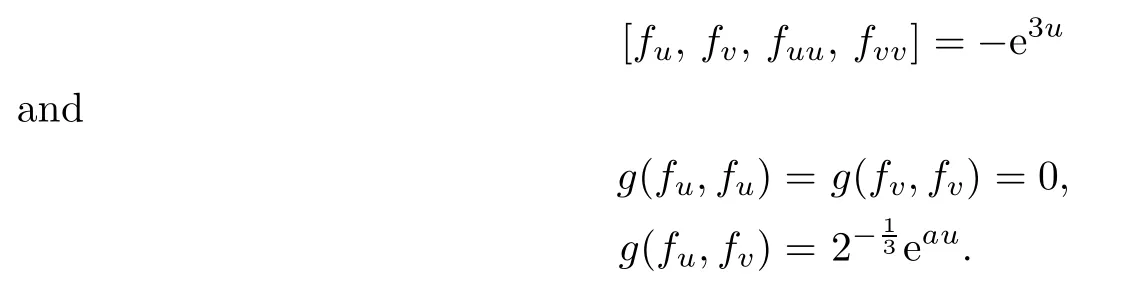
Hence fu,fvare null vector fields.By using

we can also determine that the canonical transversal plane σ is spanned by

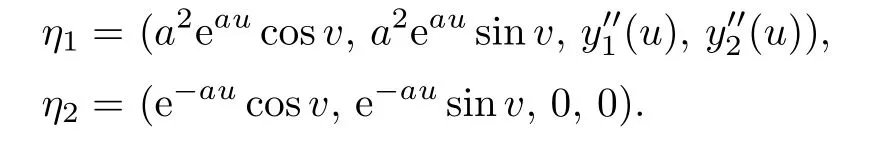
Then the connection induced by the transversal plane determined by η1and η2satis fies

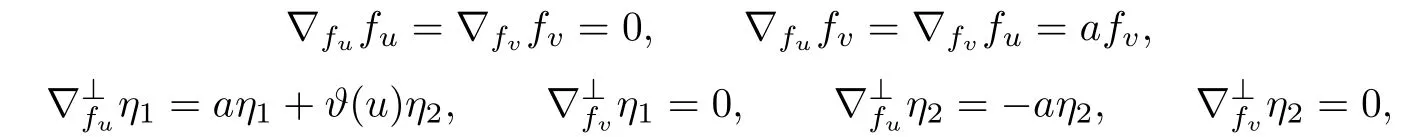
where ϑ is a function depending only on u,and then we get that∇R=0 and R⊥=0,but R0.Similarly it can be shown that the surface de fi ned by

Then η1and η2span the equiaffine normal plane.The connection induced by the transversal plane determined by η1and η2satis fies

4 Proof of Theorem 1.1

In this section,we always assume that M2is a locally symmetric affine surface inR4.

Let

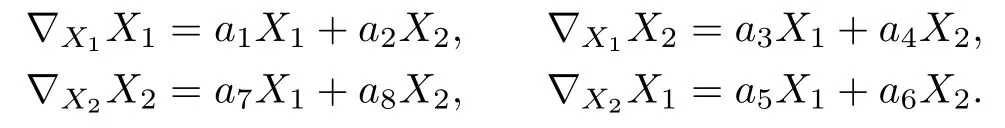
It follows from the Codazzi equations and the choice of equiaffine normal bundle that

where ε=1 if M2is de finite and ε=−1 if M2is inde finite.

Lemma 4.1LetM2be a nondegenerate affine surface inR4with equiaffine transversal bundle.If∇R=0,thendetRic=const.

Proof.Now,we write

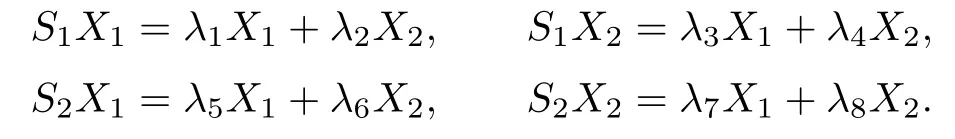
From the Gauss equation(2.7),the curvature tensor R of∇is given by

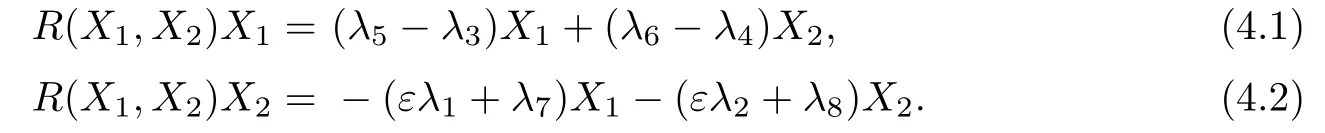
By Proposition 2.3,∇is equiaffine implies

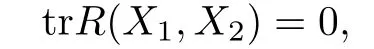
and hence we have

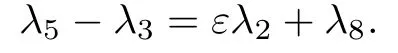
Then,the Ricci tensor takes the values

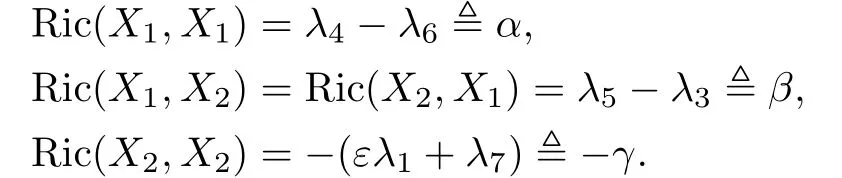
Since∇R=0 is equivalent to the condition∇Ric=0,we calculate the components with respect to{X1,X2}by

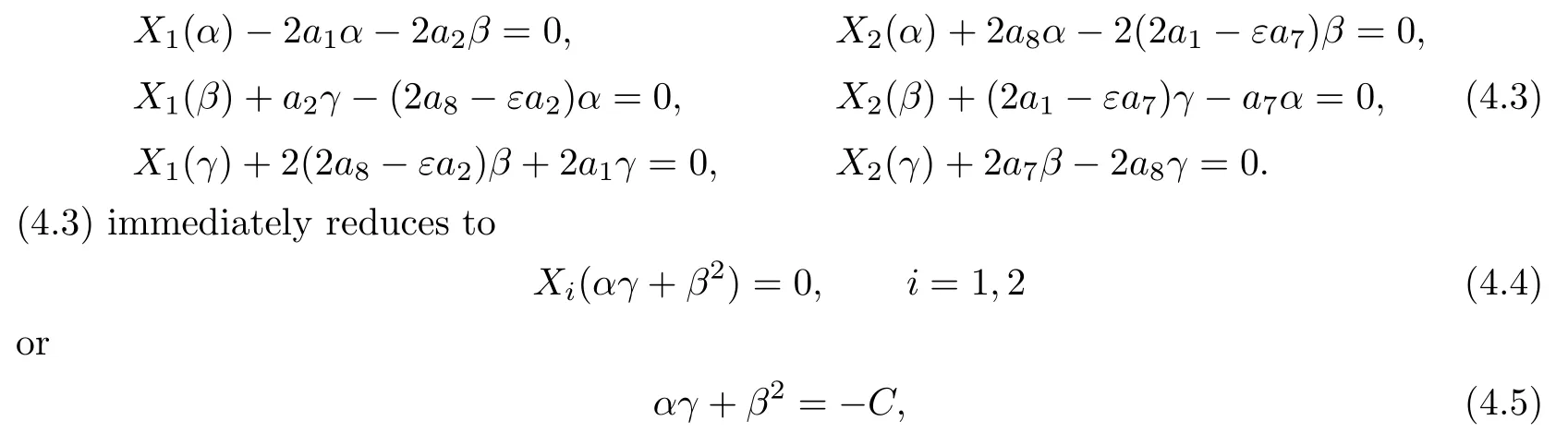
where C is a constant.Hence we have detRic=C.

In order to calculate easily,we state the following lemma.It follows from the Codazzi equations and the choice of equiaffine transversal bundle(see also[8]).

Lemma 4.2LetM2be an inde finite surface inR4and{Y1,Y2}be a null basis onM2. Denote

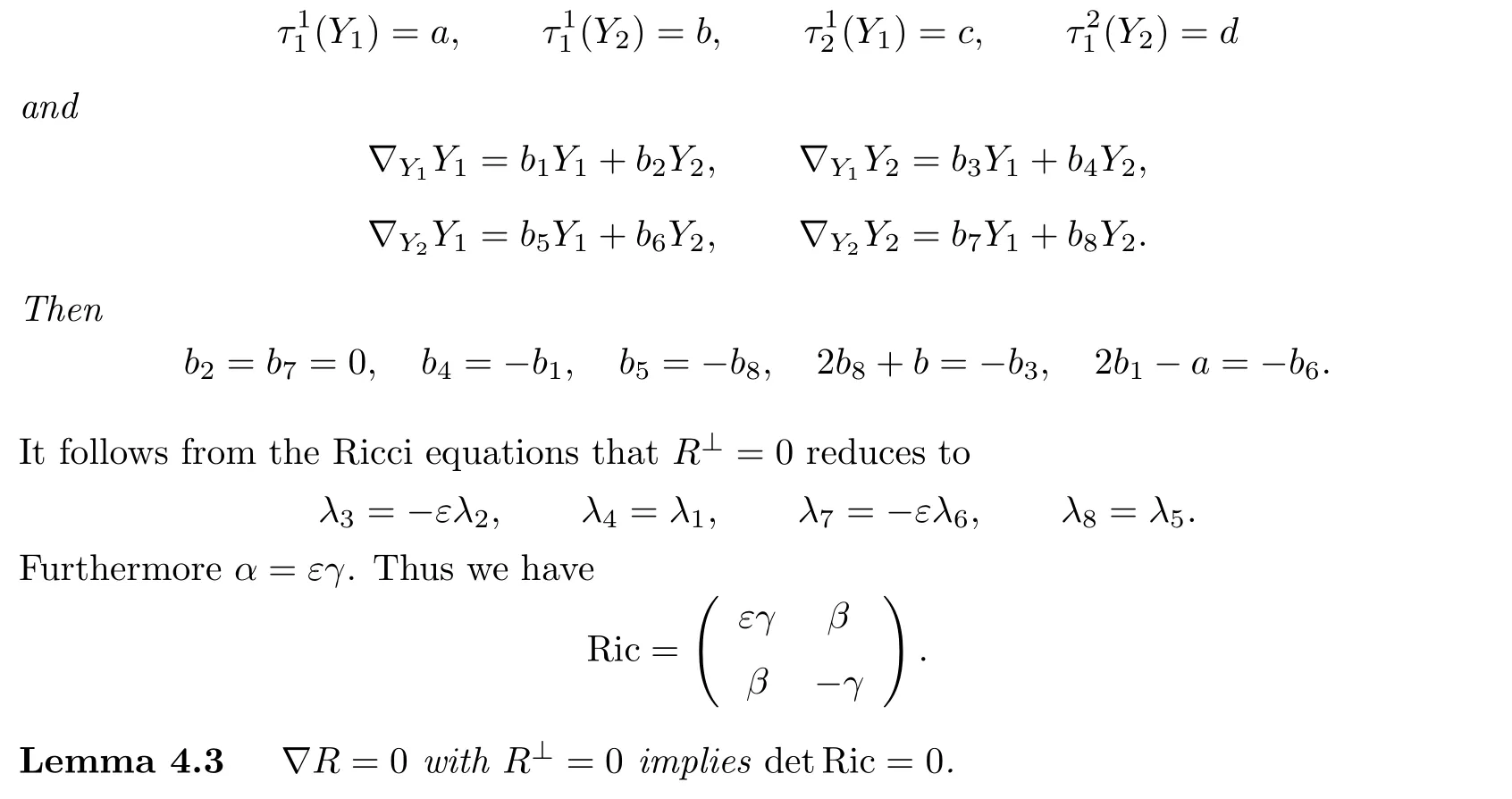
Proof. Firstly,we consider the de finite case,i.e.,ε=1.After making an orthogonal transformation,the Ric matrix

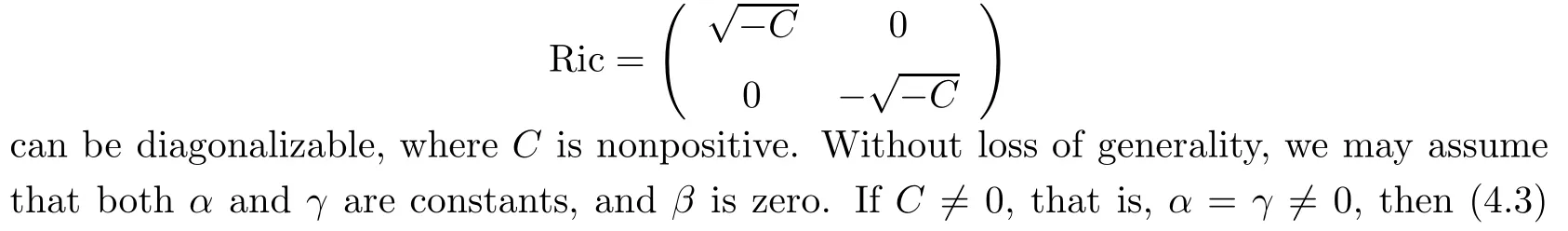
The integrability condition of the last system is satis fi ed trivially.We have[Y1,ρY2]=0.So if we denote the immersion of M2inR4by f,then we get that there exists local coordinate (u,v)such that fu=Y1and fv=ρY2.Therefore,the function ρ is given by ρ=C1eau, where C1is a nonzero constant.

Applying the Gauss formulas and Weingarten formula,we obtain that

This is a linear differential equation,and clearly a constant function is a solution.Therefore, there exist three constant vectors B3,B4,B5such that the general solution of(4.16)can be written as

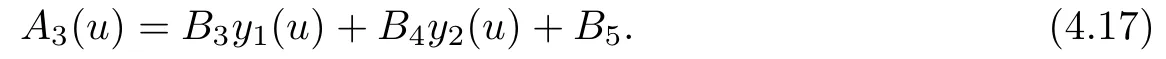
Since our surface is linearly full inR4,by applying an affine transformation,we may assume that

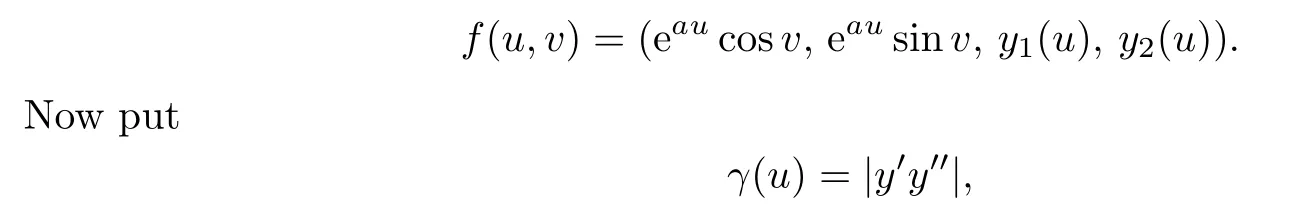
where“′”denotes the derivative with respect to u.Then(4.16)implies that

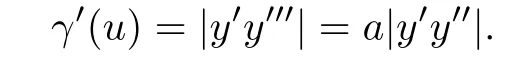
Hence there exists a constant B6such that

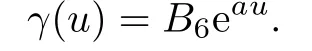
By applying another affine transformation,if necessary,we may assume that B6=1. If C2＜0,similarly,then we get

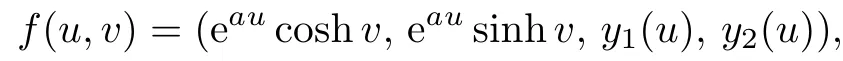
where a is a constant.This gives the surface of type(1).

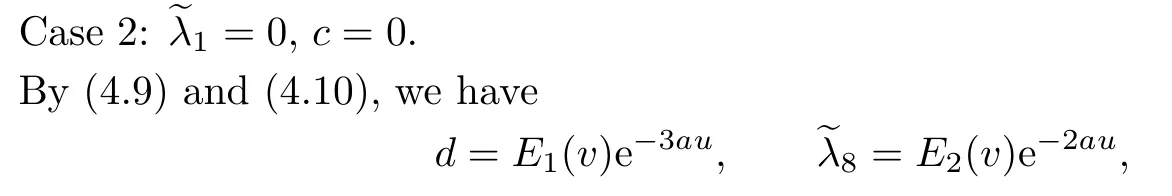
where E1and E2are functions depending only on v.Thus

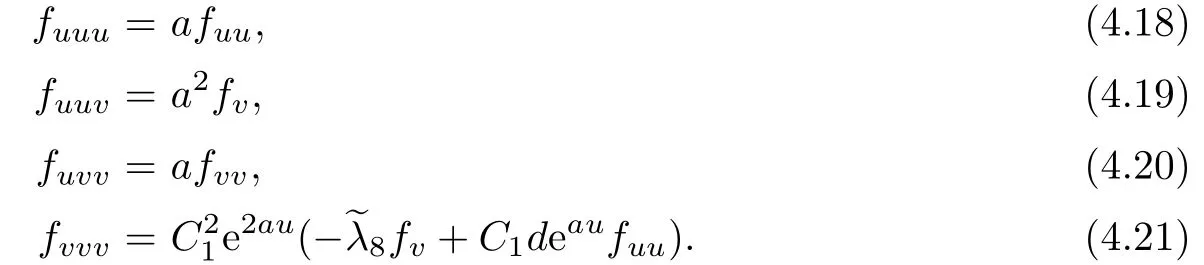
From(4.18)we get fuu=D1(v)eau,and therefore the immersion can be written as

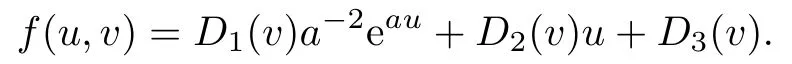
Then(4.19)and(4.20)are reduced to

and thus both D2(v)and D3(v)are two constant vectors.Furthermore,(4.21)implies

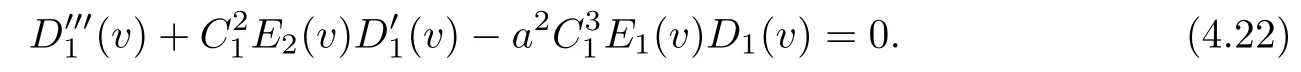
By applying an affine transformation,we may assume that

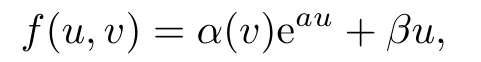
where β is a constant vector inR4.Since(4.22)is a third-order linear differential equation, we have that α is a curve included in a hyperplane inR4and satis fies

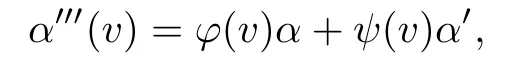
where φ and ψ are functions depending on v.Clearly,α,α′,α′′are linearly independent inR4,and therefore we have

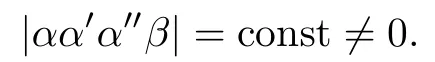
This gives the surface of type(3).

The proof of Theorem 1.1 is thus completed.

AcknowledgmentThe second author would like to express his sincere gratitude to Professor Luc Vrancken for his valuable advice.

[1]Nomizu,K.and Vrancken,L.,A new equiaffine theory for surfaces in R4,Internat.J.Math., 4(1993),127–165.

[2]Magid,M.and Vrancken,L.,Flat affine surfaces in R4with fl at normal connection,Geom. Dedicata,81(2000),19–31.

[3]Slebodzinski,W.,Sur quelques problemes de la theorie des surfaces de l’espace affine,Prace Mat.Fiz,46(1939),291–345.

[4]Dillen,F.,Locally symmetric complex affine hypersurfaces,J.Geom.,33(1988),27–38.

[5]Opozda,B.,Locally symmetric connections on surfaces,Results Math.,20(1991),725–743.

[6]Jelonek,W.,Affine locally symmetric surfaces,Geom.Dedicata,44(1992),189–221.

[7]Nomizu,K.and Sasaki,T.,Affine differential Geometry:Geometry of Affine Immersions, Cambridge University Press,New York,1994.

[8]Verstraelen,L.,Vrancken,L.and Witowicz,P.,Inde finite affine umbilical surfaces in R4,Geom. Dedicata,79(2000),109–119.

53A15

A

1674-5647(2010)03-0269-11

date:Feb.23,2009.