模糊PID控制性能仿真分析

李建春,李相白

(云南驰宏锌锗股份有限公司,云南曲靖655000)

模糊PID控制性能仿真分析

李建春,李相白

(云南驰宏锌锗股份有限公司,云南曲靖655000)

通过对目前流行的模糊 PID控制方法的总结,研究了各种控制结构,使用Matlab的仿真工具Simulink的Fuzzy模块进行仿真分析,比较其各自的优缺点,得出规律性结论,为模糊PID控制系统设计提供帮助.

模糊控制;PID;仿真

模糊控制系统是以模糊集合论、模糊语言变量和模糊逻辑推理为基础的一种计算机数字控制技术.模糊控制系统主要是模拟人的思维、推理和判断的一种控制方法,它将人的经验、常识等用自然语言的形式表达出来,建立一种适用于计算机处理的输入输出过程模型,是智能控制的一个重要研究领域.从信息技术的观点来看,模糊控制是一种基于规则的专家系统.从控制系统技术的观点来看,模糊控制是一种普遍的非线性特征域控制器[1-4].

PID控制是现实中使用最广泛的控制算法,而且有着相当优越的控制性能.结合模糊控制和PID控制优点的模糊PID控制算法越来越受到人们的重视.

Matlab的Simulink工具箱是一个对动态系统进行建模、仿真和分析的软件包.Simulink提供了一种图形化的交互环境,只需用鼠标拖动的方法便能迅速地建立起系统框图模型,甚至不需要编写一行代码.利用 Simulink进行系统的建模仿真,其最大优点是易学、易用,并能依托Matlab提供的丰富的仿真资源.本文利用Matlab的仿真工具Simulink的Fuzzy模块进行模糊PID仿真分析研究.

1 模糊控制基本原理和 PID调节器

模糊控制的基本原理如图1所示.它的核心部分是模糊控制器,主要包括输入量的模糊化、模糊推理和清晰化3部分.

图1 模糊控制的基本原理图

按偏差的比例、积分和微分进行控制的调节器,简称PID调节器.它是工业领域应用最为广泛和成熟的控制方法.典型的闭环PID控制系统结构如图2所示.

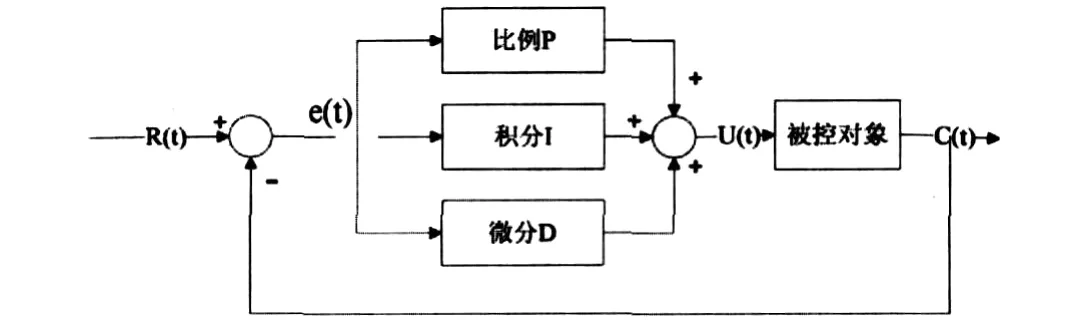
图2 典型的闭环PID控制系统结构

PID调节器参数对控制系统性能的影响为:

(1)比例参数 Kp:实时成比例地反映控制系统的偏差.偏差一旦产生,调节器立即作用以减少偏差.Kp增大,系统的稳态误差将减少,响应加快,但过大的 Kp会使系统趋于不稳定.

(2)积分参数 Ki:消除系统的稳态误差(静差),提高控制系统的无差度,Ki越大,系统动态响应越慢.

(3)微分参数 Kd:反映误差变化率,产生超前的校正作用.

2 模糊PID控制结构及仿真分析

在以下分析中,控制对象使用二阶惯性延时系统,延时时间为3 s.控制输入为阶跃输入,数值设为0.5.模糊控制都使用双入单出模型,量化档数都取7档,隶属度函数都取三角函数,控制规则为49条.输入的论域都为-6到6.

2.1 引入积分因子的模糊PID控制器

2.1.1 具有积分项的模糊控制器

具有积分项的模糊控制器结构框图如图3所示,积分环节加在误差输入量的模糊化之前和模糊控制器输出量的解模糊之后.这种结构在一定程度上可减少系统余差,但无法保证消除系统极限环振荡现象,尤其是当 K2、K3取的过大时,系统可能出现不稳定.这种结构设计目前应用较少,其Simulink仿真框图如图4所示.

由试验得知,控制参数 K1、K2、K3难以调节,得不到较为理想的控制波形图.该控制方法很少使用.

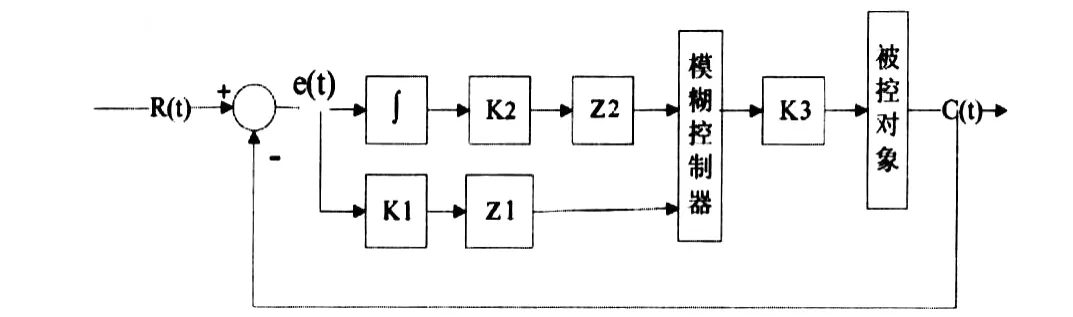
图3 有积分项的模糊控制器结构框图

图4 仿真框图

2.1.2 混合型模糊PID控制器

这种控制器由一个常规积分控制器和一个二维模糊控制器相并联而成.两者的输出作为混合型模糊PID控制器的总输出,使系统成为无差模糊控制器.其控制框图如图5所示.

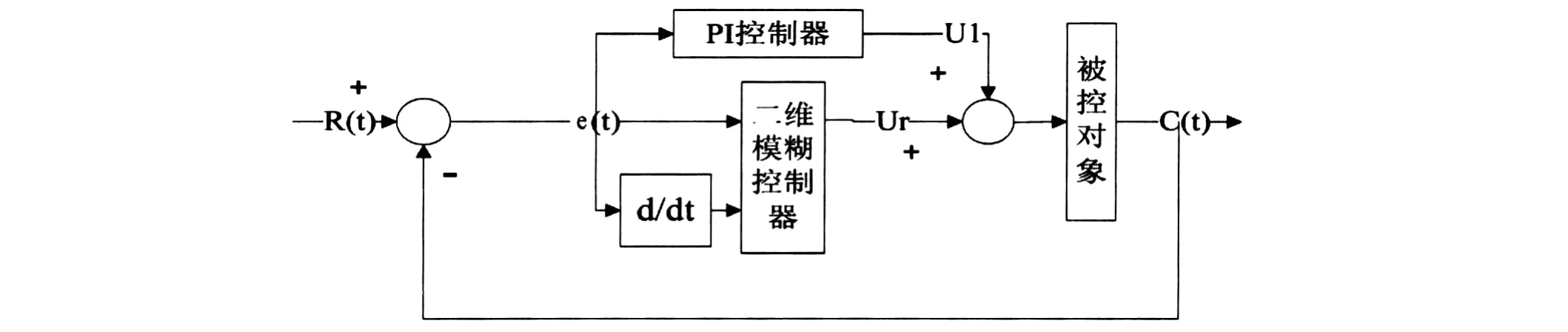
图5 混合型模糊PID控制器

混合型模糊PID控制器Simulink仿真框图如图6所示.依据图 6进行分析,其中 Kp=0.6,Ki=0.1,输入取常数值.分别改变 K1、K2、K3,控制效果如表1所示.

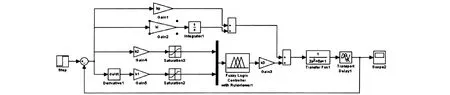
图6 混合型模糊PID控制器仿真框图

表1 混合型模糊PID仿真参数及结果统计

由以上分析可见:

(1)在误差变化率量化档数、误差和控制量比例因子一定的情况下,当 K1选择较大时,误差变化率的基本论域缩小,增大了误差变化率的控制作用,抑制了系统超调,但是过渡时间变长.

(2)在误差量化档数、误差变化率和控制量比例因子一定的情况下,当 K2选择较大时,误差的基本论域缩小,增大了误差的控制作用;系统上升时间缩短、超调量增加、系统响应时间变长.

(3)在控制量化档数、误差和误差变化率一定的情况下,当 K3选择较大时,控制量的基本论域扩大,增大了控制量的控制作用,加快了系统响应;但是过大的控制量因子会导致系统大的超调.

2.2 FUZZY-PID开关切换控制

FUZZY-PID开关切换控制原理如图7所示.该控制方式的基本思想是在大偏差范围内采用Fuzzy控制,在小偏差范围内转成 PID控制,即保留了 Fuzzy控制动态响应快的优点,又具有PID控制稳态精度高的优点.

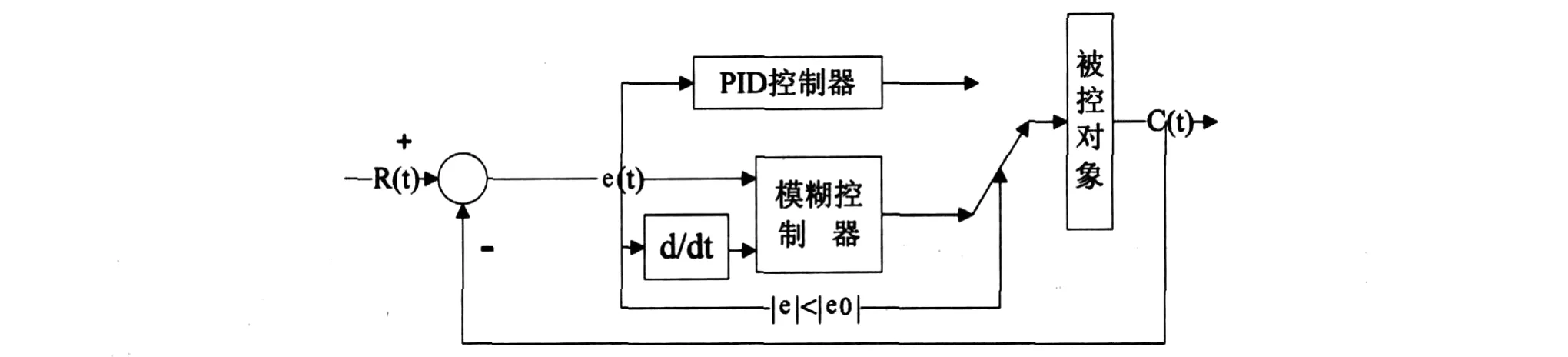
图7 FUZZY-PID开关切换控制原理图

各种开关切换方式下的切换时刻选择如下[5-6]:

(1)常规切换方式:误差阀值切换,即设定当|e|<|e0|时,由模糊控制切换为PID控制方式.该方法的缺点是|e0|的选取即何时切换,以及切换瞬间的扰动问题.

(2)加权平均切换方式,也称误差区间切换方式:预先把误差分为3个区域,当|e|>|e2|时,采用模糊控制方式;当|e|<|e1|时,采用 PID控制方式;当|e1|<|e|<|e2|时,输出为2种控制方式的加权平均.采用加权平均切换方式可以实现光滑无扰切换,是实际应用中最常用的切换方法.该方法的缺点是3个区间的划分,带有一定的主观因素.

(3)模糊规则切换方式:控制规则定义为Ifeisz1 andecisz2,thenUisUpidelseUisUfuzzy. 其中 Upid和Ufuzzy分别是 PID控制器和模糊控制器的输出,z1和z2是模糊切换规则的隶属度函数,改变隶属度形状可以获得不同的控制强度.

当某一采样时刻误差和误差变化率分别为e(k)和ec(k)时,经过上述规则的模糊推理运算,得到 PID控制器和Fuzzy控制器的输出强度系数,分别为 wpid和 wfuzzy,则有:

最终控制器的输出采用加权平均:

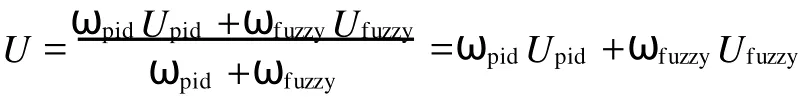
本例中使用常规切换方式,其Simulink仿真结构图如图8所示,其中选择|e0|=0.1.

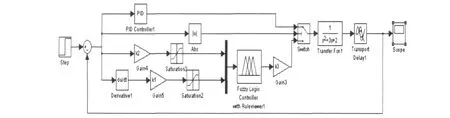
图8 FUZZY-PID开关切换控制仿真结构图

分别改变 K1、K2、K3,得到相应的控制波形图, 如图9所示,对应的数据结果统计如表2所示.

图9 修改 K1、K2、K3的 FUZZY-PID控制波形图

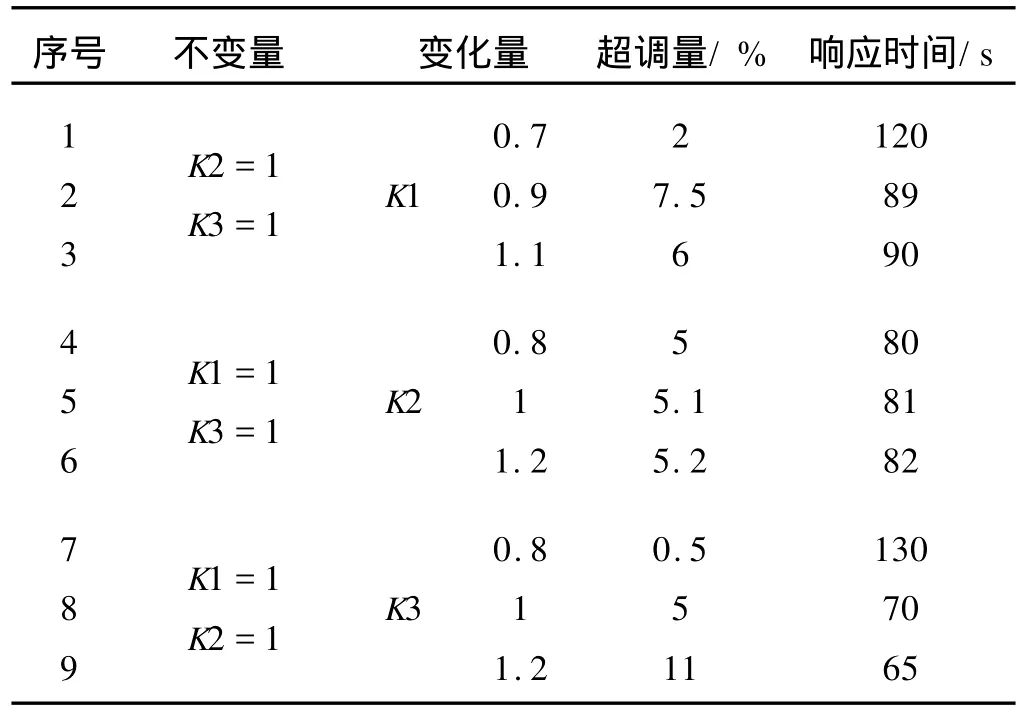
表2 FUZZY-PID开关切换控制仿真参数及结果统计

由表2可以看出,Fuzzy-PID开关切换控制中参数 K1、K2、K3对系统的影响效果与混合型模糊 PID控制的效果基本上一样,但相对于后者,其更容易实现调节控制.

2.3 模糊自适应整定PID控制

常规PID控制器具有计算量少、实时性好等优点,在工程领域得到广泛应用.其主要缺点是参数修改不方便,不能进行自整定.为此出现了各种自适应PID控制方法,目前较多的是采用对被控对象进行在线辨识,然后根据一定的控制要求或目标函数对PID控制器的3个参数(Kp、Ki、Kd)进行在线调整.这种方法建立在被控对象的精确数学模型基础上,有一定局限性,尤其是当被控对象具有非线性、参数时变性以及模型不确定性时,辨识方法往往不一定有效[7-10].模糊自适应整定PID控制器是利用模糊控制规则对PID参数进行在线修改的一种自适应方法,它以误差e和误差变化ec作为输入,可以满足不同时刻e和ec对PID参数自整定的要求.其基本结构图如图10所示.

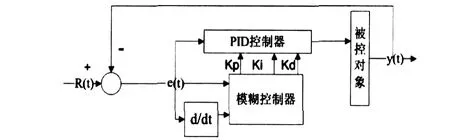
图10 PID参数自整定结构图

PID参数自整定的实现思想是:先找出PID 3个参数与偏差e和偏差变化ec之间的模糊关系,制成模糊控制规则表,在运行中通过不断检测e和ec的值,再根据模糊控制规则表进行模糊推理来对3个参数进行在线修改,以满足不同e和ec对控制器参数的不同要求,从而使被控对象具有良好的动、静态性能,而且计算量小,易于单片机实现.

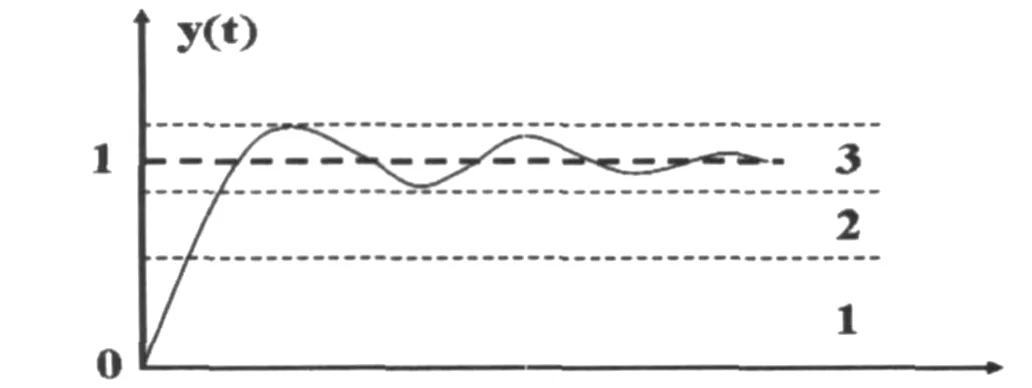
图11 输出响应曲线

根据参数 Kp、Ki、Kd对系统输出特性的影响,可归纳出在一般情况下被控过程对3个参数自整定的要求[11]:

(1)当|e|较大时(图11输出响应曲线的1区),为了加快系统的响应速度,并避免因开始时偏差e的瞬间变大可能引起微分过饱和而使控制作用超出许可范围,此时应取较大的 Kp和较小的 Kd;同时为了防止积分饱和,避免系统响应出现较大的超调,此时应去掉积分作用,取 Ki=0.

(2)当|e|和|ec|为中等大小时(图11输出响应曲线的2区),为使系统响应的超调减少,Kp、Ki、Kd都不能取大,应取较小的 Ki值,Kp和 Kd的大小要适中,以保证系统的响应速度.

(3)当|e|较小时(图11输出响应曲线的3区),为使系统具有良好的稳态性能,应增大 Kp和 Ki的值;同时为避免系统在设定值附近出现振荡,并考虑系统的抗干扰能力,应适当选取 Kd值.

(4)根据上述3条自整定要求设计模糊控制器,输入为e和ec,输出为 Kp、Ki、Kd,就可以实现参数的模糊自适应调整.

建立模糊自适应整定PID控制仿真结构图,如图12所示.模糊自适应整定PID控制仿真参数及结果统计如表3所示.

图12 模糊自适应整定PID控制仿真结构图

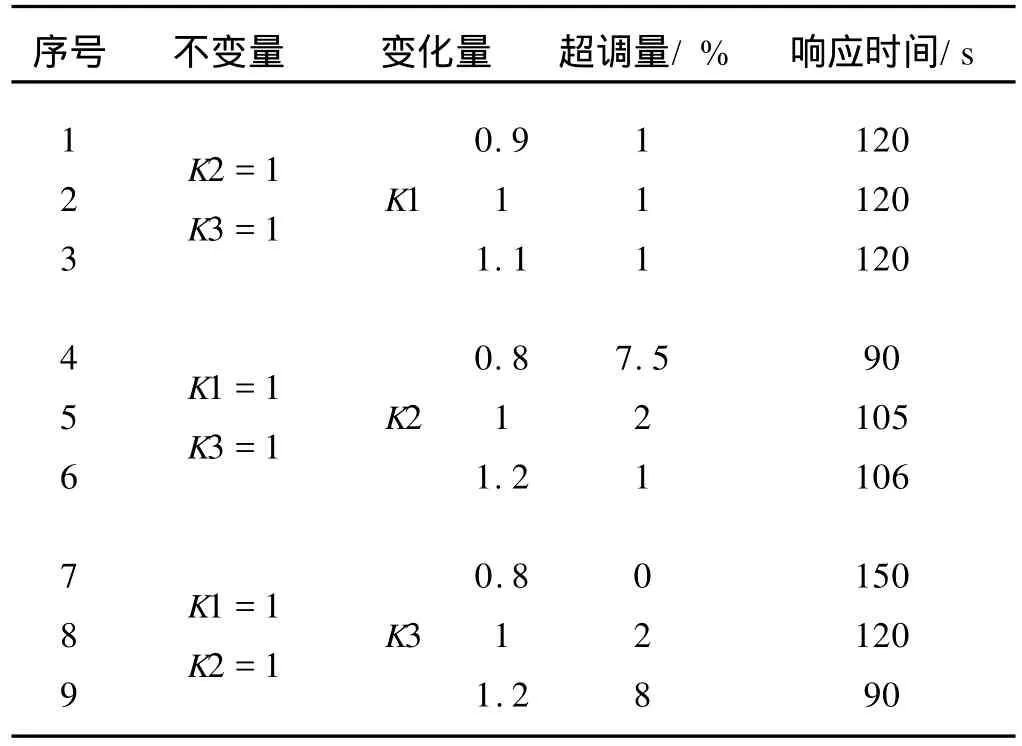
表3 模糊自适应整定PID控制仿真参数及结果统计

由表3可以看出,在模糊自适应整定 PID控制中,修改误差变化率的比例因子 K1,控制性能基本上没有多少变化;当误差的量化因子变化增大时,超调量减小,而响应时间则增大,但是变化比较缓慢;控制量因子增大,会使超调量增大,系统响应时间减小;控制性能对控制量因子的反应比较敏感.

3 结 语

通过分析可以看出,模糊PID控制对于控制对象不需要清楚了解.其中 K1、K2、K3的变化对于控制性能的影响基本一样,只是在敏感性上有所不同.

(1)当 K1选择较大时,误差变化率的基本论域缩小,增大了误差变化率的控制作用,抑制了系统超调,但是过渡时间变长;当误差的量化因子 K2变化增大时,超调量减小,而响应时间则增大;控制量因子 K3增大会使超调量增大,系统响应时间减小.

(2)FUZZY-PID开关切换控制的计算量小,FUZZY-PID开关切换控制PID环节的整定需要对被控对象有一定的了解.不过即使有些差错,由于阀值|e0|的存在,也不会出现太多的偏差.但如果参数设置不理想,会引起输出振荡.

(3)模糊自适应整定 PID控制计算量相对较大,但是对于控制对象的要求不大,当设置好后有相当大的可移植性和通用性.

[1] 张国良.模糊控制及其MATLAB应用[M].西安:西安交通大学出版社,2002.

[2] 王立新.模糊系统与模糊控制教程[M].北京:清华大学出版社,2005.

[3] 陶永华.新型PID控制及其应用[M].北京:机械工业出版社,2003.

[4] 诸静.模糊控制原理及应用[M].北京:机械工业出版社,1999.

[5] 李秀娟,于力.基于MATLAB模糊控制器设计和仿真[J].电子测量技术,2004(3):22-23.

[6] 齐琳.模糊PID动态切换控制算法的研究[D].北京:北京交通大学,2007.

[7] Takagi T,Sugeno M.Fuzzy Identification of Systems and Its Applications to Modeling and Control[J].IEEE Transactions on SMC,1985,15(1):116-132.

[8] 吴进华,吴华丽,陈世童,等.基于MATLAB的调整系统控制量的模糊 PID控制器的实现[J].海军航空工程学院学报,2009,24(2):175-177.

[9] Chen G.Conventional and Fuzzy PID Controllers:An Overview[J].Int J of Intelligent Control Systems,1996(1):235-246.

[10] 郑浩鑫,郑宾,殷云华.模糊PID数字控制器系统的仿真与设计[J].机械工程与自动化,2009(2):121-123.

[11] 毛义梅.一种PID参数模糊自整定控制器的设计与仿真[J].自动化与仪表,2001,16(3):37-38.

Performance Simulation Analysis of Fuzzy PID Control

LI Jian-chun,LI Xiang-bai
(Yunnan Chihong Zn&Ge Co.,Ltd.,Qujing 655000,China)

Fuzzy PID control with the advantages of classic PID and Fuzzy control,has very good control performance.By summarizing currently popular control methods,the paper studies various control structures.Simulation analysis with the Fuzzy module of Simulink in Matlab,comparing with their respective advantages and disadvantages,draws conclusions for the design of Fuzzy PID control system.

Fuzzy control;PID;simulation

TP273.4

A

10.3969/j.issn.1671-6906.2010.06.014

1671-6906(2010)06-0059-05

2010-11-08

李建春(1982-),女,山西朔州人,硕士.