模糊数学在市场比较法中的应用分析

杨 振

(大连大学经济管理学院,辽宁大连 116622)

模糊数学在市场比较法中的应用分析

杨 振

(大连大学经济管理学院,辽宁大连 116622)

运用模糊模式识别模型进行可比实例的选择,运用模糊综合评判模型进行区域因素和个别因素的确定,平滑指数法求取待估房地产综合价格,最后,进行实例研究,证明改进后的方法的可行性。市场比较法的改进减少因评估人员主观性造成的精确度不高的问题,提高评估的价格精度。

市场比较法;模糊模式识别;模糊综合评判;平滑指数法

1 引言

市场比较法是将估价对象与在估价时点近期交易的类似房地产进行比较,对这些类似房地产的成交价格做适当的修正和调整,以此求取估价对象的客观合理价格或价值的方法[1]。运用市场比较法估价时,有不少特征因素在概念上没有明确的外延或难以量化,不能用精确的数值来衡量,因此,估价结果带有一定的主观性。而模糊数学正是研究现实世界中许多界限不分明甚至很模糊的问题的数学工具。为改善市场比较法中由于估价人员主观性造成的偏差,本文将模糊数学理论引入房地产估价市场比较法中进行研究。

2 模糊数学理论的相关概念

2.1 隶属度

定义 论域E上的模糊集合A由隶属函数μA(x)表征,其中x∈E,μA(x)在区间[0,1]上取值代表x对A的“隶属程度”,简称为隶属度[2]。

隶属度是表示某些元素隶属于某种特征的函数,用介于0和1之间的实数来表示隶属程度,其值越接近1,隶属程度越高。为了使得房地产评估师给出的隶属度更为精确,可更细致的划分区间赋值的范围:极相似为(0.8,1),相似为(0.6,0.8),一般相似为(0.4,0.6),不相似为(0.2,0.4),极不相似为(0,0.2)。

2.2 择近原则

设论域为U,A1、A2、ΛAn是论域U上的n个模糊集合,其构成一个标准的模型库。B∈ Γ(U)为待识别的模型。若存在i=1,2,Λn,使得σ(A1,B)=m ax[σ(A1,B),σ(A2,B), Λ σ(An,B)],则认为B与Ai最贴近[3]。

隶属度是用于识别单个确定的元素,择近原则用于识别群体模型。在运用市场比较法选择可比实例时,需要识别的对象不是单个确定的元素,而是论域上的模糊子集,因此,在识别房地产可比实例时,应用择近原则更为合适。

3 市场比较法评估模型构建

3.1 模糊模式识别模型选取可比实例

设已知有n个已成交的房地产实例A1、A2、ΛAn、,用Ti表示i个已估房地产的特征向量。则Ti=(tn1,ti2,Λ,tim),式中m表示特征向量的个数,tij表示已成交的房地产特征因素的隶属值。在选择可比实例时,须保证可比实例与待估价房地产的用途和结构相同,时间相近,且处于同一供求圈。所以影响待估房地产与已估房地产价格差异的主要因素是区域因素和个别因素。找出两者的差异程度,即可得出两者的隶属度。下面应用模糊综合评判法计算区域因素和个别因素的隶属度。

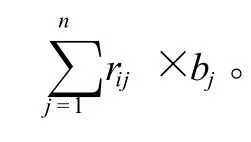
将矩阵F和F′各元素除以10,即为隶属度Ti和Ti′。代入贴近度公式,即可算出待估房地产Ti′与已估房地产Ti的贴近度α1,α2,Λ αn,按从大到小的顺序排列,记为σ1,σ2,Λ σn,相应的修正后的房地产价格为P1,P2,ΛPn。一般情况下αiσi,。根据择近原则,第一个可比实例与待估房地产最为相似,第二个次之,第三个再次之,依次类推,第n个最不相似。当贴近度相同时,可利用模糊关系系数的大小来排序[4]:

3.2 房地产状况的调整

3.2.1 .交易日期调整

其中,S为交易日期修正系数;

SP

＊为评估时点的价格指数;

SP为可比实例交易日期的房地产价格指数

3.2.2 .区域因素修正采用模糊综合评判法进行区域因素修正。区域因素集U={x1,x2,Λ,xn}(xi分别代表区位、繁华程度、交通便捷度及环境景观等)。V=(v1,v2,Λ,v5)=(优,较优,一般,较劣,劣) ={10,8,6,4,2};区域因素各因子用途不同,权重也不同。请房地产评估师对交易实例和待估对象的各因素进行评判打分,待估房地产的区域因素的单因素评判矩阵[5]为:

3.2.3 .个别因素修正

个别因素修正与区域因素修正方法一样,也采用模糊综合评判法。个别因素集U′= {x′1,x′2,Λ,x′n}(x′i分别代表建筑物情况、临街情况、设施状况及装修状况等);采用五级评分法建立评判标准集V=(v1,v2,Λ,v5)=(优、较优、一般、较劣、劣)={10,8,6,4,2},个别因素各因子的权重:A′=(a′1,a′2,Λ,a′n)。

由此可求出个别因素修正系数为:

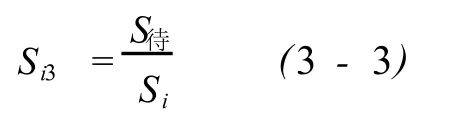
则修正后的交易实例价格为:

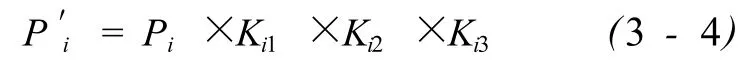
3.3 指数平滑法建立模糊数学评估模型

在房地产评估中,可通过指数平滑法建立模糊数学评估模型,求取待估房地产的综合价格。在指数平滑法中,将可比实例的价格乘以相应贴近度的权重来调整选择可比实例,从而得出可比实例的比准价格。相似度越高的可比实例,权重越大,所起的调节作用就越大;反之越小。

设第i个可比实例价格的评估值为S＊i,相应的可比实例的比准价格为Si,其评估误差为Si-S＊i,则第i-1个可比实例价格的评估值为(按照指数平滑法建立评估模型[38]):

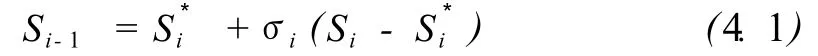
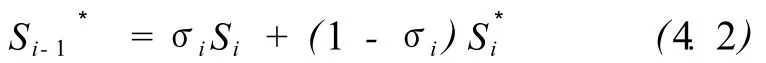
按上式依次类推并展开,则可得到待估房地产的评评估格为

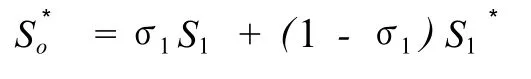
从上式可知,评估对象的评评估格即为各可比实例价格的加权平均值,这些权值从大到小地变化,逐渐趋于零,且权值之和等于1,即

上式即为模糊数学评估模型,据此可求得待估房地产更精确的评估价格。

4 实例研究

结合上述理论,现用模糊数学评估模型对大连名仕财富大厦房地产评估项目价值进行分析估算。

大连名仕财富大厦坐落于大连市中山区港湾街,东邻勤俭街,南望二七广场,西邻五五路,北接港湾广场,地处中山区核心地带,周边基础配套设施完善,公共交通便捷。该栋大厦主要用于商务办公,周围类似商务大厦较多,买卖和租赁市场活跃,可比实例较多且易于获得,非常合适用市场比较法进行评估。

4.1 建立评价指标体系

根据该大厦的特点,首先建立该楼的评价指标体系。影响商务楼宇价值的因素主要包括两部分:区域因素和个别因素。区域因素中,影响商务楼宇最大的因素是区位因素,即所处位置和周围商业等级。个别因素中,影响楼宇价值最大的因素是建筑物情况,即建筑物建筑年代、建筑结构、装修程度等。

共有10位房地产评估师参与该项目评价(见表1)。在表中,第一行“坐落位置C111”对应的(0.6,0.4,0,0)表示对待估对象在"坐落位置"因素方面有6位房地产评估师认为是优,4位房地产评估师认为较优,其余因素类似。

这里S(Q)S(Q),S(Bij),S(ijk),均为评估论域:U={优,较优,一般,较劣,劣}={u1, u2,u3,u4,u5}上的模糊集合。

最后把S(Cijk)的每一个评估结果与一个分值对应起来(见表2),利用相应分值可以将评估结果化为一个确切的分值F。

表1 因素指标评估表

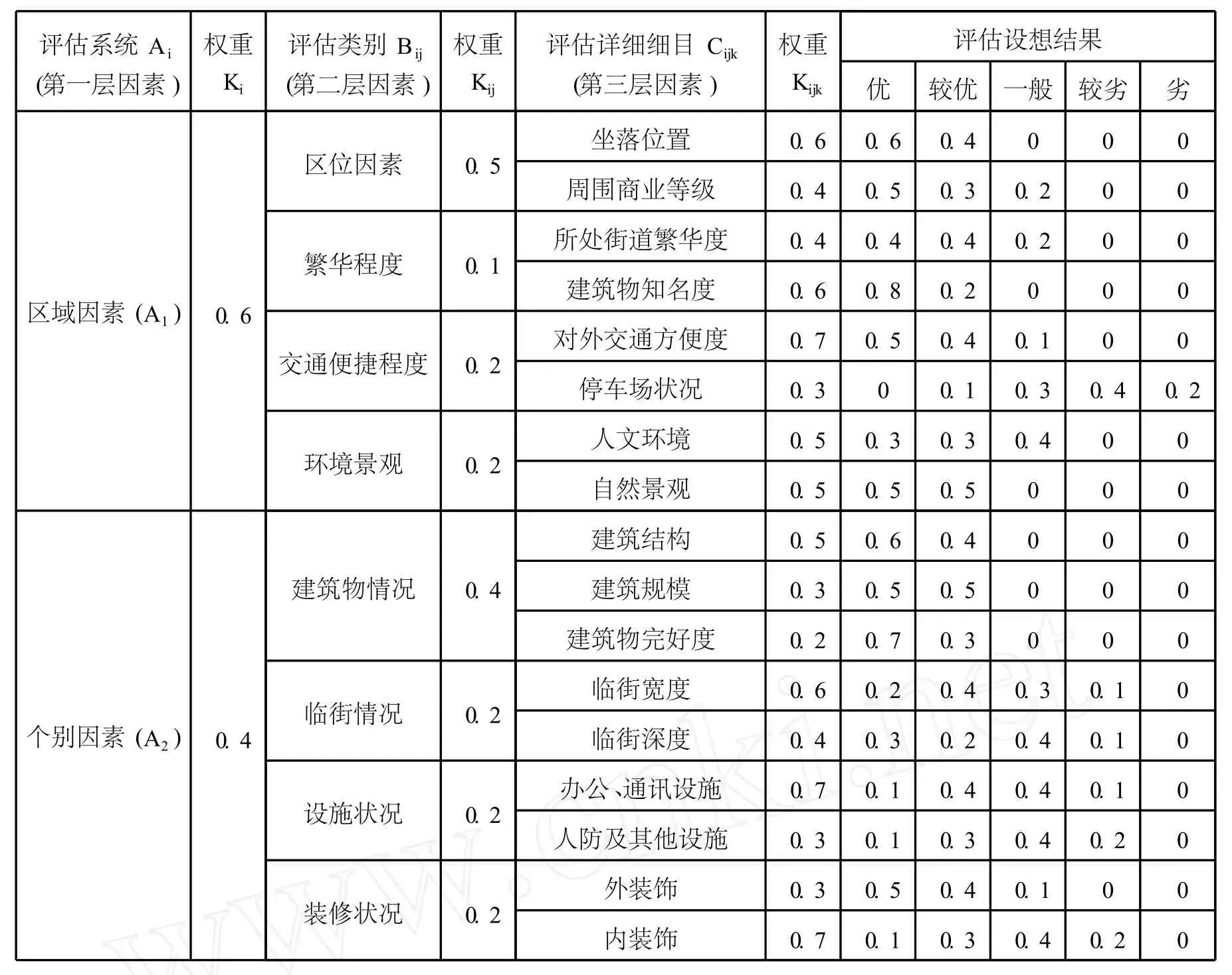
表2 评估结果对照表

同理,将可比实例进行相同计算并得出相应分值,然后根据直线内插法得出待估房地产的价格。

4.2 区域因素的综合评估计算

4.2.1 区域因素中“区位因素B11”的综合评估计算:

4.2.2 区域因素中"繁华程度B12"的综合评估计算:

4.2.3 区域因素中"交通便捷度B13"的综合评估计算:

4.2.4 区域因素中"环境景观B14"的综合评估计算:

因此,10位房地产评估师对名仕财富大厦的区域因素的综合评估结果为:50.4%为很好,34%为好, 12%为一般,2.4%为不好,1.2%为很不好。

4.3 个别因素的综合评估计算

个别因素的综合评估计算与区域因素的综合评估计算一样,由于篇幅所限,本文不再赘述详细的计算过程,仅给出计算结果。

(1)个别因素中"建筑物情况B21"的综合评估计算:

则有S(A2)=(0.348,0.368,0.21,0.074,0)。因此,10位房地产评估师对名仕财富大厦的个别因素的综合评估结果为:34.8%为优,36.8%为较优,21%为一般,7.4%为较差,其余为零。

4.4 因素指标评估表初次综合计算

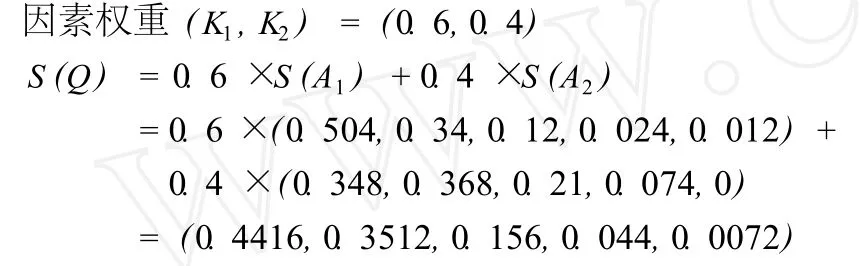
4.5 综合评估结果计算

上述综合评估结果表明,对名仕财富大厦的总体评估结果为:44.16%为很好,35.12%为好,15.6%为一般,4.4%为不好,0.72%为很不好。

即名仕财富大厦综合评估结果为81.76分。

4.6 待估房地产价格计算

同理对可比实例A、B、C进行价值因素指标评估(计算过程略,方法同上)得出相应的最后分值为:FA= 80.13分;FB=80.96分;FC=80.94分。

由以上计算可得表3:

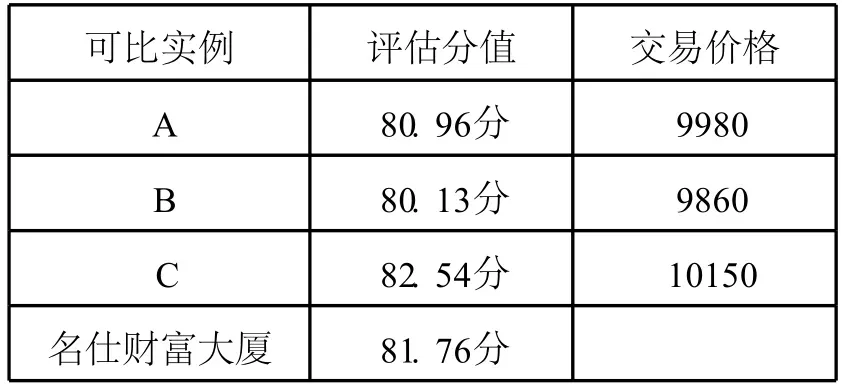
表3 可比实例评估分值及交易价格表

最后根据直线内插法计算,待估对象的价格为:

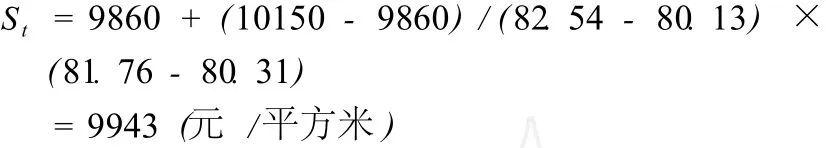
5 结论

将模糊数学理论引入市场比较法,用模糊模式识别模型进行可比实例的选择,用模糊综合评判模型进行区域因素和个别因素的确定,用平滑指数法进行综合价格的求取,进而建立房地产估价市场比较法的估价模型,可以消除因估价人员的主观性造成估价结果的偏差,对房地产评估市场比较法的改进具有重要的理论价值和实践指导意义。

[1]施建刚.房地产估价方法的拓展[M],上海:同济大学出版社,2003,12-13

[2]谢季坚,刘承平.模糊数学方法及其应用[M],武汉:华中理工大学出版社,2005,124-125

[3]薛景歧.宗地地价的模糊综合评价[M],辽宁:辽宁大学出版社,2004,52-54

[4]张宗元.模糊数学入门和在建筑管理中的应用[M].北京:中国建筑工业出版社,2006

[5]赵耀文.地产估价中的模糊数学模型.数量经济技术经济研究[J],2007(3),59-61

Application Analysis on the Market Comparison Approach Based on FuzzyMath

YANG Zhen

(College of Economics andManagement,Dalian University,116622,China)

This papermakes an alternative for the comparable cases by using the fuzzy recognition mode,defines the regional and individuals factor based on the fuzzy evaluation model,gets comprehensive prices by using the smoothing index and then analyzes a case to test the feasibility of improved method.This paper explains the improved method of market comparison is benefit to reduce the low accuracy caused by the subjective assess ment of staff and rise the evaluate price accuracy aswell.

market comparison approach;fuzzy recognition pattern;fuzzy comprehensive evaluation;s moothing index

C962

A

1008-2395(2010)06-0015-05

2010-04-29

杨振(1984-),男,大连大学经济管理学院硕士生。