关于模糊C-均值(FCM)聚类算法的改进
王颖洁,白凤波,王金慧
(1.大连大学信息工程学院,辽宁大连 116622;2.北京海辉高科软件有限公司微软事业部,北京 100085; 3.北京机电工程研究所,北京 100074)
关于模糊C-均值(FCM)聚类算法的改进
王颖洁1,白凤波2,王金慧3
(1.大连大学信息工程学院,辽宁大连 116622;2.北京海辉高科软件有限公司微软事业部,北京 100085; 3.北京机电工程研究所,北京 100074)
对模糊C-均值聚类算法的改进,即在原有的模糊C-均值算法的基础上,用一种新的定义距离的方法替代欧氏空间中距离的定义,改进模糊聚类算法。并且用数据仿真验证这种改进的模糊聚类算法与原来算法相比,聚类效果更好,分类更清晰。
模糊C-均值算法,模糊加权距离,模糊加权因子
1 引言
模糊聚类分析(FCA)的思想首先是由Bel lman和Zadeh等人在1966年提出的,它是近些年来发展很快的一种分析方法,其目的是对样本进行合理分配,从而达到对样本进行判别、分析与预测的目的。1973年Dunn提出了模糊C-均值聚类法(FCM);1992年Bezdek提出一种"Fuzzy Kohonen Clustering Network"算法(FKCN),Bezdek的FKCN算法是将神经网络用于求类中心的迭代问题,该算法中没有考虑模式特征的重要性描述,因此迭代速度慢。目前有关模糊聚类的许多成果都是对C-均值聚类法进行推广和改进。该文讨论的是对模糊C -均值聚类算法的改进,这种改进算法的核心部分是引进了一种新的定义距离的方法-模糊加权距离。
2 FCM算法
模糊C-均值聚类问题在数学上可以表示为如下的目标函数[1]求极值的问题:
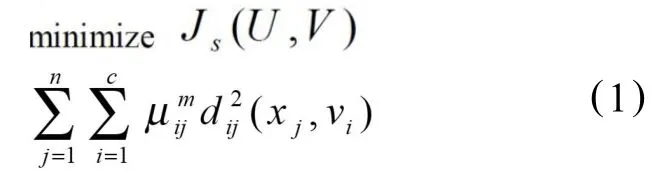
约束条件为:
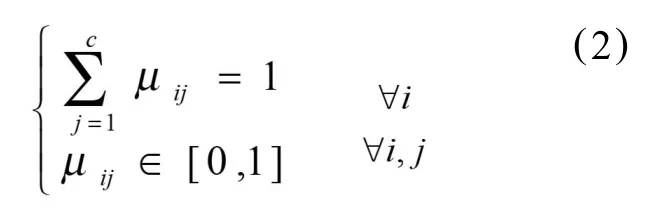
式中n为样本数据点的数目,c为类别数目,通常1<c<n;m>1为一个标量;dij(xj, vi)=‖xj-vi‖示数据点xj心之间的欧氏距离;X={x1,x1,Λ,xn}⊂Rs点的集合,vi∈Rs为聚类的中心;μij表示数据点xj属于类中心vi的隶属度。U={μij}是一个n×c的模糊分割矩阵,V={v1,v2,Λ,vc}是一个s×c的矩阵。
m用来控制分割矩阵U的模糊程度,m越大,分类的模糊程度越高,m→∞时,μ=→1/c,实际上已不能提供分类信息;当m=1时,μij∈[0,1],算法退化为HCM算法,所以FCM实质上是HCM的自然推广。欧氏距离准则适合于类内数据点为超球型分布的情况,dij采用不同的距离定义,可将聚类算法用于不同分布类型数据的聚类问题。
3 改进的模糊聚类算法
3.1 引入加权因子的模糊加权距离
距离是模式识别与分类、聚类分析及现实社会中非常重要的概念之一,它反映了事物之间的近似程度。模糊加权距离[2]是一种新的定义距离的方法。模糊加权距离的加权因子是根据数据空间中各数据点对同一聚类中心的贡献(即所起的作用)不同而确定的。
(1)先对模糊子集和隶属函数进行定义。
设给定论域为U,U上的一个模糊子集A是指:对任X∈U,都确定了一个数μA(x)且μA(x)∈[0,1],称μA(x)为x对A的隶属程度.
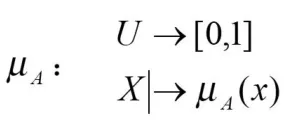
μ称为模糊子集A的隶属函数,模糊子集完全由其隶属函数所刻画。
(2)提出一个新的概念-模糊加权因子。模糊加权因子的性质类似于隶属度,但作用不同于FCM算法中的隶属度μij,它与隶属度分别侧重于两个不同的方面。每一个数据点xj相对于每一个聚类中心center(i)都有一个隶属度μij(μij是初始化的隶属度矩阵中第i行j列位置上的元素并且Σci=1μij=1),所以同一个数据点对于不同的聚类中心可以用隶属度来表示其优势程度。但对于同一个聚类中心来说,不同的数据点之间的隶属度就没有任何的联系,也就是说每个数据点对同一个聚类中心来说对于距离的贡献是无法比较的。举个简单的例子:
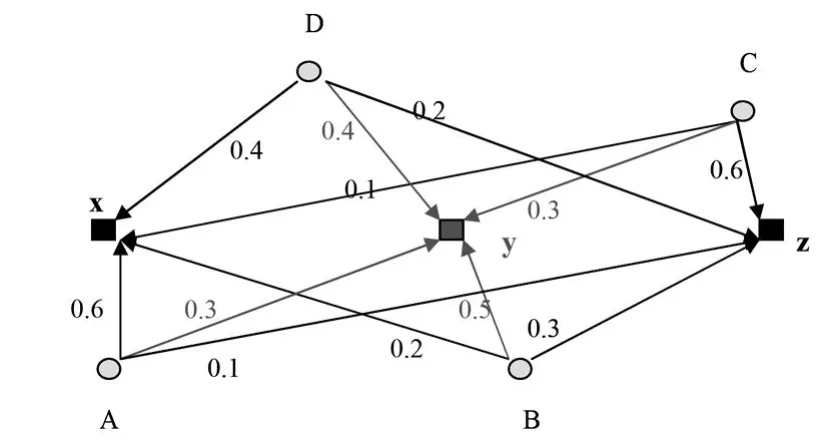
图1 举例说明模糊加权因子
如图1:A,B,C,D是四个数据点,x,y,z是三个聚类中心。数据点A对于三个聚类中心x, y,z的隶属度分别是0.6,0.3,0.1,三者之间可以比较,数据点A属于聚类中心x的可能性更大一点。但对于同一个聚类中心x来说,四个数据点A,B,C,D原来的隶属度已没有可比性,对于距离没有任何意义。所以提出一个模糊加权因子的概念。
(3)加权因子的确定[3-5]。定量给出了每个数据点xj隶属于同一个聚类中心center(i)时所具有的优势程度。模糊加权因子,描述各个数据点对距离的贡献是不平等的(距离是聚类中心center(i)到数据点xj的距离)。
其定义如下:
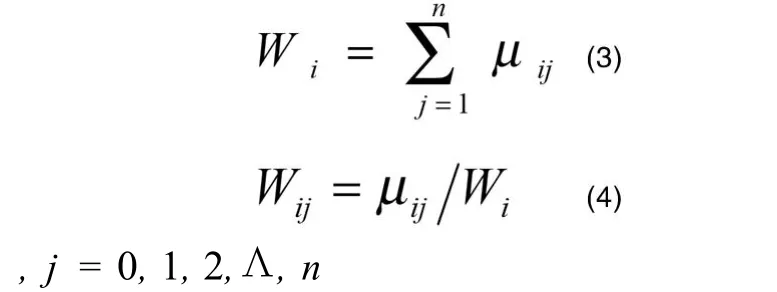
Wij即为是第j个数据点属于第i个聚类中心的模糊加权因子。在这里,μij是第j个数据点属于第i个聚类中心的隶属度,n是数据点的个数。
(4)模糊加权距离的定义
在模式识别与分类中,常常只求距离的平方而不必求出距离本身,这仅仅是为避免开方运算(欧式空间中),并不影响讨论结果,因此这里亦以平方形式给出加权距离的定义:
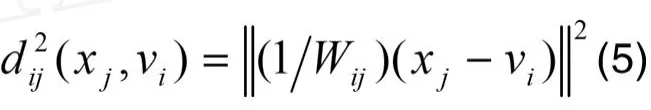
其中Wij由式(4)确定。可以证明式(5)满足距离空间中关于距离的定义。
下面我们讨论1/Wij的意义。当Wij越大,则表示在各数据点到聚类中center(i)的距离中, xj所起的作用越大,即对距离的贡献越大。xj对距离的贡献越大就表示它距离聚类中心center(i)越近,1/Wij越小,距离放大的尺度就越小,所以距离值越小。举个例子:(参见图1)假定A,B,C,D四个数据点到聚类中心z的欧式距离分别是10,4,2,8。利用(3)和(4)式可以求出WZA=1/12;WZB=1/4;WZC=1/2;WZD= 1/6。将上述代入到(5)式中得到模糊加权距离dZA=120;dZB=16;dZC=4;dZD=48。
模糊加权距离的原理就是将模糊加权因子引入到欧氏空间距离公式中,模糊加权因子的倒数就相当于一个放大镜的作用,将所有的距离全部放大,但是放大的尺度不同,对于距离远的数据点放大的尺度要大一些,对于距离近的数据点放大的尺度要小一些。这样就导致了两极分化,距离远的变得更远,距离近的变得更近,使得更易于聚类,分类清晰,得到很好的聚类效果。
3.2 改进的模糊聚类算法
下面将模糊加权距离引入到模糊C-均值聚类算法中,模糊C-均值聚类算法中的其他的定义没有变化,只有求极值的目标函数中距

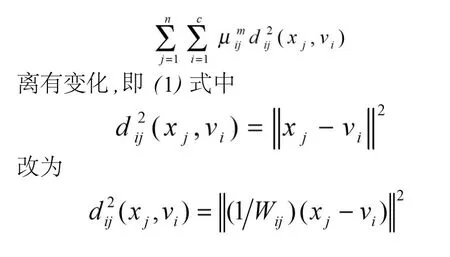
其中Wij为模糊加权因子,由式(5)确定。
在模糊C-均值算法中引入模糊加权因子,使得数据空间中各个数据点对同一聚类中心所具有的特征优势不同,导致对距离的贡献也不同,更具合理性,使得聚类效果更好,分类更清晰,改进数据预处理的方法。
4 数据仿真结果
将200个二维数据分为三类。使用了两种方法,本文提出的改进的模糊聚类算法(引入了模糊加权因子),结果见图2;经典的模糊C-均值聚类算法[6],结果见图3。对比聚类效果图如下:
通过对比两种算法的效果图可以看出:图2是改进后的模糊聚类算法(引入了模糊加权因子)的效果图,聚类效果比图3经典的模糊C -均值聚类算法更好,数据点更集中,有若干点集中在聚类中心上。我们可以看右下角的数据点,改进后的模糊聚类算法将紫色的点和蓝色的点能清楚的分开,两个类之间的界限很明显;而模糊C-均值算法分类的程度就不是很清晰,分别属于两个类的绿色的点和紫色的点几乎重合,可见类与类之间划分不清晰。
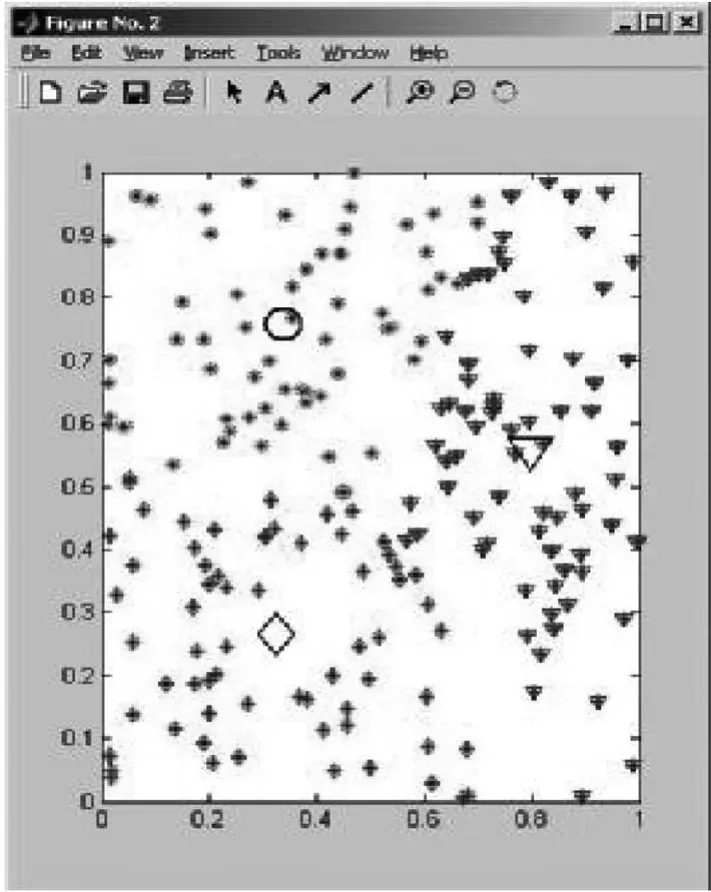
图2 改进算法后的聚类效果图

图3 FCM聚类效果图
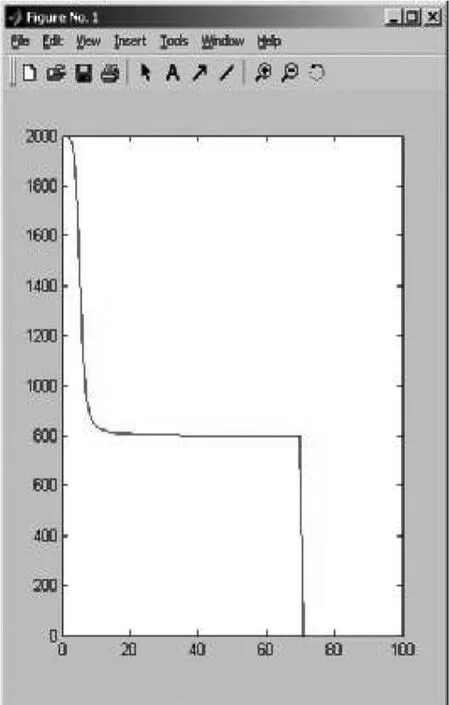
图4 改进算法后的目标函数图

图5 FCM目标函数图
对比目标函数曲线如下:图4的是改进算法后的目标函数图(引入模糊加权因子),图5是经典的模糊C-均值算法目标函数图。可以看出图4的函数曲线比图5的函数曲线更加平滑,收敛速度快。
5 结论
本文讨论的是对模糊C-均值聚类算法的改进,在原有的模糊C-均值算法的基础上,用一种新的定义距离的方法替代欧氏空间中距离的定义,引入了重要参数-模糊加权因子,模糊加权因子的引入,使得数据空间中各数据点所具有的特征优势不同,导致对距离的贡献也不同,这是两种距离定义方法的根本区别之处。并且用数据仿真验证了这种改进了的模糊聚类算法比原来的算法聚类更有效,分类更清晰,速度快。
[1]Timothy J.Ross.模糊逻辑及其工程应用[M].北京:电子工业出版社,2003.
[2]鲁宇,范希鲁.模糊加权距离及其合理性讨论[J].北方交通大学学报,1990(2).
[3]王士同.神经模糊系统及其应用[M].北京:北京航天航空大学出版社,1998(6).
[4]Kazutaka Umayahara,Sadaaki MiyamotoandYoshiteru Nakamori,Formulations of Fuzzy Clustering for Categorical Data,InternationalJournalofInnovativeComputing, Information and Control(IJICIC),vol.1,no.1,pp.83-94,2005(3).
[5]Hugang Han,InformationSystem withFuzzy Weights, International Journal of Innovative Computing,Information and Control(IJICIC),vol.2,no.3,pp.553-565,2006 (6).
[6]吴晓莉,林哲辉.MATLAB辅助模糊系统设计[M].西安:西安电子科技大学出版社,2002.
Improvement of the Fuzzy C-Means Clustering Algorithm
WANG Ying-jieWang1,BA IFeng-bo2,WANG Jin-hui3
(1.College of Infor mation Engineering,Dalian University,Dalian,116622,China;
2.MSPD,HiSoft Technology InternationalLtd.,Beijing,100074,China;
3.Beijing Electromechanical Engineering Insitute,Beijing,100074,China)
An improvement algorithm about the fuzzy c-means clustering algorithm is discussed in this paper.Based on original fuzzy c-means clustering algorithm,the improvement algorithm uses a new way of defining distance to displace the distance in Euclidean space.Experimental results show that the improvement algorithm is better than original algorithm and the classification is clearer than original algorithm.
Fuzzy c-means algorithm;Fuzzyweighted distance;Fuzzyweighted factor
TP18
A
1008-2395(2010)06-0001-04
2010-11-15
王颖洁(1977-),女,讲师,Email:yingjiehappy@hotmail.com

