一维浅水波方程有限体积流通量限制方法的数值研究

刘红霞 赵彦普

(1.东莞职业技术学院，广东东莞 523808)

（2.中国科学院深圳先进技术研究院，深圳 518055)

浅水波方程是水动力学中一个重要模型，在地球大气、海洋、环境及水利工程、清洁能源的开发利用等领域有广泛应用.由于该模型是非线性守恒方程组，其解的结构比较复杂，需借助于数值模拟的方法进行求解.本文要讨论的1维齐次浅水波模型方程为：

其中h代表水流高度，u代表水流速度，g代表重力加速度.上述方程组中第一个方程表示质量守恒，第二个方程表示动量守恒.

有限体积法又称为控制体积法.由该方法得到的离散方程，就是状态变量在控制体积中的守恒原理.有限体积方法构造守恒数值格式，在求解守恒方程方面有先天的优势.本文将针对几种简单实用的数值流通量以及几种常用的流通量限制器之间的组合搭配进行讨论，以期得到针对一维浅水波方程组的更精确的数值求解计算方法.

1 有限体积方法以及算法实现

1.1 有限体积方法

设我们要求解的标量或者向量双曲守恒方程为：

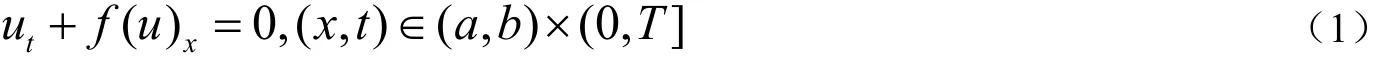
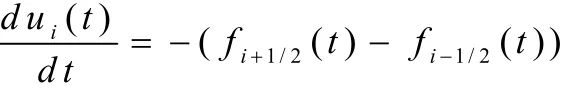
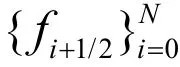
1.2 数值流通量

有限体积方法的格式设计紧密依赖于数值流通量 fi+1/2(t)的选取，对于一维浅水波方程组，将用到以下几种数值流通量：

1）Lax-Fridrichs（LF）数值流通量

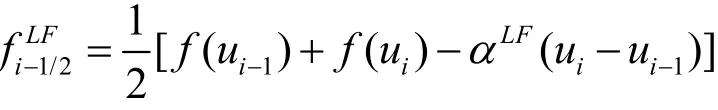
2）Roe数值流通量

3）HLLE数值流通量

4）FORCE数值流通量

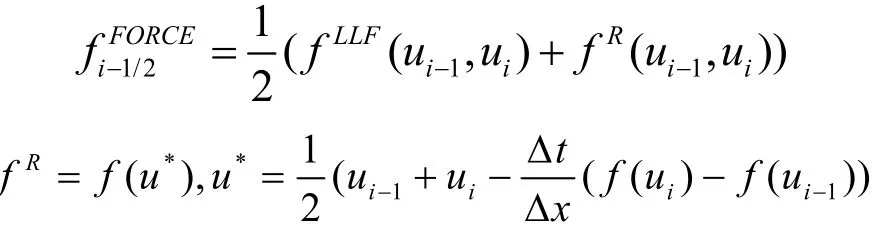
5）基于Lax-Wendroff格式和Roe线性化的数值流通量

1.3 数值算法

本文采用的数值流通量的一般形式为：

流通量限制器函数φ()θ定义为：

2 数值算例

2.1 一维溃坝问题

我们选取三种不同的浅水波方程（见表 1）来检验本文方法的效果.以下重力加速度选取为g= 1，空间区域取为(-5,5)，边界条件为Dirichlet边界.

表1 三种不同的浅水波方程

2.2 模拟结果

以下计算结果均为计算到终止时间 t=1，均匀空间网格，单元数量为100.

图1 问题I，固定数值流通量，不同流通量限制器函数下的计算结果

从图1可以看出，对于问题I，在固定LF流通量，选取不同的限制器函数时，选取的流通量限制方法均能达到较好的抑制大梯度区域的非物理振荡的效果.从局部放大效果来看，除Minmod限制器函数之外的三个限制器函数更能保持解在激波附近的大梯度变化.

图2 问题I，固定流通量限制器函数，选取不同数值流通量的计算结果

从图2可以看出，对于问题I，在固定van Leer限制器，FORCE数值流通量计算结果在 2-激波的间断附近出现了些许振荡，其余几个流通量函数表现相当且没有出现激波位置的振荡，这说明FORCE数值耗散在5个流通量中最弱，但同时FORCE数值最能保持解在间断附近的陡峭变化.LF数值流通量是这5个数值流通量中数值耗散作用最强的.

图3 问题II，固定数值流通量，选取不同流通量限制器函数的计算结果

从图3可以看出，对于问题II，在固定Roe流通量，选取不同的限制器函数时，所选取的方法均能达到抑制大梯度区域的非物理振荡的效果；MC限制器函数最能保持解的大梯度变化；Superbee限制器下的数值解在x=-1附近出现了小的振荡.

图4 问题II，固定流通量限制器函数，选取不同数值流通量的计算结果

从图4可以看出，对于问题II，在固定van Leer限制器，选取不同的数值流通量时：FORCE数值流通量计算结果在 2-激波的间断附近出现了微小振荡，其余几个流通量函数表现相近且没有出现激波位置的振荡；对于不同的限制器函数，HLLE数值流通量计算结果比较精确.

图5 问题III，固定数值流通量，选取不同流通量限制器函数的计算结果

从图 5可以看出，对于问题 III，在固定 Roe流通量，选取不同的限制器函数时，此方法均能达到较好的抑制大梯度区域的非物理振荡的效果；从局部放大效果来看，Superbee限制器函数更能保持解的锐利图形.

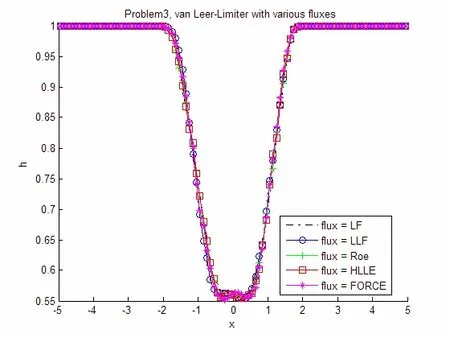
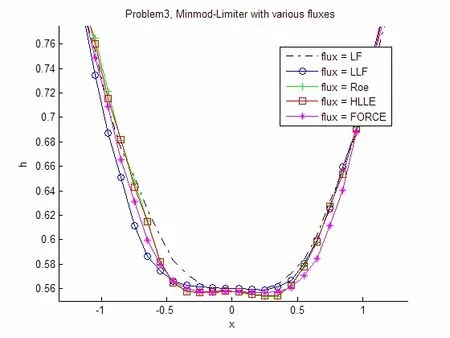
图6 问题III，固定流通量限制器函数，选取不同数值流通量的计算结果

从图6可以看出，对于问题III，在固定van Leer限制器，选取不同的数值流通量时，均能得到较精确的计算结果.其中FORCE数值流通量在1-稀疏波与 2-稀疏波之间的常值区域出现了一些小的波动，其余几个流通量函数结果相近.另外对于该初值问题，对于不同的限制器函数，LLF数值流通量表现比较准确.

3 结 论

本文采用基于流通量限制器的有限体积方法，通过限制器函数使低阶数值流通量与高阶数值流通量得到有效结合.并且通过3个特殊的浅水波方程初值问题，对该方法的效果进行了数值比较.比较结果显示该方法能较好地计算出激波，稀疏波的结构；对于不同初值，不同的限制器与不同的数值流通量有不同的表现；LLF流通量和Superbee的组合是数值耗散最弱的同时也能有效抑制非物理振荡.

[1]汪继文，刘儒勋.间断解问题的有限体积法[J].计算物理，2001，18（2）:97-105.

[2]韩涛，逢勇，翟金波.基于间断有限元求解浅水方程[J].西安交通大学学报，2007（3）:377-379.