界面对颗粒增强金属基复合材料强化性能的影响
张 鹏,李付国
(西北工业大学材料科学与工程学院,西安710072,E-mail:fuguolx@nwpu.edu.cn)
界面对颗粒增强金属基复合材料强化性能的影响
张 鹏,李付国
(西北工业大学材料科学与工程学院,西安710072,E-mail:fuguolx@nwpu.edu.cn)
为提高颗粒增强金属基复合材料的力学性能,采用基于微观组织的胞元模型建模方法,并利用有限元软件ABAQUS着重分析了界面层厚度以及界面层强度对复合材料性能的影响,通过对复合材料中各组成部分的应力、应变云图的获取,形象地说明了各部分的变形规律.研究结果表明,在弱界面层下,随着界面层厚度的增加,复合材料的强化效果并不显著,而在强界面层下,随着界面层厚度的增加,强化效果非常明显;就界面层强度来说,界面越强,所表现出的强化效果就越明显,但当界面层强度比基体大得多时,随着界面层强度的增加,虽然复合材料的强化呈递增趋势,但是递增的幅度已逐渐降低.
颗粒增强金属基复合材料;界面层;强化;胞元模型
颗粒增强金属基复合材料由于具有高的比强度、比刚度及良好的耐磨性、热稳定性等优点,已被众多材料科研工作者所广泛关注[1-2].增强相的加入提高了复合材料的力学性能,但增强相对复合材料力学性能的影响是复杂的,比如增强颗粒的大小、分布、形状,以及界面等因素.到目前为止,增强相的大小、分布和形状对复合材料力学性能的影响已经进行了深入的研究,并取得了一定的成果,增强颗粒越小,越有利于复合材料性能的提高,材料越不容易失效[3-5];颗粒越圆滑,少尖角,则不易使材料产生应力集中而导致界面位置破裂[6];颗粒分布越均匀,材料变形过程中所承载的应力或应变场分布就越均匀,从而就不易产生局部应力集中现象[7-10].但是界面作为影响复合材料性能的一个重要因素,目前的研究结果相对较少,陈尚平等[11]在研究中指出,基体与增强颗粒之间的界面结合力是铝基复合材料性能的控制因素,也是决定复合材料强化效果的根本因素;而郭成等[12]研究发现复合材料的强化效果取决于基体强度与界面强度的匹配关系,并非完全由界面结合力来控制.由此可以看出界面层对复合材料强化效果的本质影响机理并未达成共识,因此界面对于复合材料性能的影响有必要做进一步的研究.
通常在复合材料的制备过程中,界面的形成受多种因素控制,如温度、时间、SiC表面的氧化程度以及基体中加入的合金元素等,如果SiC表面具有SiO2层,其反应厚度符合S=At1/2的规律[13],其中S为界面层厚度,t为时间,A为系数;如果复合材料采用铸造法制备,SiC颗粒在搅拌分散的过程中,当混合体的温度升至550℃保温搅拌时,可能发生界面反应,并且温度越高,停留时间越长,反应越激烈,反应程度也越大[14].因此在制备方法与工艺参数的选择上,首先需要考虑制备温度以及高温下停留的时间,确保制备出的复合材料具有较高的强度.
本文采用数值模拟的方法,建立了基于实际微观组织的胞元模型,并在模型中加入界面层,通过改变界面层参数的方法来研究界面对复合材料性能的影响.
1 试验
试验材料为粉末冶金法制备的SiC颗粒增强铝基复合材料,其中 SiC颗粒的体积分数为15%,在制备过程中,首先把烘烤干燥的SiC粉末与铝合金粉末机械混合,然后把粉末混合物进行高能球磨,制备成复合粉末,随后用包套真空热压工艺把复合粉末冷等静压成坯锭,并装入铝包套,加热、抽真空、封死.再把带有包套的坯锭热压成形.为了研究所制备的复合材料界面特性对复合材料性能的影响,所选用的金相样本如图1所示.

图1 复合材料微观组织
2 有限元模型
2.1 胞元模型
本文建立的模型分为两类:有界面层和无界面层.根据图1所建的这两类胞元模型如图2(a)和图2(b)所示.建立模型时,首先按照标尺把图像还原回原始尺寸,还原后的尺寸为135 μm× 110 μm,然后按照实际尺寸建立胞元模型.对比金相图片与胞元模型可知,所建立的模型与实际微观组织中增强颗粒大小、形状、位置、以及分布非常相似,但一些颗粒位于图像的边缘,所以在施加界面层的时候,会导致界面超出模型的边界,因此在建立模型时,把图中一些位于边缘和非常小的颗粒省略掉了.本文在分析中,界面层的厚度分别取1、2、2.5 μm.对于一些相距比较近的颗粒,当颗粒的界面层厚度增加时,就容易使几个颗粒的界面层连为一体,如图2(c)所示.当界面层厚度为2.5 μm时,就会出现这种现象.
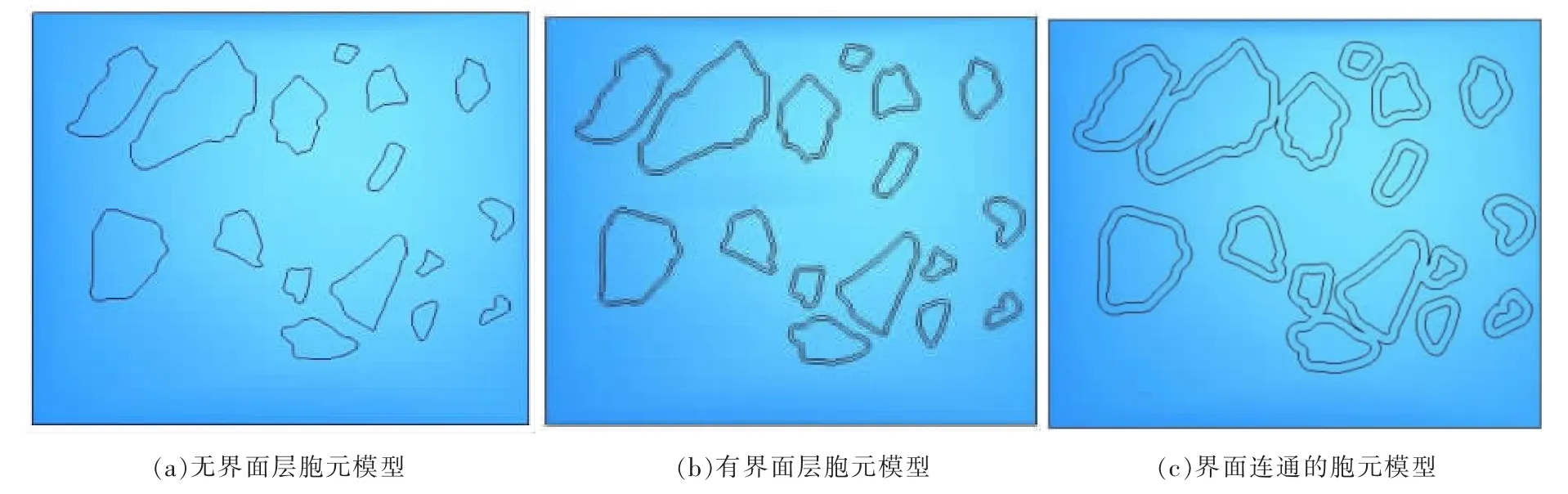
图2 胞元模型
2.2 材料参数
基体铝合金视为各向同性的弹塑性材料,并服从Von Mises准则,其流动应力模型[15]满足关系式

式中:σY为流动应力;σ0Y为初始屈服应力;h为硬化系数;为等效塑性应变;n为硬化指数.
增强颗粒SiC视为弹性体材料.如果有下标1代表基体,有下标2代表增强相,则材料参数可表示为:σY01=250 MPa,E1=70 GPa,n1=0.455,h1=173 MPa,ν1=0.3,E2=440 GPa,ν2= 0.17.
其中:ν和E分别表示材料的泊松比和弹性模量.
对界面层而言,由于其力学性能测试比较困难,为了简化,可依据文献[16]假定界面层的力学性能参数满足基体的以下关系
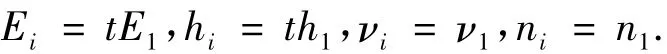
式中:i,1分别表示界面层和基体相,其他材料参数仍取自基体,换句话说,界面层也是各向同性的弹塑性体材料.系数t为界面层与基体的弹性模量之比,当t>1时,表明界面层的弹性模量比基体大,此时基体相有可能先发生塑性变形,此时界面称为强界面层;而当t<1时,表明界面层的弹性模量比基体小,此时界面称为弱界面层,在塑性变形时,其屈服行为可根据其相应的屈服准则进行判断.
2.3 边界条件
模型底边施加垂直方向的位移约束0,上边施加沿垂直方向的负位移,控制模型的变形量为10%,为了进一步控制变形的协调性,采用ABAQUS软件中的Equation命令,使模型在变形时,左右两个侧面沿水平方向的位移保持一致,这样就能保证变形中两个侧面始终平直.
2.4 数据处理
为了分析胞元模型所代表复合材料的流变应力,采用下式对有限元模拟结果进行处理.
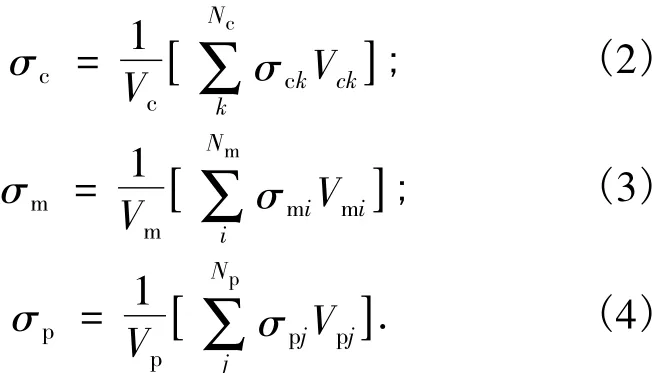
其中:σc为复合材料的流变应力,Vc为胞元中总的单元体积,Vck为胞元中的第k个单元体积,σck为第k个单元的平均流变应力,Nc为胞元中总单元数;σm为基体的流变应力,Vm为胞元中基体的单元体积,Vmi为基体中的第i个单元体积,σmi为基体中第i个单元的平均流变应力,Nm为基体的总单元数;σp为增强颗粒的流变应力,Vp为胞元中总的增强颗粒体积,Vpj为增强颗粒中的第j个单元体积,σpj为增强颗粒中第j个单元的平均流变应力,Np为增强颗粒的总单元数.
3 结果与分析
3.1 界面厚度对复合材料流变行为的影响
分别考虑无界面模型,以及界面层厚度分别为1、2、2.5 μm三种有界面层模型,并且界面层分别以弱界面和强界面两种形式来讨论.弱界面t<1,在此取t=0.5来计算;强界面t>1,在此取t=5来计算.为了能够详细说明变形中各部分的应力、应变场,以下分析以弱界面(t=0.5)为例分别讨论.
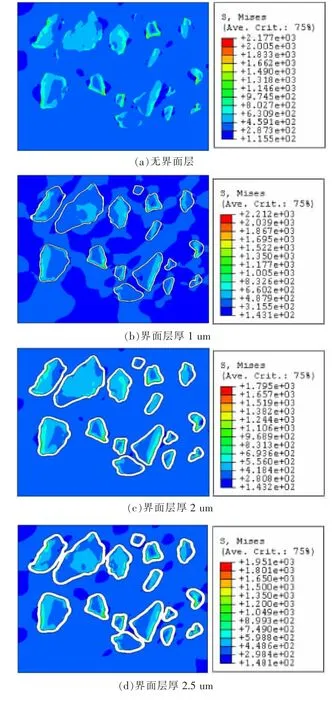
图3 复合材料等效应力分布/MPa
图3为变形程度为10%时的复合材料等效应力分布图,可以看出,无界面层时模型的峰值应力为2177 MPa,最小应力为115.5 MPa;界面层厚度为1 um时,峰值应力为2212 MPa,最小应力为143.1 MPa;界面层厚度为2 μm时,峰值应力为1795 MPa,最小应力为143.2 MPa;界面层厚度为2.5 μm时,峰值应力为1951 MPa,最小应力为148.1 MPa,从中可以看出,界面层的存在使模型的最小应力相应提高,峰值应力随着界面层厚度的增加,先减小后增加,这种变化可能与界面层的连接有一定关系.由图中可以看出,颗粒上的峰值应力多出现在尖角位置,这是由于材料变形时颗粒侧面的材料流动所形成的剪切力缘故造成的,并且大颗粒内部出现的应力分布存在一些差异,而小颗粒的应力分布并没有发生太大改变,另外,随着界面层的连通,基体中的应力分布先是不均匀分布,再均匀分布,最后又变化为不均匀分布,和应力的峰值变化完全一致.
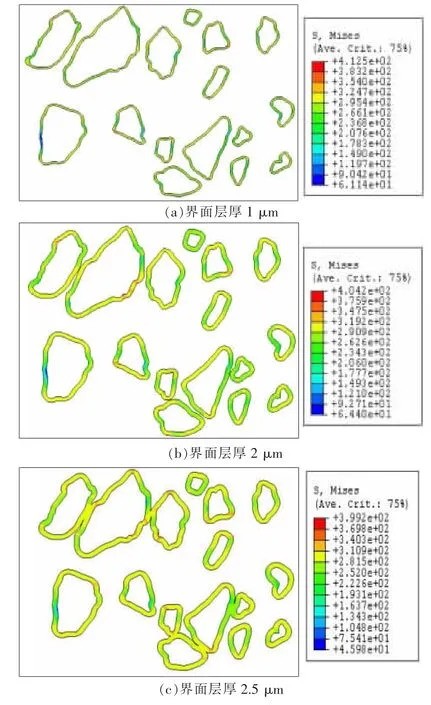
图4 界面层等效应力分布/MPa
图4为界面层的等效应力分布规律,可以看出,随着界面层厚度的增加,峰值应力在逐渐减小,而界面层厚度为1 μm和2 μm的最小应力相差不大,约为 62 MPa,但是当界面层厚度为2.5 μm时,其最小应力约为46 MPa,说明连通的界面对界面承载性有重要的影响,从云图分布来看界面厚度的改变并没有使界面层上的应力分布发生规律性变化,高应力区出现在界面的上方和下方,以及一些尖角的位置.
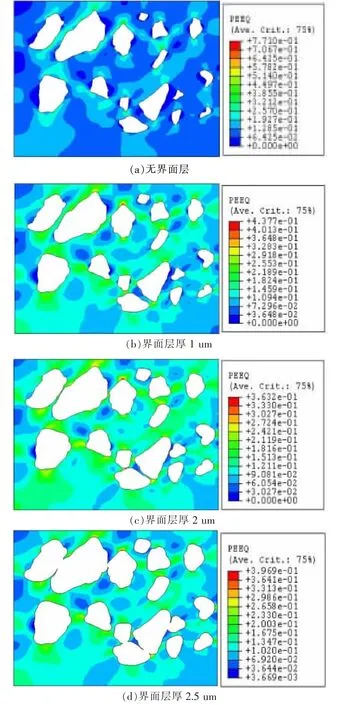
图5 基体等效应变分布
图5所示为基体的等效应变分布规律,可以看出,无界面层时基体的等效应变峰值约为0.77,其应变梯度较大;有界面层时,基体的峰值应变小了许多,约为0.4,从而应变梯度减小.从云图上看,无界面层时,高应变主要出现在颗粒的周围,但向基体内部过渡范围较窄,基体内部的应变分布相对来说比较均匀;而有界面层时,高应变区仍出现在颗粒周围,并向基体内部过渡的范围较广,但是随着界面层厚度的增加,颗粒周围的高应变区成片的连通起来.
3.2 界面厚度对复合材料强化性能的影响
根据式(2)—式(4),对变形程度为10%,弱界面层模型中基体和复合材料的流变应力进行计算,结果如图6(a)所示,可以看出基体的流变应力相差不大,数值差异在5 MPa以内,这说明界面层的存在以及厚度的变化对基体所承担载荷的大小影响不大;而复合材料的应力略有不同,有界面层时的流变应力比无界面层时要小,并且随着界面层厚度的增加,其流变应力没有太大变化.产生这种现象主要是因为弱界面层模型在受力时,由于界面层弹性模量小,先发生塑性变形,因此界面层就要吸收一部分变形能量,进而降低界面层对载荷的传递作用,使增强颗粒承担的载荷降低,因此弱界面复合材料在强度上就略低一些.而强界面的变化趋势与之不同,如图6(b)所示,可以看出,强界面层下基体的流变应力仍然在一个很小的范围内变化,而复合材料的流变应力随着强界面层的出现以及厚度的增加而增加,这是因为复合材料中的强界面层在受力后并不会率先发生塑性变形,变形的是基体材料,变形中基体会吸收大量的能量,从而使界面处的高应力得以释放或部分释放,界面不易被破坏,因此能够有效地把载荷向增强颗粒进行传递,使增强颗粒承受较大的载荷,从而使复合材料具有高的强度[12].
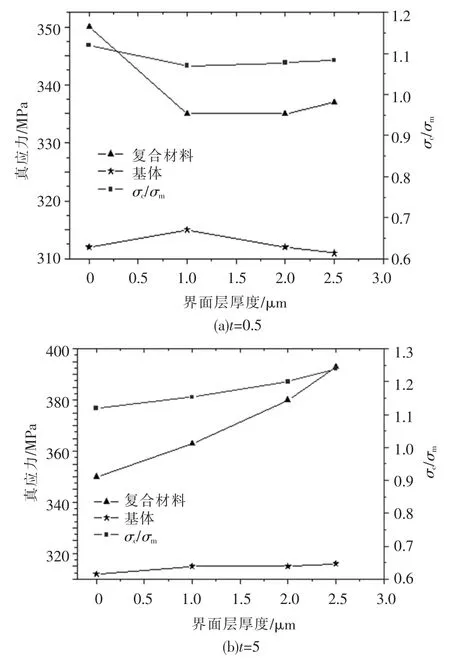
图6 界面厚度对复合材料流变应力的影响
颗粒增强金属基复合材料的强化主要来自于增强颗粒具有高的弹性模量而使载荷发生的转移现象.为了能够明确看出在弱界面层和强界面层下界面层厚度对强化效果的影响,分析中利用了表达式σc/σm,其中σc为复合材料的流变应力,σm为基体的流变应力.该比值高,说明复合材料中基体承担的载荷少,从而强化效果好,反之,则强化效果低.从图中可以看出弱界面层复合材料的强化效果低于无界面层复合材料,并且随着弱界面层厚度的增加,强化效果变化不大;而强界面层的复合材料强化效果要好于无界面层模型,并且随着界面层厚度的增加,强化效果也在增强,这说明界面层强度不同,界面层厚度对复合材料的强化作用存在差别.
3.3 界面强度对复合材料流变行为的影响
分析界面强度对复合材料性能的影响时,以厚为1 um的界面层为例,将界面层因子t分别取为0.5、0.8、2、5和10进行计算,并以界面层因子0.5和5为例,对比分析界面层强度对等效应力和等效应变分布规律的影响,如图7—图9所示.
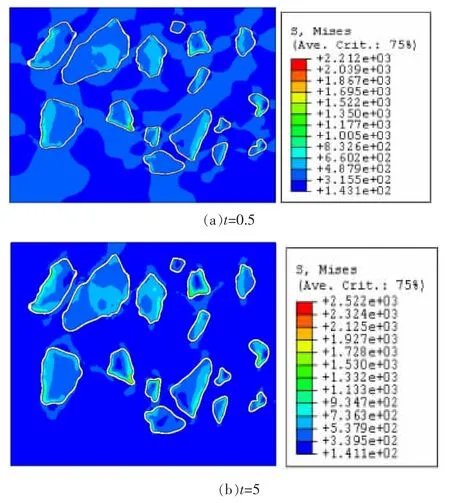
图7 复合材料等效应力分布/MPa
图7为复合材料的等效应力分布规律,由图可知弱界面层下的峰值应力为2212 MPa,最小应力为143.1MPa,而强界面层下的峰值应力为2522 MPa,最小应力为141.1 MPa,可以看出,随着界面层强度的增加,复合材料的应力整体提高,说明复合材料起到了颗粒增强的效果,从云图上看,弱界面层下基体中的应力梯度明显一些,而强界面层下基体中的应力分布非常均匀,并且可以看到颗粒中的高应力区仍出现在颗粒的尖角位置.
图8为界面层的等效应力分布规律,从图中可以看出弱界面层的峰值应力为约412 MPa,最小应力约为61 MPa;而强界面层的峰值应力约为767 MPa,最小应力约为127 MPa,说明界面层变强时,界面层承担的载荷会增加.从云图分布来看,峰值应力出现的位置仍在尖角.

图8 界面层等效应力分布/MPa
图9为基体的等效应变分布规律,可以看出弱界面层下的基体峰值应变约为0.43;而强界面层下的峰值应变则约为0.54,说明强界面层下基体的应变增加,应变梯度变大.从云图分布看,其高应变区基本都出现在颗粒的周围,并且界面越强,应变梯度也就越大,但分布均匀程度也有所减弱,这是因为当界面层的强度变大时,相当于增强颗粒加大,进而应力集中加剧,并且变形时先发生塑性变形的是基体材料,因此基体变形大而具有高的应变.
3.4 界面强度对复合材料强化性能的影响
根据式(2)—式(4),分别计算出变形程度为10%不同界面层强度下基体与复合材料的等效应力,如图10所示.从图中可以看出界面层厚度为1、2 μm时,基体的流变应力变化不大,而复合材料的流变应力随着界面层变强而变大,但是增加的幅度随着界面层强度因子的变化而不同,当t在1附近时,可以看出复合材料应力的变化斜率最大,呈明显的递增趋势;而当t大于1时,其增加量逐渐递减.
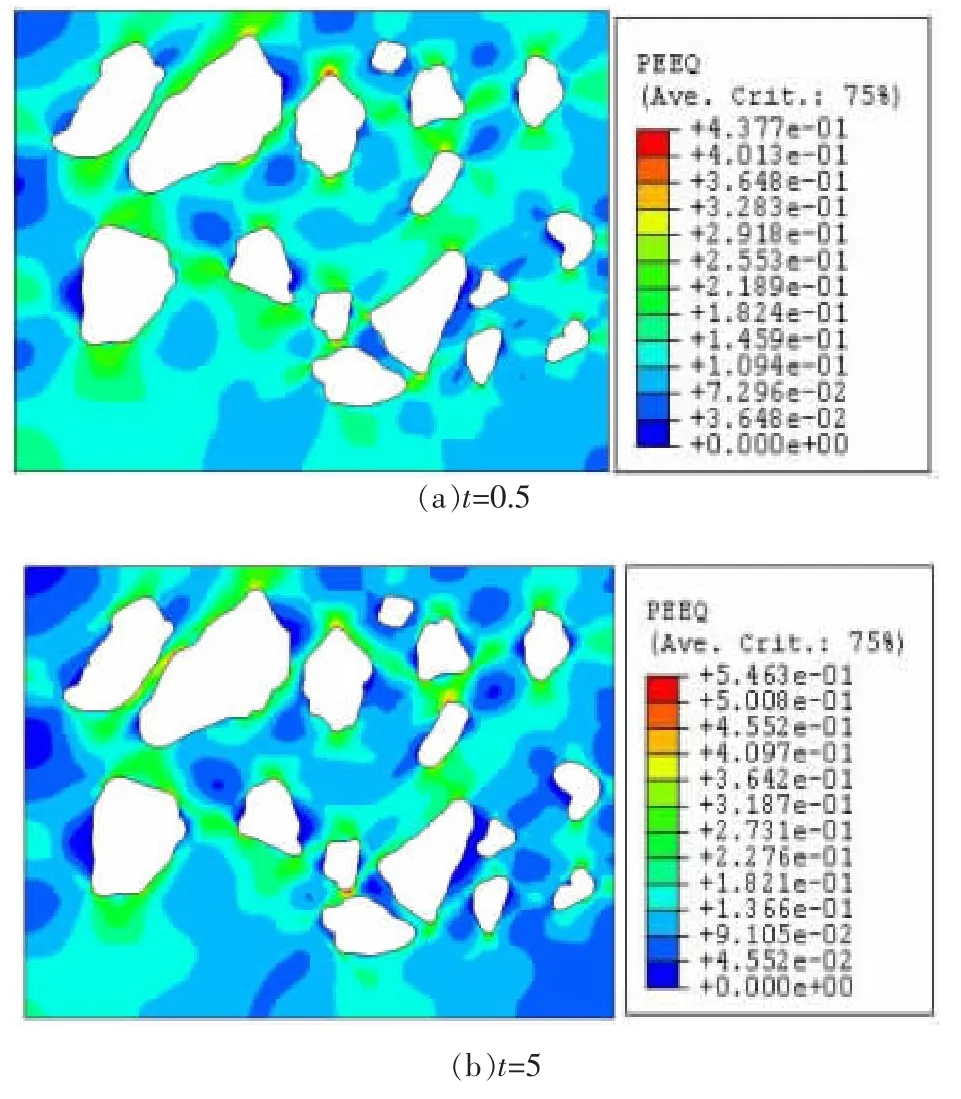
图9 基体等效应变分布
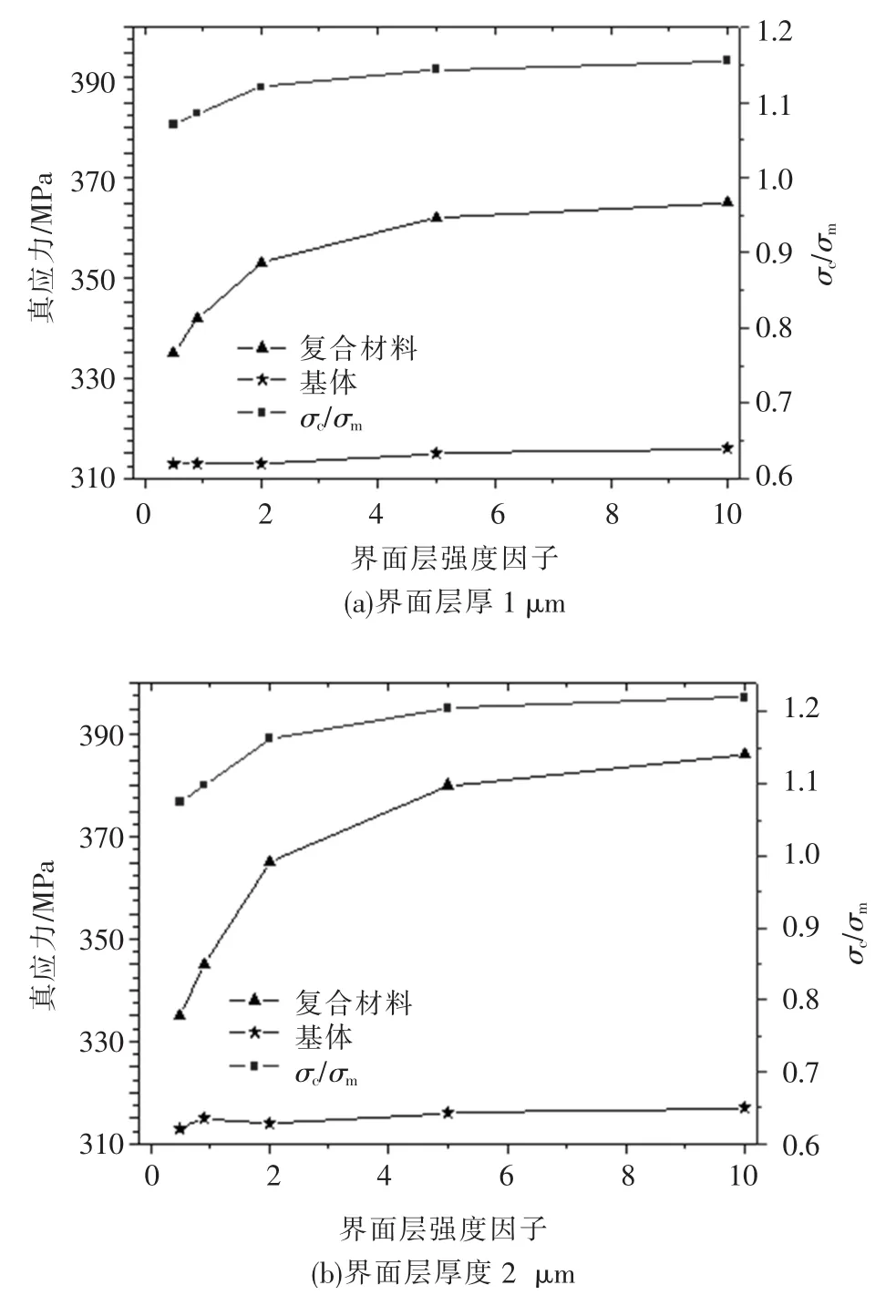
图10 界面强度对复合材料流变应力的影响
从强化效果来看,可以知道界面层越强,其强化效果越好;但是当界面层的强度与基体相差不大时,界面层强度每增加一点儿,其强化效果的增加量就非常明显;而当界面层强度远远超过基体时,其强化效果的增加量呈递减趋势.因此可以看出,界面层的模量并不是越高越好,当界面层强度已经能够保证界面紧密连接不被破坏时,界面模量只要适当就可以保证复合材料具有优良的力学性能.
4 结论
1)通过建立基于微观组织的胞元模型对颗粒增强金属基复合材料的界面行为进行了数值计算,在计算中获得了复合材料各组成部分的云图分布.
2)通过引入强化参数σc/σm,对界面层厚度以及界面层强度对复合材料性能的影响进行研究表明:在弱界面层下,随着界面层厚度的增加,复合材料的强化效果并不显著,而在强界面层下,随着界面层厚度的增加,强化效果非常明显;就界面层强度来说,界面越强,所表现出的强化效果就越明显,但当界面层强度比基体大的多时,随着界面层强度的增加,虽然复合材料的强化呈递增趋势,但是递增的幅度已逐渐降低.
[1]ONAT A,AKBULUT H.Production and characterization of silicon carbide particulate reinforced aluminumcopper alloy matrix composites by direct squeeze casting method[J].Journal of Alloys and Compounds,2007,436(1):375-382.
[2]DENG X,CHAWLA N,CHAWLA K K.Deformation behavior of(Cu,Ag)-Sn intermetallics by nanoindentation[J].Acta Materialia,2004,52(14):4291-4303.
[3]戴兰宏,凌中,白以龙.颗粒增强金属基复合材料变形强化中的应变梯度效应[J].高压物理学报,2001,15(1):5-11.
[4]SONG M,HUANG B Y.Effects of particle size on the fracture toughness of SiCp/Al alloy metal matrix composites[J].Materials Science and Engineering,2008,488 (1):601-607.
[5]ERGUN E,ASLANTAS K.Effect of crack position on stress intensity factor in particle-reinforced metal-matrix composites[J].Mechanics Research Communications,2008,35(4):209-218.
[6]RAMANATHAN S,KARTHIKEYAN R,GANASEN G. Development of processing maps for 2124Al/SiCpcomposites[J].Materials Science and Engineering,2006,441(1):321-325.
[7]CHENG N P,ZENG S M.Deformation behavior of SiC particle reinforced Al matrix composites based on EMA model[J].Transactions of Nonferrous Metals Society of China,2007,17(1):51-57.
[8]SEGURADO J,GONZALEZ C.A numerical investigation of the effect of particle clustering on the mechanical properties of composites[J].Acta Materialia,2003,51 (8):2355-2369.
[9]ALDAS K,MAHMUT D.Experimental and theoretical analysis of particle distribution in particulate metal matrix composites[J].Journal of Materials Processing Technology,2005,160(3):289-295.
[10]BOSELLI J,GREGSON P J.Quantification of particle distribution effects on fatigue in an Al-SiCpcomposite[J].Materials Science and Engineering,2004,379 (1):72-82.
[11]陈尚平,解念锁.非连续增强铝合金复合材料的力学性能[J].材料科学与工程,1997,15(4):72-78.
[12]郭成,程羽,尚春阳,等.SiC颗粒增强铝合金基复合材料断裂与强化机理[J].复合材料学报,2001,18 (4):54-57.
[13]李子全,吴炳尧.不同冷却条件下的SiCp/ZA-27复合材料界面的TEM观察[J].南京大学学报:自然科学版,2001,37(1):84-90.
[14]LEE J C,AHN J P.Control of the interface in SiC/Al composites[J].Script Materialia,1994,41(8): 895-900.
[15]王锦程.复合材料阻尼性能的数值模拟[D].西安:西北工业大学,2001:36-37.
[16]ZHANG W X,LI L X,WANG T J.Interface effect on the strengthening behavior of particle-reinforced metal matrix composites[J].Computational Materials Science,2007,41(2):145-155.
Interfacial effects on the strengthening behavior of metal matrix composite reinforced with SiC particles
ZHANG Peng,LI Fu-guo
(School of Materials Science and Engineering,Northwestern Polytechnical University,Xi’an 710072,China,E-mail:fuguolx@nwpu.edu.cn)
The interface in a metal matrix composite was modeled using finite element method to study the effect of interface on the metal matrix composite,such as interface thickness and stiffness.The finite element model was established based on the actual microstructure,including the modeling without interface,the modeling with interface and the modeling with connective interface.In the analysis,the special attention was put on the distribution of mises in matrix,interface and particles.The results show that under the soft interface,the influence of interface thickness on the mechanical behavior is not distinct,while under the strong interface,the influence of interface thickness on the mechanical behavior is obvious.The intensity of metal matrix composite increases with the increasing interface modulus,but the extent of increase is decided by the modulus matching between interface and matrix.
metal matrix composite;interface;strengthening behavior;cell model
TB331文献标识码:A 文章编号:1005-0299(2010)02-0192-07
2008-07-20.
航空基础科学基金资助项目(03H53048).
张 鹏(1977-),男,博士研究生;
李付国(1965-),男,教授,博士生导师.
(编辑 魏希柱)
- 材料科学与工艺的其它文章
- 包覆成孔剂法制备高性能多孔氮化硅陶瓷工艺

