过程强化装置的偏心转子与活塞的接触方式对设备运行的影响＊

朱瑞林 朱国林

(湖南师范大学工学院) (江西公安专科学校))

过程强化装置的偏心转子与活塞的接触方式对设备运行的影响＊

朱瑞林＊＊朱国林

(湖南师范大学工学院) (江西公安专科学校))

探讨了过程强化装置的偏心转子与活塞点接触时,设备在运行过程中长度与压力的变化规律;并提出了消除这种变化的措施。

过程强化 偏心转子 压力

0 前言

要产生振荡运动,可利用偏心转子。作为一种机械装置,偏心转子可用于许多机器设备中。但不论是现有技术或理论,都没有注意到偏心转子实际上只保证其圆心在某个方向作简谐振动,某些情况下并不能保证由转子驱动的构件 (如活塞)作同样的简谐振动以及由此引起的相关问题,如由转子驱动的两活塞内端面之间的距离不能保持恒定从而影响设备内介质的压力、不能消除转子因倾斜造成的椭圆度影响等。本文研究一种改进的转子机构,其特点是:必要时可使由转子驱动的构件 (如活塞)作与转子中心同频率 (周期)、同振幅的简谐振动,并使由转子驱动的两活塞内端面之间的距离保持恒定,从而消除对设备内介质压力的影响。

1 塑性区深度的讨论

图1所示的是利用转子机械装置驱动活塞以产生振荡运动的一种过程强化装置,其技术方案是[1]:在过程设备 1(内设挡板 2)上设置与之密封配合的转子机械振荡装置,使过程设备内的流体形成湍流或充分混合,以强化工艺过程。振荡装置主要由活塞 3与圆柱转子 4构成,转子对称斜置,形成相位差 180°的偏心距,此即活塞振幅。将转子横截面绘于图 2,由图 2不难推得点接触 (即活塞杆直接或通过接触球 7与转子接触)时,在任意时刻,左活塞的位移是:

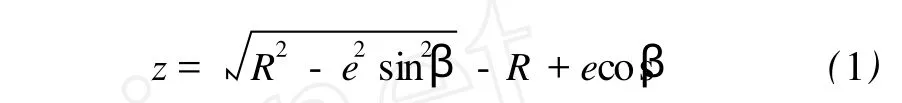
式中 z——活塞杆末端与转子的接触点 i到活塞位移为 0的平衡线 0-0的距离,即为活塞内端面的行程;

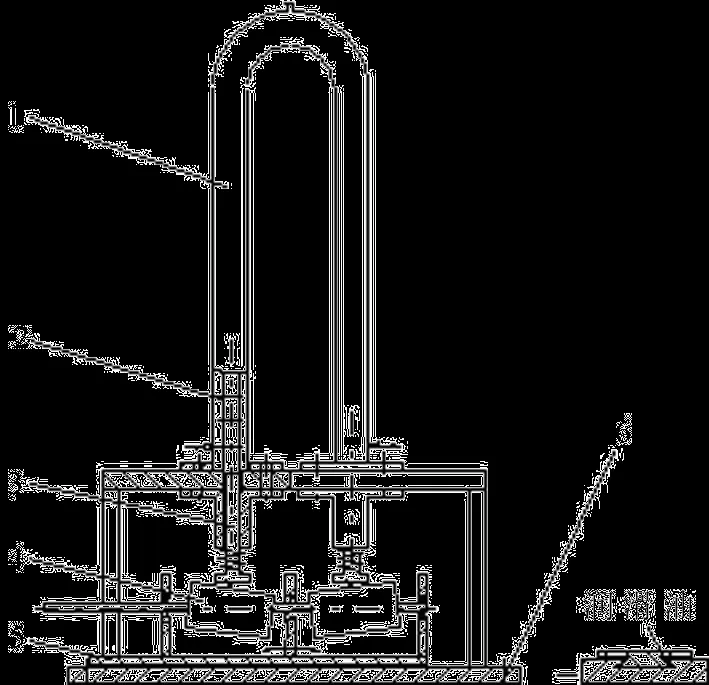
图1 过程强化装置

图2 左转子从使活塞处于最高位置旋转到使其处于最低位置的横截面

R——转子横截面半径;

e——转子偏心距;

β——转子位置角度;

同理,点接触时在任意时刻右活塞的位移是

显然式(1)、式(2)均不是简谐运动 ecosβ。

经研究得知,只有转子顶点 d(参阅图 3)的位移是简谐运动 ecosβ。为了让这一简谐运动传递给活塞,经分析,发现需要加一切线,即在活塞杆末端增加一接触件 8,如图 3(b)所示,使接触件与转子的横截面相切,而接触件的增加并没有使结构复杂起来。加接触件后,活塞的位移才是 ecosβ[2],它与未加接触件时 (通过接触球与转子接触,即点接触)的位移实际上不同,有一差距 ,如图 3所示。

图3 点接触与切线接触的比较

只有加了接触件后,活塞的位移才是简谐运动ecosβ;只有活塞的位移是 ecosβ,才能保证设备体积不变,从而保证设备内流体的体积在设备运行过程中始终保持不变。分析如下:

参阅图 2、图 3,在任意时刻 (任意位置)时,切点 d点到 0-0线的距离,即加切线时左活塞的位移为 z=dk=cd-R=oc+od-R=oc=ecosβ。此时右活塞的位移必为 z′=-ecosβ(注意,两转子对称斜置),故在任意时刻左、右活塞行程之和为 0,不会引起设备长度的变化。点接触则不然,此时令左、右活塞行程之和

若右活塞上升或下降的距离等于左活塞下降或上升的距离,则Δ应为 0,所以Δ实际上也是任一时刻不同λ下两活塞内端面间的距离变化。显然Δ并不恒为 0,这表示当转子与活塞点接触时,由于左、右转子并不各自以简谐振动规律运行,故二者的位移并不完全对称。由式 (3)知,Δ<0,这表示对图 1所示的结构,机构运行过程中两活塞内端面间的距离始终略呈增大状态,不会引起设备内介质的压力增加,但会引起压力降低,适用于设备空间可略有增大的场合或空间的增大对过程影响不大的场合;对不允许设备内的压力减小的场合会有一定影响。若要使运行过程中两活塞内端面间的距离呈缩小状态,只需相应地改变转子截面的几何形状。式 (3)还表明Δ以 90°为对称,并在β=90°处为最大值 (负的),以 180°为周期。令

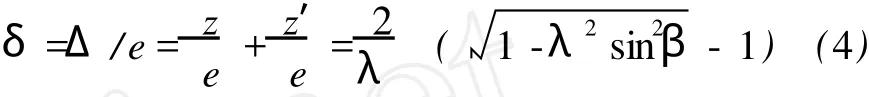
一些λ任一瞬间β处的δ如图 4所示,δ也是受λ影响的,λ越大,即偏心距越大,δ越大。要改变δ的大小,需调节λ。以 R=80 mm为例,设λ=0.5,于是 e=λR=40 mm,β=90°处Δ=δe=-0.5359×40=-21.4 mm,又设设备长度 L=2000 mm,Δ/L=21.4/2000=1.07%,设备长度有一个百分点的增长。

图4 一周内δ受λ影响的规律

2 Δ和λ对压力的影响

设备在运行过程中不能保证体积始终不变会有什么不良后果呢?因为流体的体积变化,就会引起其压力发生变化,压力变化不仅影响设备的正常运行,而且影响产品的质量和生产效率,特别是对压力敏感的产品的生产,影响是严重的。下面讨论由于设备长度变化导致体积变化所引起的压力变化,以理想气体为例,实际流体可以此作为参照。根据气体体积与压力的关系[3]有:

式中 p0——初始状态的压力

p1——设备运行过程的压力

V0——初始状态的体积

V1——设备运行过程的体积

由式 (5)得压力降低系数为

由式 (7a)显然可知,λ、η越大,压力降低得越多。为了详细看出λ、η对压力的影响,将λ、η对m的影响规律例出如图 5所示,也便于工程上的查图。

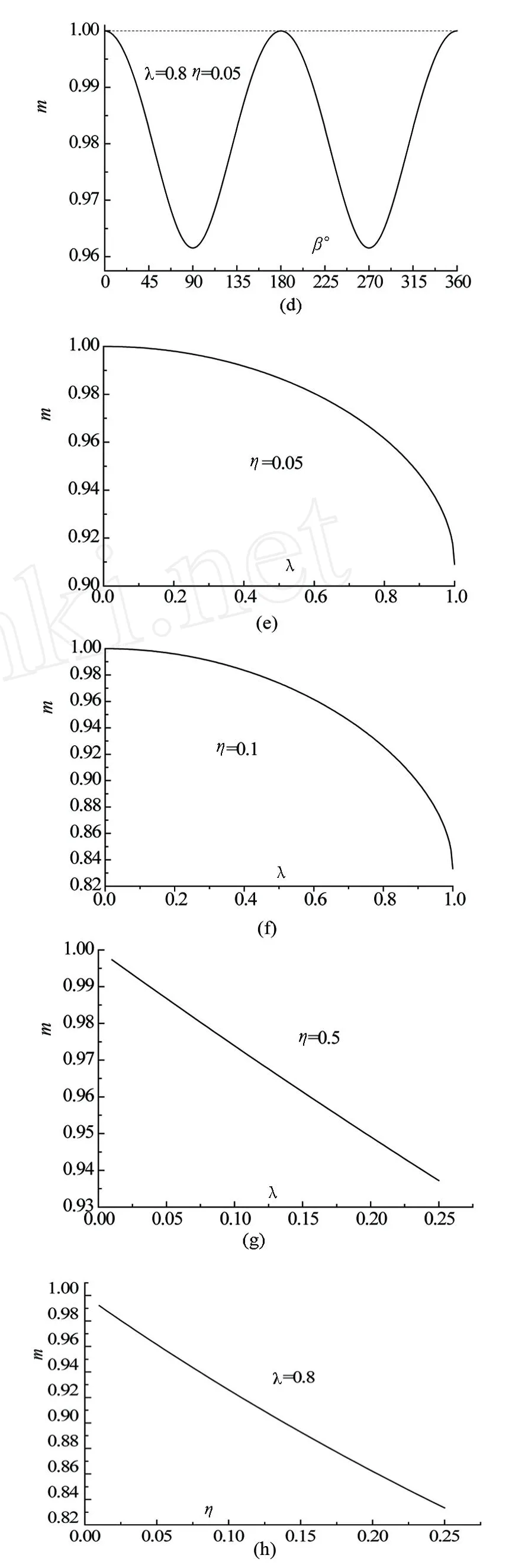
图5 λ、η对 m的影响规律

就图 5所示的几个实例,压力降最多时,可达到 15%,所以在活塞杆末端加一与之垂直的接触件很有必要。

3 结论

转子与活塞杆端部点接触时,由转子推动的活塞的运动不是纯简谐运动,这将使得设备运行过程中其长度有所变化,从而引起设备内流体压力的变化。为使设备在运行过程中其长度恒定,可在活塞杆端部设置与活塞杆垂直的接触件,使接触件与转子成切线接触,这样即可保证由转子推动的活塞作纯简谐运动,从而消除设备运行中流体压力的波动。

点接触时,设备内流体压力的波动呈周期变化,以π为周期;压力变化的大小与转子偏心距(λ=e/R)和设备长度 (η=R/L)有关,λ、η越大,压力降低得越多。本文给出了λ、η对压力的影响规律示图。

[1] 朱瑞林.一种工艺过程流体强化装置 [J].石油化工设备,2006,35(1):68-71.

[2] 朱瑞林.一种转子机械装置 [P],中国专利:2006100843262.

[3] 韩德刚.物理化学 [M].北京:高等教育出版社,2009.2.

＊国家科技部创新基金资助项目,编号:09C26214305047。

＊＊朱瑞林,男,1962年生,博士,教授。长沙市,410081。

2009-12-28)