考虑资源共享的维修过程建模及资源配置研究

曲长征，王松山，高鲁

（军械工程学院，河北 石家庄050003）

维修资源是完成装备维修任务的物质基础，现代维修管理对维修资源的科学配置提出了越来越高的要求。部队维修过程中一般以小组包修的形式完成，检测设备等大型设备在各装备并行维修过程中共享使用，维修人员与检测设备的合理配置是发挥维修机构整体效益的关键。当前研究中，针对维修过程的排队问题分析一般可分为两种：一是以维修小组或修理工作为服务台进行研究，忽略设备的使用问题[1，2，3，4，5]；二是以大型设备作为服务台，忽略人员的影响[6]。显然，这两种方法都难以从人员和设备综合的角度研究资源优化配置问题。

本文结合部队维修机构实际，综合考虑维修小组和检测设备在维修过程的应用，建立多小组共享检测设备的过程模型，研究不同配置情况下的系统性能，从而对资源配置方案进行分析评价。

1 维修过程中的资源运用分析

部队修理机构在完成修复性维修任务时一般采用小组包修的形式。但在维修任务需求的所有资源中，部分资源不作为维修小组的独占资源，而是在各组之间交替使用，包括具有高级技术职务的人员和配置较少的专用设备，如故障检测设备或大型分解设备。它们在维修过程中一般不是全程都使用，而只是用于完成阶段性的维修作业。可以认为它们不属于特定的维修小组，而是属于共享资源。共享资源在维修过程中应交叉、轮流使用，当使用发生冲突时，会有产生等待现象。

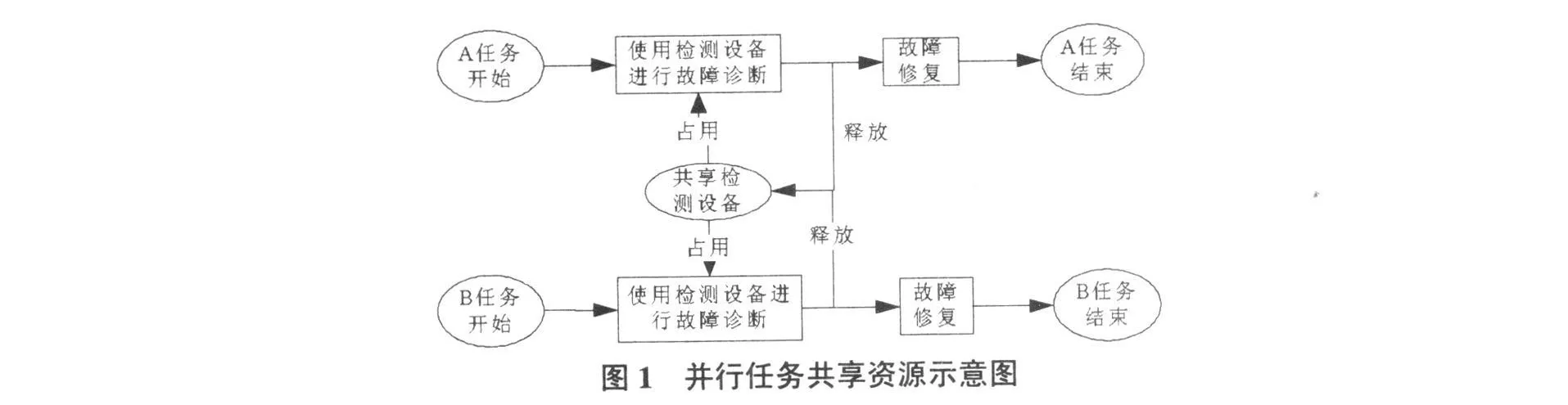
例如，故障诊断所需资源除必要的人员外，一般还需要检测设备，而故障定位后的故障修复过程则不再需要检测设备。以两任务并行维修过程为例，其共享检测设备的过程如图1所示。

A、B任务开始维修的条件还包括必须有空闲的维修小组，维修过程开始后一直占用维修小组，直到任务结束才释放，图1中略。

2 维修过程建模

对于上文分析的维修资源占用和释放过程，采取排队网络分析方法是非常困难的。该情况下，整个维修过程中参与的资源是变化的，难以定义确定的服务台数量。而如果将故障诊断和修复过程区分为两类服务台，维修小组又同时参与到两类服务台中，仍无法定义服务台数量。鉴于此，本文采用Petri网建模技术对该服务过程进行形式化建模，然后依托Petri网定性定量分析技术进行分析。

本文采用常量弧Petri网进行建模，其定义如下。

2.1 库所变迁网定义

一个库所变迁网（P/T网）是一个四元组N=（P，T，DPre，DPost），其中，P是一个有穷集合（N的库所集合），T是一个有穷集合（N的变迁集合），并且和P不相交，DPre，DPost∈IN|P|×|T|是矩阵（网N的向前和向后关联矩阵）。

库所变迁网N的标识是一个向量m∈IN|P|，IN={1，2…}。网N和标识m0（初始标识），称为库所变迁网系统S=（P，T，DPre，DPost，m0）。如果m≥DPre[◦，t]，则变迁t∈T在标识m下具有发生权，表示为m，变迁规则为：m′=m+DPost[◦，t]—DPre[◦，t]。相关术语参见文献[7]，不赘述。

2.2 维修过程Petri网建模

考虑单类任务时，采用Petri网建立的维修过程模型如图2所示。

图2模型中rt表示空闲修理小组，m0（rt）=Nt，re为空闲检测设备，m0（re）=Ne。与资源库所相连的连接弧DPre=DPost=1，表示为任务占用和释放的资源数量为1。

t1为开始维修；t2为故障检测，时间延迟为检测时间d1；t3为释放检测设备，t4为故障修复，时间延迟为修复时间d2；t5为释放维修小组。

t1的使能条件是m（rt）≥DPre（rt，t1）=1并且m（re）≥DPre（re，t1）=1，即维修小组和检测设备都有空闲。使能条件满足后即可触发t1，触发规则为：

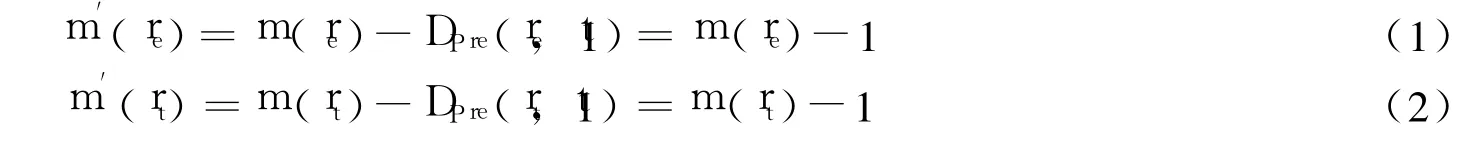
即空闲维修小组和检测设备减1，同时消耗p1中令牌（Token）并输出到p2。如果t1不满足使能条件，即当前空闲资源不满足任务要求，则p1中的任务令牌处于等待状态。故障检测后t3触发释放检测设备，即re库所令牌加1，故障修复后释放修理小组，rt库所令牌加1。

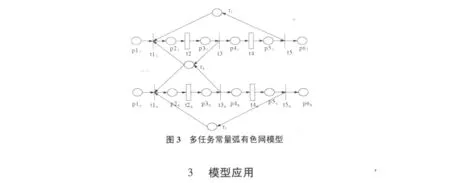
考虑多类任务时，不同任务的模型的网结构相同。通过共用资源库所将不同的网模型融合可形成类任务的系统模型，图3显示了n种类型任务共享资源的系统模型。模型中，不同任务的过程模型有相同的网结构，以不同的下标{1，2…，n}进行区分。

3.1 定性分析

系统状态变化可以用Petri网的进程来分析。状态与变迁并重，把系统中发生的变化和引起的状态改变如实的记录下来，就是系统的进程。进程如实描述Petri网系统中所发生的一切的观察记录，它比较直观地反映了系统中变化的顺序和并发关系，描述了系统中“冲突”的消解过程。一个进程只是网系统行为的一次记录，系统所有的进程的集合才是网系统动态行为的完整描述。

以两任务共享一个检测设备并行维修为例，首先我们假设维修小组数量无限多，忽略维修小组库所，其进程如图4。

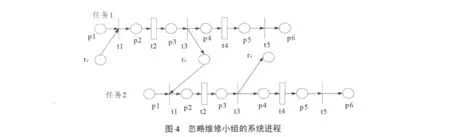
从总体上，两任务可同时进行维修。两任务在进行故障检测（t2）时，受re的限制，必须串行使用，不能同时并行触发。对re的需求不冲突时（p1中有令牌时，re中有令牌），则串行使用不影响维修过程，反之，则产生等待。p1到t1触发的等待时间即为等待检测设备时间。

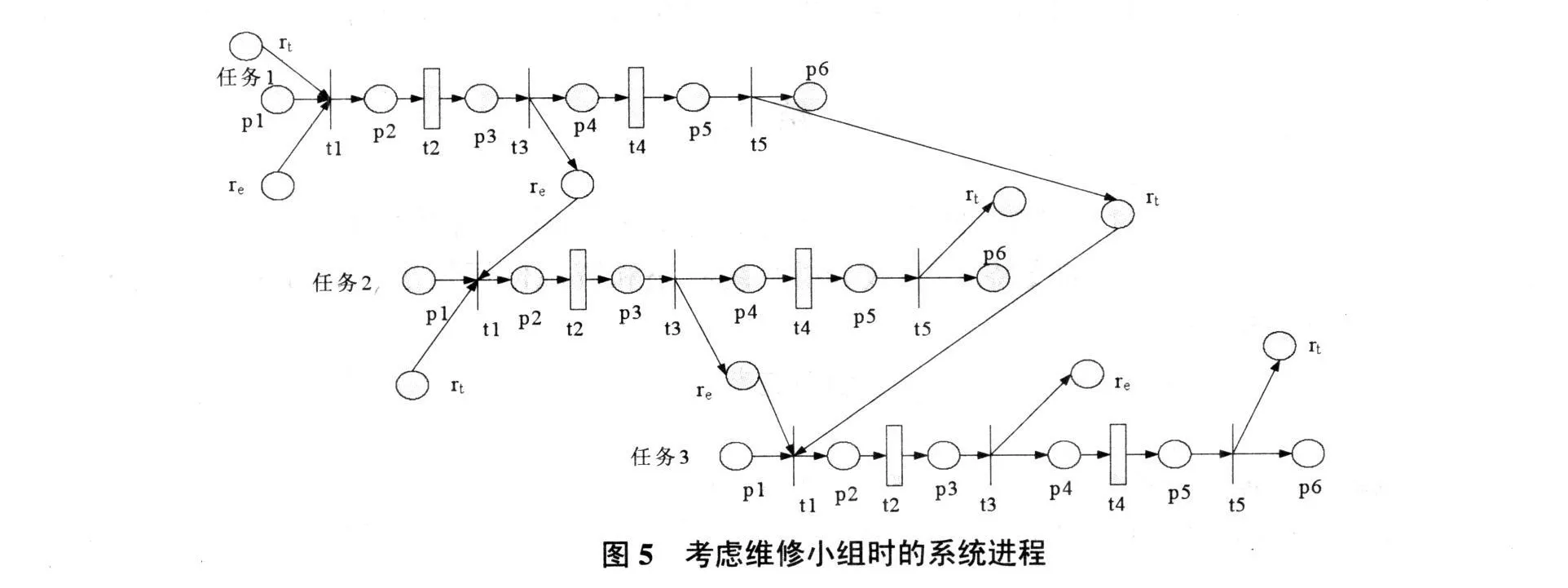
当考虑维修小组数量的实际影响时，系统进程中则要体现库所rt。以2个修理小组共享一个检测设备为例，系统的进程如图5。

图5中，任务3维修开始的条件：不仅包括任务2释放检测设备，而且要在任务1或任务2释放维修小组（图中进程为任务1释放）。如果rt先出现，而re未出现，则表现为等待共享检测设备；如果re先出现，而rt未出现，则表现为等待维修小组。如果re、rt同时出现（同步），不用相互等待，两种资源的利用率也会趋于一致，检测设备与维修小组搭配合理。

3.2 定量分析

令牌从p1到p6所经历的时间即为任务完成时间。当时间延迟为指数分布时，Petri网模型可转化为马尔科夫链，通过解析方法分析系统性能。当时间延迟为任意分布时，可采用Petri网仿真分析软件进行分析，如ExSpect。基于ExSpect的组件重用机制，笔者建立了维修机构领域模型库[8]，提高了建模与仿真效率。

3.3 实例研究

某维修单位担负某类装备的维修任务，装备故障间隔时间服从指数分布，平均间隔时间0.8h。任务可分为5种类型，故障检测时间服从指数分布，故障修复时间服从正态分布，属性参数见表1。

表1 任务参数

资源配置方案为：3个维修小组和1套故障检测设备。采用Petri网分析工具ExSpect对模型进行仿真。经分析系统可以达到稳态，于是采用稳态分析方法，系统性能见表2。

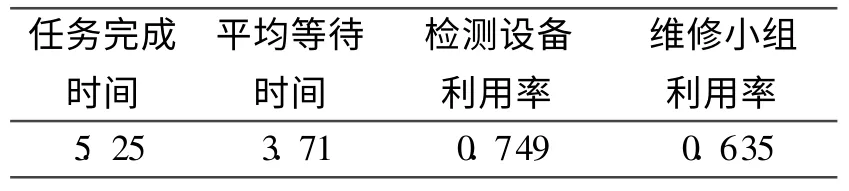
表2 系统性能参数

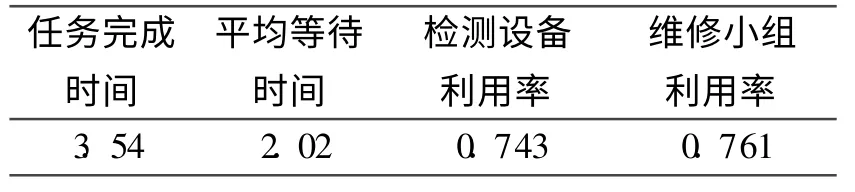
表3 改进后的系统性能参数

从仿真结果可以看出，检测设备的利用率比维修小组的利用率高，说明由检测设备占用造成的装备等待维修占多数。从原理上，可以从减少维修小组或增加检测设备入手，增加维修单元的整体资源利用率。经仿真分析，该例中增加一个检测设备和减少一个修理小组都使利用率的差异变大，即匹配关系变得不好。

考虑将两个维修单元合并，并减少一个修理小组，即5个修理小组和2个检测设备合成一个大修理单元，同时将两个修理小组的任务合并，即频率加倍。仿真结果见表3。

仿真结果表明，在维修小组与检测设备5∶2的比例配置下，资源利用率达到均衡，即达到最佳匹配关系。其中，任务完成时间的大幅减少是由于两个修理单元合并后，形成的多服务台结构使服务效率提高。

4 结 论

基于Petri网建立的维修过程模型，图形显示与数学定义并重，支持对系统进行定性分析，应用Petri网模型进行仿真分析有成熟软件的支持，可有效分析系统状态和资源使用情况。Petri网模型的定量数学分析方法有待进一步深入研究。

1 叶宗文.维修行业中排队模型的应用[J].四川兵工学报，2009，30（10）：65—67.

2 喻春明，迟玉红，方艳东.排队系统的非平衡动态指派模型及战时维修应用[J].东北大学学报（自然科学版），2008，129（11）：1617—1620.

3 肖慧鑫，李耀光.排队维修模型在武器系统可靠性分析中的应用研究[J].火力与指挥控制，2008，33（3）：135—142.

4 郭勇，黄党红.基于排队维修模型的武器系统可靠性分析[J].战术导弹控制技术，2005，（2）：88—90.

5 黄大明，黄世伟，覃频频.汽车维修排队系统的确定与优化[J].广西大学学报（自然科学版），1998，23（4）：388—340.

6 马惠.排队模型在多服务台设备维修管理中的应用[J].设备管理与维修，2009，（10）：14—16.

7 CLAUDEGIRAULT.系统工程Petri网——建模、验证与应用指南[M].王生原，余鹏，霍金键，译.北京：电子工业出版社，2005：30—33.

8 曲长征，张柳，于永利，等.基于ExSpect领域模型库的装备维修机构仿真环境构建[J].系统仿真学报，2009，21（9）：2772—2776.