货币增长不确定性与通货膨胀不确定性——“波动溢出”假说与实证检验

苏梽芳,胡日东

(华侨大学数量经济研究院,福建泉州362021)

一、引 言

经济社会发生较高通货膨胀时,通货膨胀预期一般趋于更加不稳定,这已成为研究者公认的特征事实,这种特征事实同时也被称为通货膨胀——通货膨胀不确定性关系。从目前已有的文献看,虽然学者对通货膨胀——通货膨胀不确定性关系持不同观点,但大多认为通货膨胀不确定性与货币政策冲击关系密切。然而在实证研究方面,一般都是将两者分开单独研究,对两者的关联研究极少,从而割裂了两者的联系。因此,研究货币增长不确定性与通货膨胀不确定性的关系,不但对理解货币当局行为如何导致通货膨胀不确定性具有重要的理论意义,而且对于决策层在目前全球经济可能再度发生通货膨胀的背景下如何进行通胀预期管理,避免自身行为成为经济波动的根源也具有重要的现实意义。

本文的研究动机与思路受两方面文献的启发:一方面,货币增长率与通货膨胀率之间的关联,作为货币经济学的核心问题已积累了大量文献,然而大多数文献只考察货币增长与通货膨胀的一阶矩关系,关于两者二阶矩关系的研究却极为少见。而两者的二阶矩,恰恰是货币增长不确定性和通货膨胀不确定性的合适度量。随着二阶矩计量模型的发展,为了充分发掘货币增长率和通货膨胀率之间蕴含的丰富信息关系,可以通过它来研究两者之间的“波动溢出”关系。另一方面,金融市场之间“波动溢出”效应检验的文献提供了可行的研究思路与方法。金融市场的研究者认为,一个资本市场的收益和波动不仅受到自身过去几期滞后的影响,还可能受到其他资本市场的制约,即市场间可能存在“波动溢出”或者说Granger因果关系,而被用于检验“波动溢出”效应的模型一般是多元GARCH模型。我们认为关于货币增长不确定性与通货膨胀不确定性的“波动溢出”关系同样可以在多元GARCH模型分析框架下进行研究。

相对于现有文献,我们试图在以下几方面有所拓展。首先在归纳关于通货膨胀与通货膨胀不确定性关系理论研究的基础上,提炼出货币增长不确定性向通货膨胀不确定性“波动溢出”的计量检验假说。其次在计量方法方面,应用多元BEKK-GARCH模型对假说进行实证检验,这种方法既度量了货币增长不确定性与通货膨胀不确定性,又避免了单变量GARCH模型无法充分利用变量之间信息的缺陷。同时在向量分析框架内,我们可以进行系数约束估计,从而实现“波动溢出”效应的检验,避免了使用“两步法”所遭受的“Pagan批评”。最后,以往研究往往只注重货币增长与通货膨胀水平之间的相互影响,这是一种静态的描述。然而,两个序列之间存在的一阶矩关系可能是虚假的,因为在进一步考察它们之间的高阶矩关系之后,这种一阶矩关系往往会消失(Lutkepohl,1993)。因此,研究货币增长率与通货膨胀率时间序列的二阶矩,既避免了上述缺陷,又丰富了货币增长率与通货膨胀率关联方面的文献。

二、相关理论回顾与假说提出

提出货币增长不确定性和通货膨胀不确定性之间的“波动溢出”效应的理论依据是关于通货膨胀——通货膨胀不确定性关系的大量理论研究。货币当局在两者的逻辑关系中扮演了重要角色,其行为假设常成为研究两者关系的切入点。

一部分研究主要突出了货币政策的不确定性对通货膨胀不确定性的影响。Cukierman和Meltzer(1986)认为通货膨胀和通货膨胀不确定性之间联系的主要根源在于货币当局行为的不确定性。他们指出,当公众存在对货币政策的不确定性时,更容易引发货币当局利用通货膨胀来刺激产出增加,因此导致了平均通货膨胀率的上升；而较高的通货膨胀率将引发公众对未来货币政策不确定性的增加,因为公众不清楚货币当局将会进一步刺激产出还是牺牲经济增长以抑制通货膨胀,进而引发了对通货膨胀预期的不确定性。Ball(1990)进一步明确了公众对货币当局行为产生不确定性的原因是他们不清楚货币当局的类型。Ball将货币当局分为保守型和开放型两类,保守型货币当局不愿承受抑制通货膨胀带来的失业成本,开放型货币当局则不会考虑失业成本。当通货膨胀水平很低的时候,两类货币当局都愿意维持通货膨胀水平；而当冲击提高了通货膨胀水平时,公众无法判断货币当局此时的类型,由此产生了通货膨胀不确定性。

另一部分研究突出了货币政策效果不确定性对通货膨胀预期的影响作用。Friedman认为货币政策的效果有“长而多变的(Long and variable)”时滞的特点,货币政策作用时间与功效的不确定性,使得货币政策在企图稳定产出波动时,不能达到预期的目标。Holland指出,由于市场价格体系中存在各种各样的定价策略,货币存量的变化对不同价格的影响是不同的。当发生未预期货币存量变化时,有些价格会相应地瞬间变化,有些价格的变化则需要一段时间。正是由于市场上存在不同粘性的价格水平,公众不能确定货币政策变化的效果进而影响了预期,因此产生了通货膨胀不确定性。这个分析的逻辑结论是:即使货币当局的行为是确定性的,但是由于货币增长对价格水平的影响存在不确定性,仍然会产生通货膨胀不确定性。

还有一部分研究则强调经济发展过程中货币政策机制变化所导致的通货膨胀不确定性。Friedman(1977)最初提出了这个观点,他认为货币政策机制变化是过去所观测到的通货膨胀与通货膨胀不确定性正相关关系一个潜在的、可能的解释。Evans和Wachtel(1991)秉承了Friedman的观点,他们将通货膨胀不确定性分为两个部分,其中一部分是由货币政策机制不确定性所引发。其定义是指公众可能对货币当局的政策机制的特点以及未来政策机制如何变化产生不确定性进而导致对未来通货膨胀的不确定性。

理论是需要检验的。在前面所回顾的理论研究中,实际上具有许多方面的经济计量检验内涵。而我们关注的焦点是:是否存在货币增长不确定性向通货膨胀不确定性“波动溢出”的效应,而这一点恰恰为后来的实证研究所忽略。究其原因,以往理论研究只把货币当局行为假设作为解释通货膨胀——通货膨胀不确定性关系的切入点。即使是Holland(1993)的研究,由于受制于计量方法,也只是考察了货币政策效果的不确定性如何导致通货膨胀不确定性。实际上,无论是货币政策当局行为的不可预测性,或是货币当局类型不确定性抑或是偏好冲击信息的私有性,还是货币政策机制变化所导致的不确定性,在实证研究中,往往都是通过一个变形后的货币增长方程来分离出各种不同来源的不确定性。基于对上述文献的讨论与认识,我们提出关于货币增长不确定性和通货膨胀不确定性之间关系的一个计量检验假说:

通货膨胀不确定性是其他隐藏的宏观经济不确定性的综合结果,其中最直接、最重要的因素是货币政策。货币当局行为、货币政策效果和货币政策机制变化等方面的波动信息影响了公众的预期,加剧了公众通货膨胀预期的不稳定性。即存在货币增长不确定性向通货膨胀不确定性“波动溢出”的效应。

三、BEKK-GARCH 模型分析

ARCH模型是考察单个市场资产收益波动的一个有力工具,单变量ARCH模型能够充分刻画单个金融市场波动的时变特征,然而在考察多个资产波动的相关性方面却缺乏效率,为了研究多个收益率序列之间波动的相关性,Bollerslev等(1988)提出了Vech形式的多元GARCH模型。但由于这种设定形式会使参数较多、估计存在困难,因此实际中往往对该模型予以对角形式简化。这种简化减少了待估参数,符合计量模型的简约原则,但无法考察变量之间的“波动溢出”关系。为避免以上缺陷,本文中我们使用如下BEKK设定形式:

式(1)可以分开表述为:

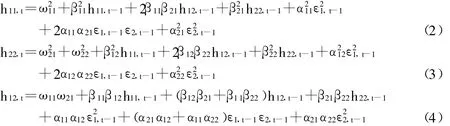
其中:C为常数上三角矩阵；A代表ARCH项的系数矩阵；B代表GARCH 项的系数矩阵；ωij、αij、βij分别为矩阵 C、A、B 的第(i,j)个元素 。

在此模型中我们可以通过估计参数得到通货膨胀率与货币增长率的条件方差,即得到我们感兴趣的通货膨胀不确定性序列h11,t与货币增长不确定性序列h22,t。更进一步我们通过对αij、βij(i≠j)值施加约束条件,实现对“波动溢出”效应假说的检验。对此,我们采用针对矩阵元素的似然比检验(LR检验)。原假设为:β21=0,α21=0,即假定通货膨胀率的条件方差仅受自身过去ARCH项和GARCH项的影响,而不受货币增长不确定性的溢出效应影响。这样,就可以构造如下似然比统计量进行“波动溢出”效应检验:

其中:l r和lu分别表示受限制和未受限制下的对数似然值。模型估计与检验的程序代码来自Sheppard提供的估计多元GARCH工具箱。

四、模型估计结果与假设检验

(一)数据与统计描述。样本区间为1983年1月至2008年5月,全部数据来自中国经济信息网数据库。我们采用消费价格指数来反映价格水平的变化。关于货币供应量,则采用狭义货币供应量M 1而非广义货币供应量M2,考虑到月度数据这类高频数据一般存在季节性,我们还进一步利用X-11季节调整方法以剔除季节因素的影响。图1给出了剔除季节因素后的通货膨胀率和货币增长率m1t(环比增长率)的时间路径图。

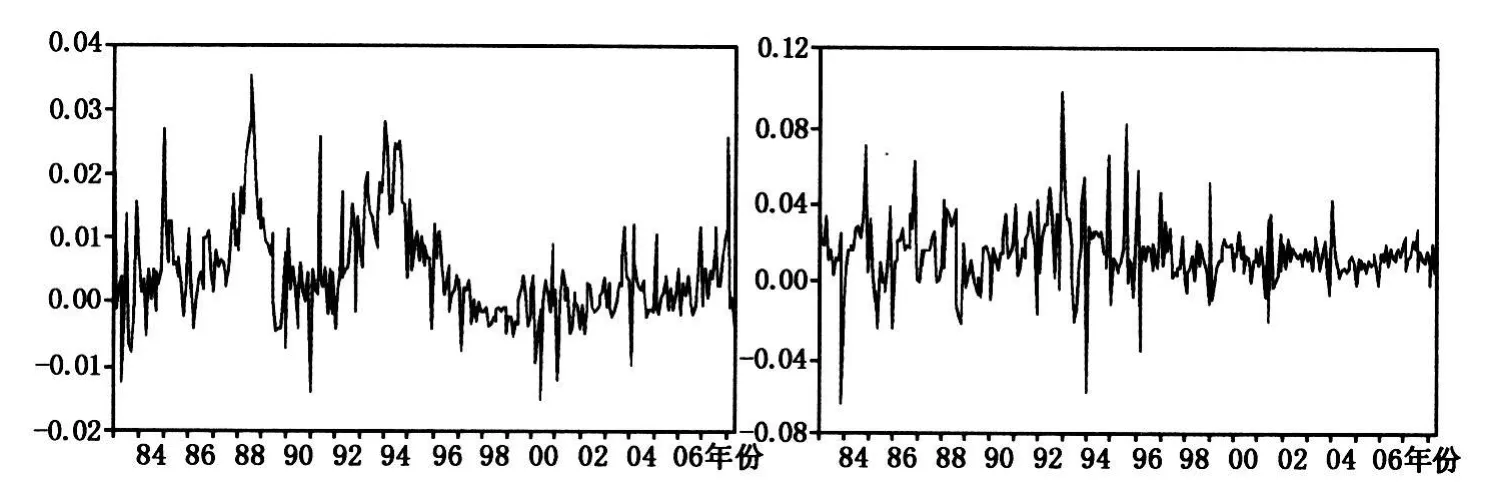
图1 通货膨胀率(左)与货币增长率(右)时间路径图

表1列出了两个时间序列的主要统计特征。表中显示,货币增长率和通货膨胀率的峰度都远大于3,即相对于正态分布两者都出现显著的厚尾特征。平方序列的自相关系数ρ2值以及Ljung-Box Q2(6)统计量都在1%置信水平上显著,表明两者存在明显的ARCH效应,有必要引入ARCH模型来刻画这种时变方差特征。另外,我们对货币增长率和通货膨胀率序列进行了平稳性检验,对于前者,由AIC准则确定的最优滞后阶数为2并包含截距项的条件下,ADF统计量值为-8.307,而5%的临界值为-2.871,因此在5%水平下拒绝货币增长率序列存在一个单位根的原假设。同样对通货膨胀率序列进行ADF检验,在阶数为5并包含截距项的条件下,ADF统计量值为-3.004,小于5%的临界值-2.871,在5%水平下拒绝通货膨胀不确定性序列存在一个单位根的原假设。因此,可以认为在5%水平下货币增长率和通货膨胀率序列都是I(0)过程,可以进行BEKK-GARCH建模。

表1 样本基本统计特征(1983.01-2008.05)

(二)估计与检验结果。一个完整的BEKK-GARCH模型应包括均值方程与方差方程。对于均值方程,我们采用向量自回归模型(VAR模型)进行拟合。VAR模型最优滞后期由AIC准则确定,最大滞后期设为12,经过逐次比较,最终确认VAR(5)最为合适。

表2给出了模型的估计结果,为了简化表格,我们没有给出均值方程系数估计值与方差方程中的常数项系数估计值。

表2第二列是不对参数施加任何约束的BEKK模型估计结果。从估计结果看,在无约束模型的设定形式下矩阵和的对角线元素均在1%水平上显著,这表明对于通货膨胀率和货币增长率,其波动都存在着明显的持续性和聚类性,或者说存在ARCH效应,这与前面表1中的有关结果一致。分别单独对货币增长率和通货膨胀率估计单变量GARCH(1,1)时的对数似然值分别为-1 118.51、-1 490.95,BEKK模型的似然值为-2 576.5,它高于两个单变量模型的似然值之和,可见我们在一个向量的框架内估计两者之间的波动溢出关系确实提高了估计的精度。

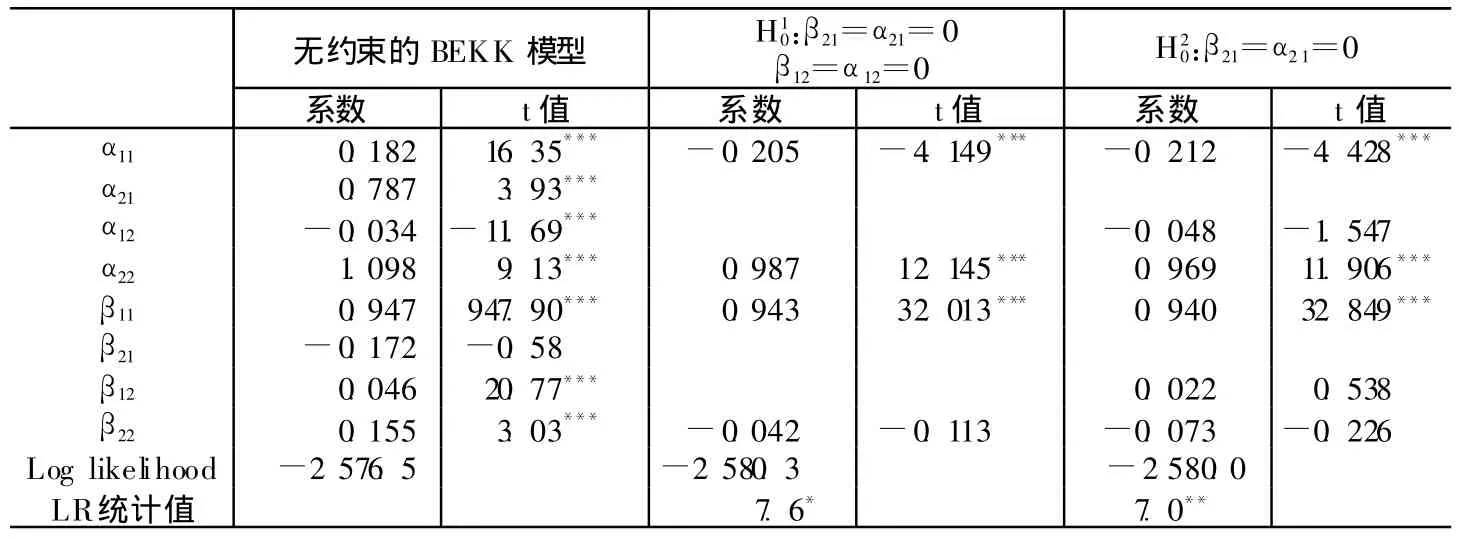
表2 二维向量BEKK-GARCH(1,1)模型参数最大似然估计结果

如前所述,A、B矩阵为对角矩阵的假定,表明每个时间序列的条件方差仅依赖于该时间序列的条件方差自身过去值,而不直接受对方过去波动的影响。相对于非对角矩阵,如果对角矩阵的似然值没有明显下降,则可以认为两个时间序列之间不存在波动溢出,这就是似然比检验的基本思想。类似地,如果仅有原假定:β21=α21=0成立,我们认为不存在货币增长率向通货膨胀率的单向溢出效应。为得到比较稳健的检验结果,我们先对假设:β21=α21=0；β12=α12=0进行检验,即检验不存在任何方向的波动溢出效应,LR统计量服从自由度为4的卡方分布。检验结果见表2第3栏。通过与无约束的BEKK模型的估计结果比较,系数的显著性差别不大,不过加入约束条件后,似然值有了显著下降,LR检验的结果也显示,LR统计量在10%水平上显著,即拒绝了原假设,表明限定不存在任何一个方向的波动溢出效应是一个过强的假设。进一步,在原假设:β21=α21=0条件下重新估计模型,估计结果列在表2中第4栏。我们发现,施加约束条件后,模型的似然值也有了一定程度的下降,LR检验结果显示,在5%水平上拒绝原假设,即表明存在货币增长不确定性显著向通货膨胀不确定性的“波动溢出”效应。

为保证上述模型的正确性,我们还必须对模型的残差进行必要的检验。检验结果显示:三个序列1-5阶的自相关系数在10%水平下均不显著,两个不同滞后期的Q统计量也均不显著,说明这时三个序列已不再存在自相关现象,ARCH-LM(1)检验结果也显示,已不再有ARCH效应,这表明经过该模型滤波后的残差已不再含有能够用于有效预测波动的信息。这意味着形式如式(1)的向量模型将滞后期设定为(1,1)对于描述货币增长率与通货膨胀率的波动性以及两个序列波动的相关性是充分的。

(三)结果分析。根据表2中第二列BEKK模型的系数估计值,由式(2)与式(3),可求得两个序列的条件方差,即为通货膨胀不确定性与货币增长不确定性序列。图2与图3分别给出了通货膨胀不确定性与货币增长不确定性的时间序列轨迹。

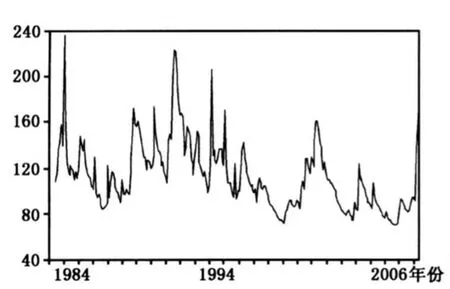
图2 通货膨胀不确定性

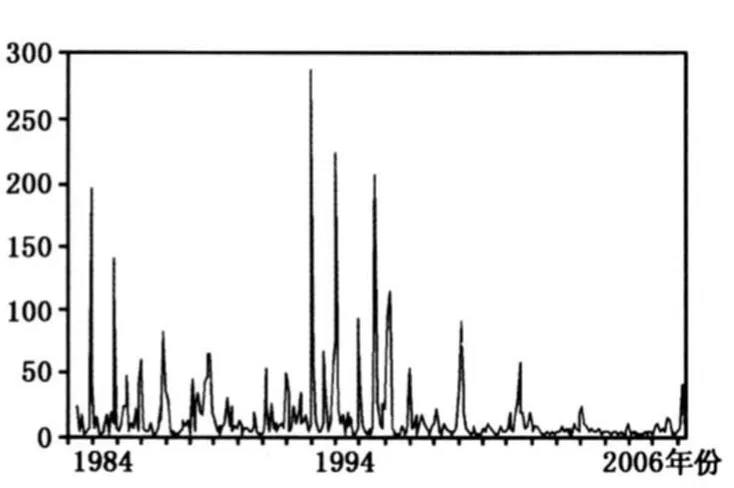
图3 货币增长不确定性

图2与图3反映出两个特点:第一,中国经济在1996年实现“软着陆”前,货币增长不确定性与通货膨胀不确定性时间序列呈现出类似的动态特征。即在1996年之前,货币增长不确定性与通货膨胀不确定性出现峰值次数较为频繁,而之后两者都处于较为平稳的状态。第二,货币增长不确定性在经济实现“软着陆”后,出现峰值次数较之通货膨胀不确定性更少。这表明这个阶段实行的稳健货币政策可能使货币政策工具发挥了对不确定性冲击的吸收和缓冲作用。货币增长不确定性与通货膨胀不确定性上述两个特征与中国应用货币政策干预宏观经济的实践进程是相符合的。1997年以前正是我国货币政策调控机制和宏观经济发生相对剧烈频繁变化时期,这种激烈的变化导致公众通货膨胀预期更加不稳定,通货膨胀预期处于高不确定性状态。1998年以来,中央银行逐步建立起以基础货币为操作目标、货币供应量为中介目标的货币政策调控机制,货币政策整体上保持一种相对稳健态势,且宏观经济的内在稳定性得到明显增强,从而确保了我国货币增长长期处于一种低不确定性的稳定状态。但由于其间出现了诸如1997年亚洲金融危机的各种外部冲击以及2004年初为治理经济过热货币政策发生了明显转变,也导致货币增长出现了短暂的高不确定性。而反观这阶段的通货膨胀不确定性,与1997年之前相比,不但出现峰值较少,而且大部分时间处于低不确定状态。值得注意的是,2008年一季度以来,通货膨胀不确定性突然出现了较大的峰值,反映出公众对未来价格预期的极度不稳定性,而同期货币增长不确定性继续保持在较低状态,这表明2008年以来公众预期的不确定性主要来源于国际石油等大宗商品价格上涨等非货币因素的冲击,这一点应该引起货币当局的关注与重视。货币增长不确定性与通货膨胀不确定性在两个阶段出现的这种正向关联性一定程度上支持了我们所提出的货币增长不确定性向通货膨胀不确定性的溢出效应假说。

正如前面所指出,通货膨胀率的ARCH模型可以度量通货膨胀不确定性,那么为了证实1996年后一系列的货币政策系统性改进是否显著地降低了通货膨胀不确定性的长期成分,可以在成分ARCH模型(Component ARCH)的长期成分方程中加入虚拟变量dummy,从而可以检验虚拟变量对通货膨胀不确定性长期成分影响是正向或者负向。如果dummy系数为负,那么表明虚拟变量引入,确实降低了通货膨胀不确定性长期成分。虚拟变量dummy的具体取值为:1996年之前dummy取值为0,1996年之后取值为1。模型设计如下:

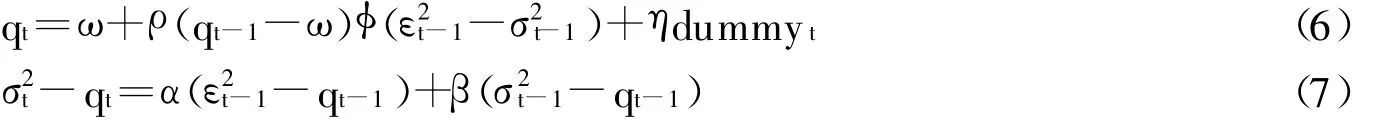
其中:第一个方程与第二个方程分别是长期成分方程与短期成分方程,最终估计结果见表4。

表4 成分ARCH模型估计结果

从模型估计结果看,虚拟变量dummy的估计系数η=-0.0003,在5%水平下显著,这表明1996年以后中央银行一系列货币政策系统性改进确实一定程度上降低了通货膨胀不确定性的长期成分。货币增长不确定性与通货膨胀不确定性自1996年后保持较低水平,得益于以下两个方面的货币政策系统性改进措施:

首先,货币政策目标从不明确转向以稳定币值为首要目标。1996年以前中国货币政策当局的政策目标是双重的,既要稳定币值,又要发展经济。货币政策目标的多重性,导致了货币当局政策的随意性。公众不知道货币政策的确切目标,不清楚中央银行的行动策略,中央银行本身成为一种不确定性的源头,加重了公众通货膨胀预期的紊乱。1995年《中国人民银行法》颁布后,稳定币值成为货币政策的首要目标,这蕴涵了中央银行偏好中稳定通货膨胀的权重增加,这种变化也逐渐为公众所认识。加之随着中国货币政策透明度的不断提高,货币增长不确定性明显下降,产出波动和通货膨胀波动显著下降。

其次,中央银行信誉度、货币政策透明度逐步提高。20世纪80年代以来,中央银行在货币政策执行中,不断通过媒体或其他正式渠道向公众传达政策意图,从而在很大程度上影响了政策的最终效果,尤其自2001年开始,中国人民银行通过多种形式及时地披露货币政策信息,如公布货币政策会议备忘录,发布《中国货币政策执行报告》,深入分析宏观经济金融形势,阐释货币政策操作规则,并披露下一步货币政策取向,这些措施为公众了解央行的政策意图和判断未来政策走势提供了重要依据,央行也在这些系统性措施的改进下提升了自身的透明度和信誉度。

五、结论与政策启示

对于通货膨胀——通货膨胀不确定性关系,大多数文献一般从货币政策当局行为的不可预测性与货币增长对价格水平影响作用的不确定性等角度进行理论阐释。本文并没有沿着这一思路继续从理论上或者实证角度去研究两者的关系,而是归纳这些理论文献,发现一个实证研究所忽略的计量检验内涵,由此提出了一个计量检验假说,并运用多元GARCH模型,利用中国数据对假说进行了实证检验。结果发现,存在货币增长不确定性显著向通货膨胀不确定性“波动溢出”的效应。假说命题与实证检验结果的政策含义非常清楚:降低货币增长不确定性是稳定与引导公众通货膨胀合理预期进而降低通货膨胀不确定性的重要途径。我国20世纪90年代中期以后实行稳健的货币政策期间,货币增长不确定性与通货膨胀不确定性显著降低的事实就支持了这个观点。而在这之前,由于其政策目标变化大以及透明度、信誉度不高等方面的原因,货币政策工具并没有发挥出对不确定性冲击的吸收和缓冲作用,公众面临的不确定性大,导致呈现出货币增长不确定性与通货膨胀不确定性正向关联的特征,即所谓的“波动溢出”效应。

当前我国虽然还不存在通货膨胀问题,但因实行经济刺激计划,已使国内投资大幅增长、信贷规模创出历史天量；加上国际上美元贬值预期和初级产品、农产品价格上涨,促使通胀预期重新抬头。对此,决策层对通胀预期保持着高度警惕,已把管理通胀预期与保增长、调结构相提并论,这表明管理通胀预期已被纳入今后政策调控范围。结合本文研究结论,我们建议通胀预期管理应着眼于短期和长期。从短期看,为使市场能够形成稳定的政策预期以致稳定的通胀预期,中央银行当前应设定一个清晰的信贷增长目标和货币供应量目标。目标的设立可以避免金融机构为防止可能的信贷紧缩而大规模提前放贷,从而防止信贷分布的不均衡现象,降低货币增长不确定性。同时以微调、局部调整为主,尽力避免经济刺激方案过度频繁调整,避免公众对政策预期的不确定性现象,从长远看,货币增长不确定性的下降实质上是货币当局信誉程度、货币政策透明度等货币政策系统性改进的漫长过程,在这方面,我国中央银行可以借鉴通货膨胀目标框架的优点,逐步完善货币政策制度。

[1]胡日东,苏梽芳.中国通货膨胀与通货膨胀不确定性的非线性关系[J].数量经济技术经济研究,2008,(2):28-37.

[2]贾俊雪.中国货币增长的不确定性及其对宏观经济的影响[J].中国软科学,2006,(11):22-30.

[3]徐亚平.货币政策有效性与货币政策透明制度的兴起[J].经济研究,2006,(8):26-36.

[4]赵留彦,王一鸣.A、B股之间的信息流动与波动溢出[J].金融研究,2003,(10):41-56.

[5]Ball L.Why does high inf lation raise inflation uncertainty？[R].Working Paper No.3224,1990,National Bureau of Economic Research.

[6]Dennis,Powers.Stochastic money demand and the inf lation-uncertainty relationship[J].The Manchester School Supplement,1997,(25):59-68.

[7]Holland S.Uncertain effects of money and the link between the inflation rate and inflation uncertainty[J].Economic Inquiry,1993,(1):39-51.

[8]Kim,Chang-Jin,et al.Sources of monetary growth uncertainty and economic activity:The time-varying-parameter model with heteroskedastic disturbances[J].The Review of Economics and Statistics,1993,(3):483-492.

[9]Sylvester C W Eijffinger.Why money talks and wealth whispers:Monetary uncertainty and mystique[J].Journal of Money,Credit,and Banking,2000,(2):218-235.