集值映射空间上可数强Fan Tightness

郭先一，李祖泉

(杭州师范大学 理学院，浙江 杭州 310036)

1 引言及预备知识

在此，拓扑空间X,Y均是完全正则T1的，M(X,Y)为拓扑空间X到Y上的所有集值映射族，K(X)表示X的所有非空紧子集族，N表示自然数集，R表示实直线，0是可数基数，λ为任意无限基数，文中未定义的术语和符号均以文[4-5]为准.

设f∈M(X,Y)，对A⊂X，记f(A)=∪x∈Af(x)；对B⊂Y，记

f+(B)={x∈X:f(x)⊂B};f-(B)={x∈X:f(x)∩B≠∅}.

对于X的子集K，Y的子集U，V，记

W+[K,U]={f∈M(X,Y):f(x)⊂U,x∈K};W-[K,V]={f∈M(X,Y):f(x)∩V≠∅,x∈K}.

以所有形如W+[K,U]，W-[K,V]的集为子基生成M(X,Y)的拓扑Tk称为紧开拓扑，其中K为X的紧子集，U，V为Y的开子集[6].

记Ck(X,R)为X到R上的所有点紧致的连续集值映射族，并且赋予紧开拓扑，Ck(X,R)简记为Ck(X).

2 主要结果

空间X的tightness定义为t(X)=sup{t(X,x):x∈X}，其中X在x的tightness定义为t(X,x)=0+min{λ:对于X的子集Y，若则存在Y的子集Z，使得|Z|≤λ且}.

空间X的fan tightness定义为ft(X)=sup{ft(X,x):x∈X}，其中X在x的fan tightness定义为ft(X,x)=0+min{λ:对于X的子集列{An}和存在An的子集Bn，使得|Bn|≤λ且}.

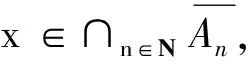
易见，第一可数空间⟹可数强fan tightness⟹可数fan tightness空间⟹可数tightness空间.

空间X的子集族U称为X的k覆盖[3]，若对于每一个紧子集K⊂X，存在U∈U，使得K⊂U.若集族U由空间X的开子集组成，则U称为X的开k覆盖.

定义2对于任意非空A,B⊂R，定义

ρ(x,A)=inf{|x-y|:y∈A}，

ρ(A,B)=sup{ρ(x,B):x∈A}，

d(A,B)=sup{ρ(A,B),ρ(B,A)}，

对于x∈R，记d(x,A)=d({x},A).

定义3设ψ是拓扑空间族，令∏Yα∈ψYα是空间族ψ的Tychonoff积拓扑，对于每一个Yα∈ψ，令pYα:∏Yα∈ψYα→Yα是投影映射.若X是拓扑空间，定义集值拓扑积映射T:M(X,∏Yα∈ψYα)→∏Yα∈ψM(X,Yα)为：对于每一个f∈M(X,∏Yα∈ψYα)和Yα∈ψ，有pM(X,Yα)∘T(f)=pYα(f).

引理1[5]设ψ是拓扑空间族，X是拓扑空间，则集值拓扑积映射T:Ck(X,∏Yα∈ψYα)→∏Yα∈ψCk(X,Yα)为同胚映射.

定理1对于空间X，下列条件是等价的：

1)sft(Ck(X))=0;

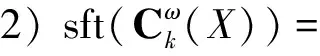
3) 对于X的每一个开k覆盖列{Un}n∈N，都存在Un∈Un，使得{Un}n∈N是X的开k覆盖.

证明1)⟹3) 设{Un}n∈N是空间X的开k覆盖列，对于每一个n∈N，令

An={f∈Ck(X):存在U∈Un，使得f(X-U)⊂{0}}.

下面证明An是Ck(X)的稠密子集.设

为Ck(X)的基中的开集，其中K∈K(X)，V1,V2,…,Vk为R中的开集.因为Un是X的开k覆盖，存在U∈Un，使得K⊂U.设f∈W[K,V1,V2,…,Vk]，则

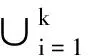
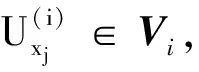
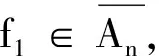
〈UΔ〉={K∈H(R):K⊂∪UΔ,K∩U≠∅,U∈UΔ}

形式.这样乘积空间Rω上的紧子集超空间(H(R))ω的基为形如

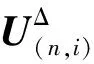
W[A,Vn]={g∈Ck(X,Rω):g(A)∈Vn}，

存在g∈An∩W[A,Vn]，使得A⊂{x:g(x)∈Vn}∈Vn.令M={n∈N:X∈Vn}.若M为无限集，则对于f的任意邻域W[A,〈U1,U2,…,Uk〉]，因为f(A)为紧的，由文献[7]的28.10-28.11可知R是可数型的，从而Rω是可数型的，可设f(A)的局部基VA⊂{Vn:n∈N}是递缩的，而〈U1,U2,…,Uk〉为含f(A)的开集，故存在空间(H(R))ω的基中开集Vm∈VA(m∈M)，使得对于每一个x∈A，有

f(x)∈Vm⊂〈U1,U2,…,Uk〉，

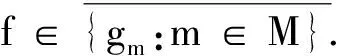
[1] Sakai M. Property C″and function spaces[J]. Proc Amer Math Soc,1988,104:917-919.

[2] Mccoy R A, Ntantu I. Topological properties of spaces of continuous functions(Lecture Notes in Math,No.1315)[M]. Berlin: Springer-Verlag,1988.

[3] 林寿.度量空间与函数空间的拓扑[M].北京:科学出版社，2004.

[4] Engelking. General topology[M]. Warszwa: Polish Scientific Pubilishers,1977.

[5] Li Zuquan. Tightness and fan tightness on multifunction spaces[J]. J Math Res Exposition,2008,28(4):1007-1012.

[6] 张红，杨丽华，李祖泉.集值映射空间的可数性和度量化[J].杭州师范大学学报:自然科学版,2009,8(3):180-183.

[7] 儿玉之宏，永见启应.拓扑空间论[M].北京:科学出版社，2004:152-153.