基于二次相关的时延估计方法研究＊

杜 娟，程 擂

（中北大学电子测试技术国家重点实验室，太原 030051）

0 引言

声被动定位是一种利用目标音频信号来实现定位的无源探测技术，具有显著的优越性［1］。声被动定位系统采用被动工作方式，具有隐蔽性好、不受视线和能见度的限制、不易被干扰、低功耗和低成本的优点［2］。

在对目标信号进行定位和探测、识别和跟踪时，时延估计精度直接影响到定位结果。根据不同的要求，时延估计有不同的方法，主要包括相关估计法、参数估计法、高阶统计法等。其中以互相关法和相位谱法算法简单、计算量小、易于实现而得到了广泛应用。然而，互相关时延估计法分辨率与信号带宽近似成反比，因此很难估计多目标时延。而相位谱时延估计只能估计单目标时延，并且存在相位解绕问题［3］。基于此，文中提出了一种基于传感器网络被动声定位的二次相关时延估计方法，探讨了该方法的估计精度问题，结果表明该方法相对于一次相关可以较为准确的进行时延估计，进而实现声源探测及定位。

1 空间任意多元传感器阵列模型

在被动定位和实际应用中，空间任意多元阵列［4］相对于平面多元阵列更普遍、更广泛的应用。文中以空间任意多元传感器阵列为模型来研究时延估计方法。任意多元传感器阵列模型如图1所示。

图1 定位原理图

假定在空间同一坐标系下任意布放N元传感器阵列（p1，p2，…，pn），其空间相对位置已知。假定声源在介质中的传播速度已知。根据各个传感器位置坐标，可以得到（n－1）组定位方程：

其中：

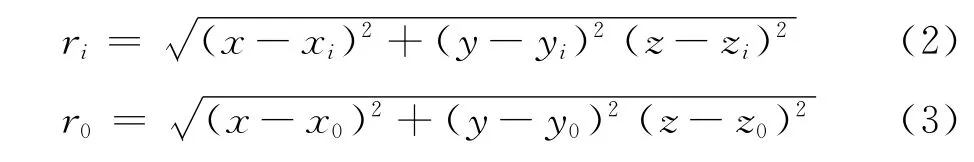
上式中，ri、r0、r0i和t0i分别为第i号传感器距离声源的距离、参考传感器距离声源的距离、两者之间的距离差以及时间差，c为声音在介质中的传播速度。

从上式可以看出，只要已知传感器的位置坐标（xi，yi，zi）和不同传感器接收到信源信号的时延t0i，即可通过求解上式（1）中（n－1）组定位方程得到声源的空间位置（x，y，z）。

2 相关算法求时延

一次相关［5］在作时延估计时，由于受噪声影响较大，存在着估计精度不高的问题。二次相关法首先将信号作自相关提高信噪比，再将自相关函数同互相关函数作相关得到时延值。

假定：

1）信源为窄带信号；

2）噪声为高斯白噪声；

3）同一传感器接收的信号与噪声、不同传感器接收的噪声与噪声互不相关。

2.1 一次相关

假定信号模型为：

信号x1（t）的自相关函数可以表示为：

根据上述假设，得到：

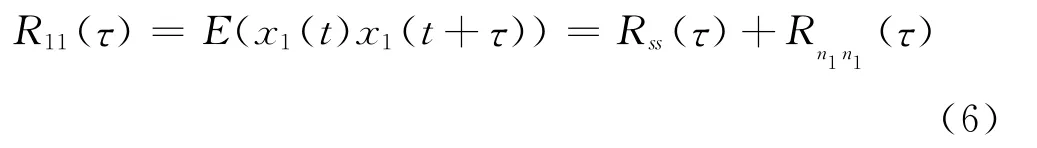
其中，Rn1n1（τ）是τ＝0的冲击函数。

可以看出，一次自相关提高了信号的信噪比。

2.2 二次相关

将自相关函数和两路信号的互相关函数作相关，即：

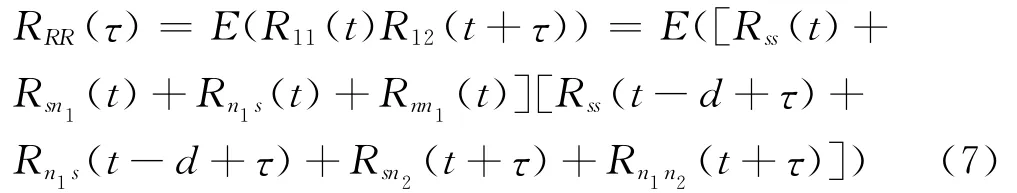
同样根据上述假设，可以得到：

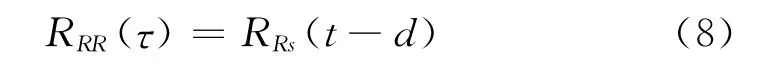
相关函数最大值点对应的横坐标就是时延。

相对于一次相关估计，二次相关法时延估计方法减小了噪声对信号的影响，可以在更低的信噪比下进行时延估计，使用范围更加的广泛。

3 实验验证

实验是在室内环境下完成的。以标准正弦信号为声源，采样频率为500k Hz，室温下声速为：c＝340 m／s。

3.1 时延理论值

传感器布阵采用随机布阵方式，布阵空间为三维空间。传感器个数为6个。以1号传感器为基准，分别计算得到2～6号传感器与1号传感器距离声源的距离差，以声速c＝340 m／s计算得到时延理论值，如表1所示

表1 时延理论值

3.2 时延实验值

3.2.1 一次互相关时延估计

将传感器1与传感器2接收到的信号直接作互相关（见图2）。

图2 一次互相关时延估计

一次相关函数最大峰值所对应的时间点即为时延。计算得到时延为5.1801 ms，距离差为：1.7612 m；

3.2.2 二次互相关时延估计

将传感器1接收到的信号先作自相关，再将传感器1和传感器2接收到的信号作互相关，最后将自相关函数同互相关函数作相关（见图3）。

图3 二次相关时延估计

二次相关函数最大峰值所对应的时间点即为时延。计算得到时延为4.9405 ms，距离差为：1.6798 m。

3.2.3 实验值同理论值比较

重复上述步骤，得到3～6号传感器的时延值。将理论值与实验值对比，如表2所示（表中A、B分别表示用一次相关法和二次相关法计算）。

其中，RE表示时延估计相对误差，即：

从表2中可以得出：用一次相关法作时延估计时估计误差较大，平均估计误差为REA＝2.6955%。用二次相关法作时延估计时估计误差明显减小，平均估计误差为REB＝1.2702%。

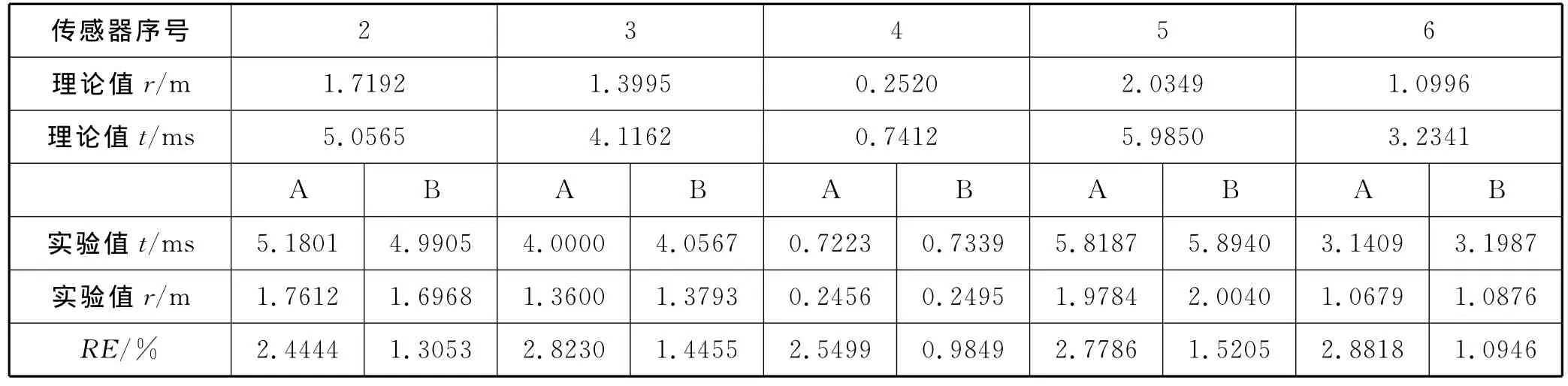
表2 理论值与实验值对比

4 结论

室内环境下，在被动定位算法的基础上，以空间任意多元传感器阵列为模型，以标准的正弦信号为声源，对一次相关时延估计法和二次相关时延估计法进行了研究。理论结果表明：二次相关法作时延估计时能够降低噪声对信号的影响，提高时延估计精度。实验结果也表明：在对空间任意多元传感器阵列进行时延估计时，二次相关法的平均时延估计精度可以达到1.2702%，相对于一次相关方法在对时延进行估计时明显的提高了估计精度。

［1］ 毕延文.基于时差法的飞行器声被动定位技术研究［D］.西安：西安电子科技大学，2005.

［2］ 庞学亮，张效民.基于二次相关水下声源定向（时延）研究［J］.探测与控制学报，2005，27（3）：41－43.

［3］ 行鸿彦，唐娟.时延估计方法的分析［J］.声学技术，2008，27（1）：110－114.

［4］ 王文川，韩焱.空间任意声阵列无源定位研究［J］.海洋技术，2009，28（2）：62－64.

［5］ 唐娟，行鸿彦.基于二次相关的时延估计方法［J］.计算机工程，2007，33（21）：265－267.