分层弹底径向分离速度测试研究＊

田 铭，陈西峰，刘文举，吴 卉

（中国兵器工业第203研究所，西安 710065）

0 引言

国内在研某型号炮射末敏弹采用分层弹底径向分离方案以达到抛撒分离阶段防碰撞的目的，而弹底径向分离速度是评价弹底径向分离效果好坏的重要标志。在实际测试中，分层弹底径向分离速度的测试精度对分层弹底径向分离数学模型的验证及修正有着极其重要的影响。

文中主要基于低伸弹道抛射试验，通过模拟实际抛撒分离阶段分层弹底的分离过程，提出一种全新的简单有效的测试方案，并针对该方案中所测试的数据进行误差分析，将误差减小到合理范围，以保证试验数据的精度及合理性。

1 径向速度的测试

1.1 测试方案

如图1所示，采用在弹道线两侧放置两台相互正交的高速摄像机，摄像机各成α、β角放置，选择摄像机对焦点应在理论弹道线上，且能保证理论分离点在摄像机视场以内。

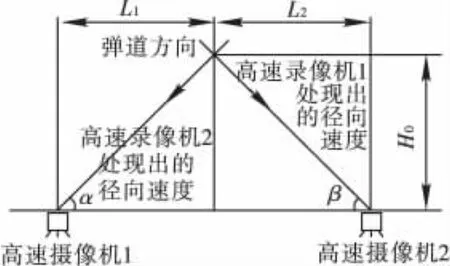
图1 高速摄像机在靶板附近放置位置图

1.2 径向速度的合成

如图2所示，通过对两台高速摄像图像处理，得到弹底径向分离速度在每个摄像投影面上的分量，通过计算可得到分层弹底的径向分离速度。

设弹底实际分离速度为V0，v1为高速摄像机1处理出的弹底分离速度，v2为高速摄像机2处理出的弹底分离速度，则：

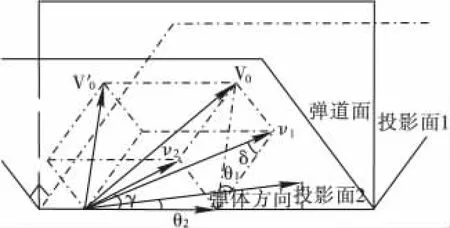
图2 高速摄像处理出的径向速度合成示意图

其中：δ为v1与投影面1垂直方向的夹角，γ为v2与投影面2水平方向的夹角。

由图2可知，V0是通过运算合成出的弹底实际分离速度，但这并不是弹底实际径向分离速度。

分析可知，先将运算合成V0所在坐标系（以下称为弹底速度坐标系）绕X轴方向逆时针旋转45°－θ1（因为投影面与弹道面夹角为45°），再将坐标系绕Z轴逆时针旋转θ2，即可得到以弹体实际方向为X轴的弹体坐标系（以下称为弹体坐标系）。

转换矩阵分别为：

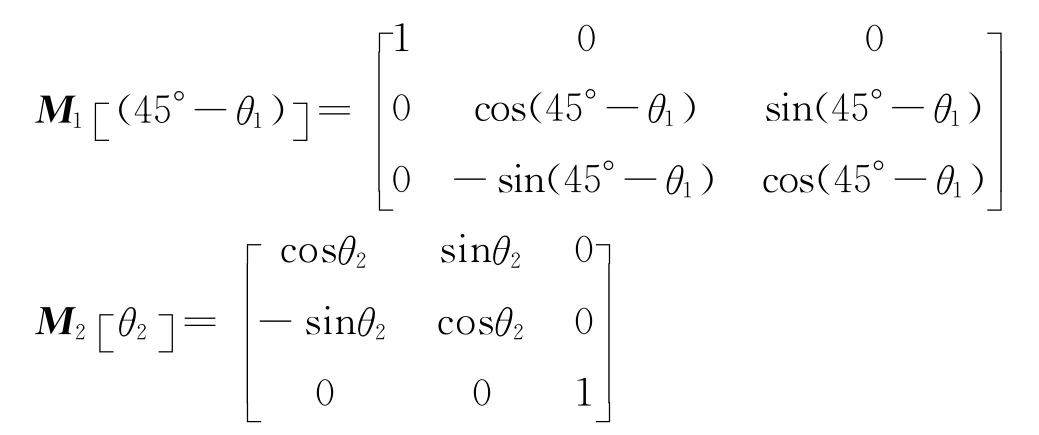
而σ1、σ2分别为在两个投影面上的弹体与屏幕水平方向夹角，若假设两投影面正交且夹角相等，则理论上σ1＝σ2，即

在弹底速度坐标系内，实际弹底分离速度V0＝通过2次坐标转换到弹体坐标系下：

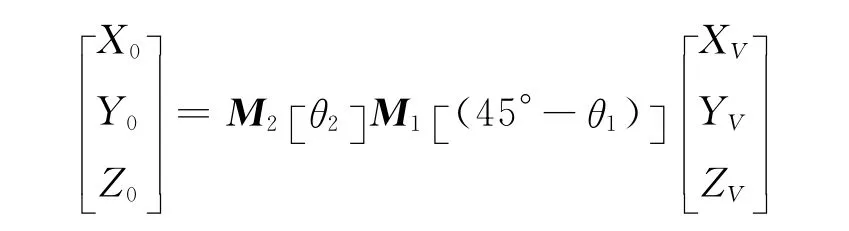
方程右侧所需数据均可由高速录像图像分析处理得出，即得到实际径向分离速度V′0。

2 误差分析

在实际操作中，不可避免的会有各类误差，因此，必须分析各类误差对整个运算结果的影响。

2.1 速度计算误差

速度计算误差主要由两部分组成，一是由二维图像获取三维信息时产生的误差，二是画面分辨率误差。

2.1.1 由图像获取产生的误差

根据图像分析处理速度的原理，在高速录像图像上，截取一定时间段内同一观测物的运动轨迹，除以相应时间，即为单位时间内运动的距离，也就是所处理出的速度，此速度为实际速度在摄像机所拍摄平面内的投影，根据摄像机与目标所成的角度进行相应的换算，最终得到所需要的实际速度。

但是，观测物在视场内运动，必将导致观测物偏离视场中心线（包括水平跟垂直两条中心线），根据光学成像原理，此时在屏幕中截取的运动轨迹，距离并不是实际距离，如图3所示，即r3≠s2－s1，因此根据图像处理出的速度就将出现误差。

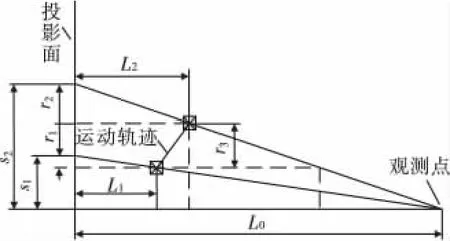
图3 摄像机成像分析

其中L0为高速摄像机距投影面距离，L1、L2为观测物径向偏离投影面的距离，s1、s2均为观测物在录像画面中偏离屏幕中心线（竖直方向）距离，r3为观测物运动轨迹投影尺寸，由图可知，实际观测物在录像画面中的成像尺寸为s2－s1，则测量误差为Δh＝又即可得到×100% ，其中，L0已知，s1、s2可在录像屏幕上测出，因此误差大小与L1、L2有关。

通过计算可知本方案中此误差在6%以内。

2.1.2 由图像分辨率产生的误差

图像分辨率误差主要由图像画面分辨率及视场大小决定，比如视场范围2 m×2 m，分辨率为1024×1024，即屏幕上单位像素点可表示约2 mm实际距离。视场范围越小，单位像素代表的实际距离越小，单位像素代表的实际距离即是测试误差，而本方案中考虑弹底径向分离距离在50～100 mm，因此由画面分辨率引起的误差应该在2%～4%之间。

2.2 角度误差

角度误差包括两类，一是摄像机拍摄角度的误差，因为实际地理地貌、弹道线本身存在高度误差及摄像机三脚架高度限制等原因产生的误差；二是弹道偏置的误差，即为偏流角引起的误差。

2.2.1 第一类角度误差

第一类角度误差，主要集中在两个问题上，第一，拍摄高度问题；第二，拍摄角度问题。

拍摄高度导致的误差分析：

若将高度误差控制在0.1 m以内，分离点在视场内，径向分离范围在0.2 m×0.2 m以内，拍摄位置距弹道线铅垂面距离3 m，则因为高度偏差造成的误差在0.5%内。

拍摄角度导致的误差分析：

若将拍摄角度误差控制在1°以内，其他条件同上，则由于拍摄角度误差所引起的误差在0.1%内。

由此，第一类角度误差根据实际测试情况可以控制在2%以内。

2.2.2 第二类角度误差

第二类角度误差，主要是由于偏流角引起的，在实际测试中，可先试射一发沙榴弹用以修正偏流角对实际拍摄时的影响，即将炮口角度反向偏置偏流角度（或偏移两台摄像机的布置位置），使得实际弹道修正至理论弹道线上，可以尽量减少偏流角φ对测试数据的影响。

在本次试验中，由于射角较小，因此实际偏流角也较小，通过上述办法修正后对实际数据的影响可以忽略。

2.3 方案可行性

通过对误差的分析修正（如补偿法），理论上可以将测试误差控制在5%以内，因此，可以认为试验数据能够满足试验目的，可以给予理论模型提供有效的试验支持。

3 结论

本方案得到弹底径向分离速度的精度较高，对试验条件的要求较低，方法简单，通过对物体成像原理的深入研究分析，可以更大化的提高精度，降低测试误差，给予建立分层弹底径向分离数学模型提供了有力的试验依据，对理论模型的修正起着指导性的作用。

［1］ 刘文举.炮射末敏弹后抛式子弹抛撒分离技术研究［D］.北京：北京理工大学，2000.

［2］ 朱新宏，张永生.某武器外弹道飞行姿态测试方法探讨［J］.测试技术学报，1998，12（3）：120－124.

［3］ 杨新军，吴华夏，余晓芬，等.机载护目镜型头盔显示器畸变校正［J］.光子学报，2010，39（3）：455－458.

［4］ 潘国荣，赵鹏飞.基于空间向量的三维基准转换模型［J］.大地测量与地球动力学，2009，29（6）：79－82.

［5］ 王军德.径向畸变摄像机的标定［J］.科技信息，2009（25）：465－466.