适用于高旋弹药的MI MU角速率解算算法研究＊

王 博，李 杰，于希宁，杜 英

（中北大学电子测试技术国家重点实验室，太原 030051）

0 引言

对于常规高速旋转弹药来说，其工作时间较短，但沿弹体轴向的转速较高，一般转速要达到20r／s，甚至更高；发射时炮弹在火药气体作用下高速运动，弹体轴向加速度高达几百到上万g。此外，弹体上空间有限，要求测试传感器具有体积小、功耗低、重量轻的特点。对于微惯性测量组合而言，国内获取抗高过载环境下的高精度大量程陀螺十分困难，因此常规有陀螺捷联惯性测量系统难以满足高速旋转弹药制导化应用为背景的测试需求［1］。随着加速度计器件性能提高，利用加速度计实现载体角速率测量成为惯性测量技术发展的重要方向，具有良好的应用前景。

当前，无陀螺惯性测量组合解算角速率精度普遍较低，解算误差随时间严重发散，难以满足实际工程应用需求。此外，由于在角速率解算过程中需要引入判断角速率符号的问题，在小角速率和小角加速度情况下，容易出现符号误判［2－3］。为了解决上述问题，文中提出了一种十二加速度计配置方案，通过优化角速率解算算法，在一定程度上提高了角速率解算精度的同时，有效避免了上述问题。

1 十二加速度计配置方案

十二加速计惯性测量组合加速度计配置如图1所示［4－5］，其中加速度计安装位置向量ri，方向向量θi分别为：

固联于载体之上，安装方向向量为θ，安装位置向量为r的加速度计输出比力模型为：

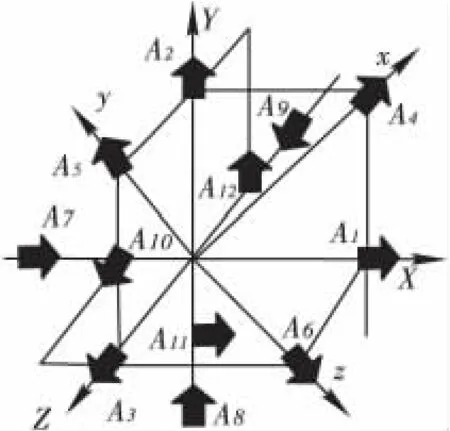
图1 加速度计配置方案

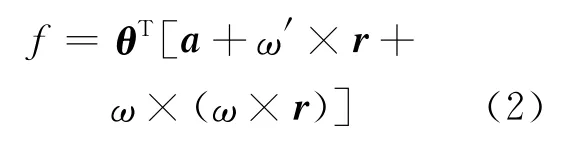
其中：a为加速度计在载体坐标系中的比力分量，ω为载体角速率。利用式（2）可以得到十二个加速度计输出比力方程，并通过该方程直接计算得到角速率平方项，角速率交叉乘积项和角加速度项，即：

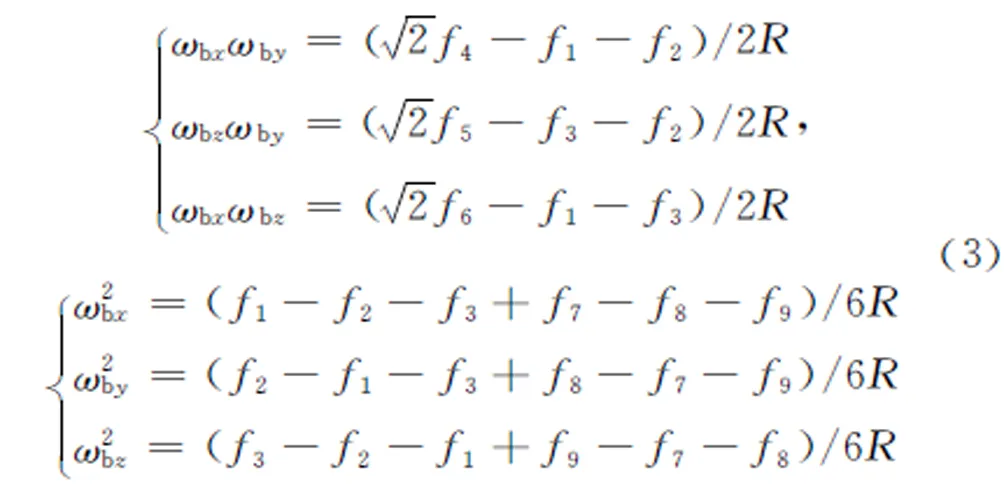
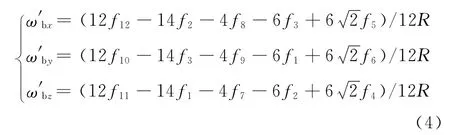
其中：fi表示第i个加速度计输出比力信息，ωbi表示载体坐标系相对惯性坐标系转动角速率在i轴投影，ω′bi表示载体坐标系相对惯性坐标系转动角加速度在i轴投影。

2 角速率解算算法优化

2.1 常见角速率解算算法比较

角加速度积分法是角速率解算最常见的方法。该方法无需再引入角速率符号判断，但不足之处也是十分明显。首先，该方法在计算角速率绝对值过程中引入时间因素，从而导致计算误差随时间迅速积累发散，难以满足较长时间测量需求；其次在角速率符号判断上存在小角速率和小加速度情况下符号误判现象。

角速率绝对值也可以通过角速度平方项开方得到，即直接开方法。由于角速率平方项可以通过加速度计输出直接计算，因此可以较为准确得到角速率绝对值，并且计算误差不随时间积累。角速率交叉乘积项通过变换也可以得到角速率平方项，进而开方得到角速率绝对值，即间接开方法。但该方法缺点是角速率平方项不是直接由加速度计输出计算而来，当变换过程中分母项出现接近零时会将测量误差严重放大，出现一系列不连续的跳跃奇异值点，即过零震荡现象。角速率交叉乘积项也可以通过变换直接计算角速率，该方法优点是将角速率绝对值计算和角速率符号判断融为一体，缺点与间接开方法一样存在过零震荡现象。

除了上述提到的角速率解算解析算法，角速率解算算法还有通过估计角速率解算残余误差补偿角速率解算值的残余误差迭代补偿法和基于构造角速率微分的角速率微分算法。前者的缺陷是补偿后的角速率中包含加速度计常值漂移引起的迭代误差随时间积累分量，从而导致解算角速率随时间积累发散；基于构造角速率微分的角速率微分算法不需要引入角速率符号判断的问题，但其致命的缺陷与间接开放法和角速率交叉乘积项直接计算法一样，存在过零震荡现象。

2.2 角速率组合解算算法

在分析常见角速率解算算法优劣的基础上，文中提出了一种有效的角速率解算组合方法。由于该配置方案是以高速旋转弹药制导化应用为背景提出的，因此在飞行的大部分时间沿轴向角速率很大，利用积分法判断ωbx符号不会出现误判现象。其他轴向角速率通过角速率平方项辅助角速率交叉乘积项获取。即：

此时，ωbx的值由平方项开方得到，而平方项直接由加速度计输出计算获取，因此ωbx的计算精度很高；ωby及ωbz在解算过程中，由于ωbx很大，从而有效避免了过零震动，同时提高了ωby及ωbz解算精度。

3 仿真分析

为了验证上述角速率解算算法的有效性，对其进行了计算机仿真。在不考虑空气阻力等外界因数和安装误差的情况下，设火炮射角45°，射向为零，弹体以初速1000 m／s发射出去，并以固定角速率1000o／s绕弹轴旋转直至落地；惯性测量组合中加速度计测量精度为10－4g，随机白噪声均方根为10－6g，安装半径0.05 m，仿真时间10s，步长为0.001 s。

图2为y轴角速率仿真曲线。从仿真结果可以明显看出，在极短时间内积分法解算载体角速率精度较好，但由于解算误差随时间积累，难以满足较长时间高精度测量需求；直接开方法解算角速率过程中积分法判断角速率符号，存在小角速率和小角加速度情况下角速率符号误判问题，而角速率的绝对值解算误差较小；间接开方法和微分法都存在分母项接近零时明显的过零震荡现象，将测量误差严重放大；残差估计补偿法在角速率解算过程中近似计算引入了时间因素，导致角速率解算随时间积累发射；组合法解算角速率较好解决了上述方法存在的问题。

图3为y轴角速率误差仿真曲线。组合法的角速率解算精度比积分法明显高出一个数量级，而且不随时间积累；比残差估计补偿法提高约100倍。

4 结论

图2 载体坐标系中y轴角速率仿真曲线

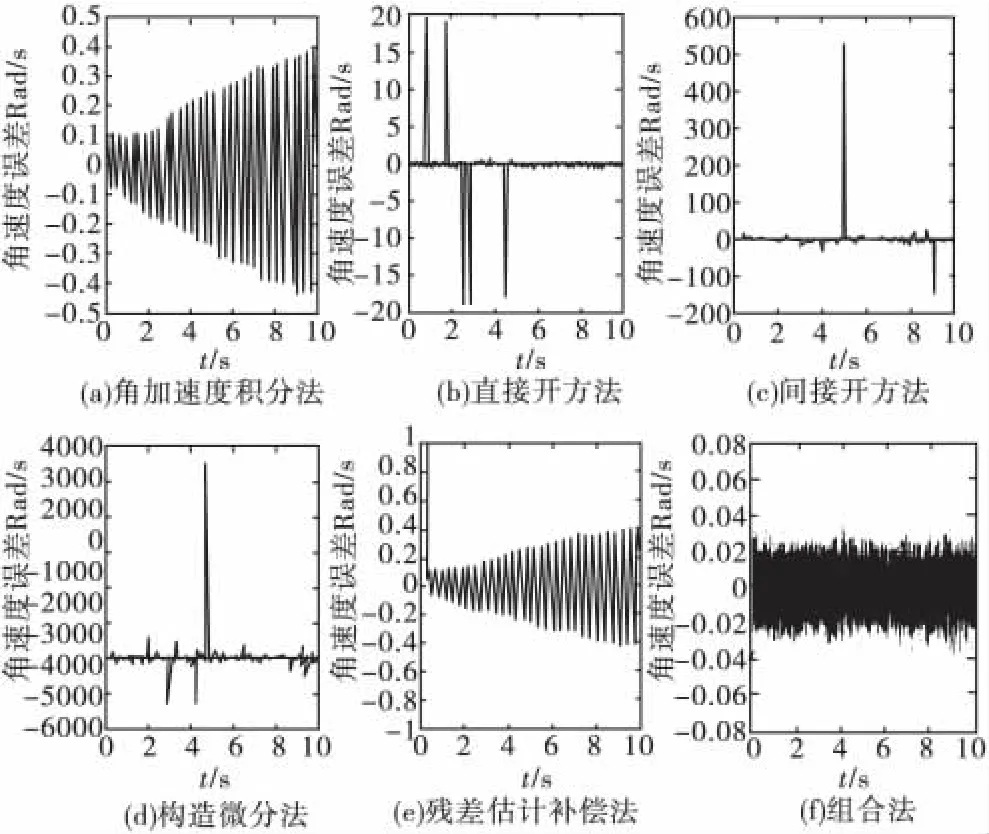
图3 载体坐标系中y轴角速误差仿真曲线

无陀螺捷联惯性测量系统克服了陀螺性能限制引入的困扰，能够满足高速旋转弹药制导化应用中的测试需求。基于上述认识，文中提出了一种适用于高速旋转弹药应用环境的十二加速度计无陀螺惯性测量组合配置方案，并通过几种常见角速率解算算法优劣比较，选择了一种角速率组合解算算法较为准确的解算出载体角速率，从而为下一步载体惯性参数解算减小误差奠定基础。仿真结果表明，基于该方案的角速率解算算法是可行的。值得一提的是由于文中理论推导和仿真对于加速度计的安装误差均采取了理想化处理，实际应用过程中加速度计安装误差不可避免，从而给角速率解算带来严重影响［7－8］。因此，针对该方案的加速度计安装误差补偿将成为下一步研究的重点。

［1］ 牟淑志，卜雄洙，李永新，等.高转速载体惯性测量组合研究［J］.弹道学报，2006，18（4）：85－88.

［2］ 丁明理，王祁.无陀螺惯性测量组合研究现状概述［J］.中国惯性技术学报，2005，13（4）：83－88.

［3］ 赵龙，陈哲.提高无陀螺捷联惯导系统角速度解算精度的新方法［J］.系统仿真学报，2005，15（4）：579－603.

［4］ 覃方君，许江宁，李安，等.一种准无陀螺惯导系统解算新方法研究［J］.系统仿真学报，2008，20（1）：49－52.

［5］ 薛红香，夏全喜，孙明，等.无陀螺惯性测量单元设计及仿真分析［J］.中国惯性技术学报，2008，16（2）：154 －158.

［6］ 郝燕玲，刘志平.无陀螺捷联惯导系统角速度解算新方法［J］.弹箭与制导学报，2009，29（4）：35－38.

［7］ 周百令.一种新型的单陀螺多加速度计捷联惯导系统［J］.中国惯性技术学报，2002，10（1）：6－9.

［8］ 曹咏弘，祖静，林祖森.无陀螺捷联惯导系统综述［J］.测试技术学报，2004，18（3）：269－273.

［9］ 汪小娜，王树宗，朱华兵.无陀螺捷联惯导系统加速度计安装误差研究［J］.兵工学报，2008，29（2）：159－163.