末制导寻的反导导弹脱靶量分析

韩朝超, 黄树彩, 张建伟

(空军工程大学导弹学院,陕西三原713800)

0 引言

反导作战时,反导导弹的末制导主要采用寻的制导方式,要求拦截弹有较小的脱靶量甚至能直接碰撞,即使是最保守的脱靶量也应当小于拦截弹战斗部的杀伤半径[1]。

脱靶量作为末制导能力的衡量指标,对寻的制导导弹的脱靶量产生影响的因素主要有目标机动、闪烁噪声、距离独立噪声和角噪声等[2]。其中:角噪声主要是导引头天线罩误差的影响所致。文献[3]指出典型的导弹制导系统可表述为一个五阶二项式系统。

1 不同因素对脱靶量的影响

1.1 目标机动和有效导航比的影响

对文献[3]的典型导弹制导系统,若不考虑闪烁噪声、距离独立噪声、接收机噪声和导引头天线罩误差的影响时,有效导航比和目标机动对脱靶量的影响结果如下[4]。

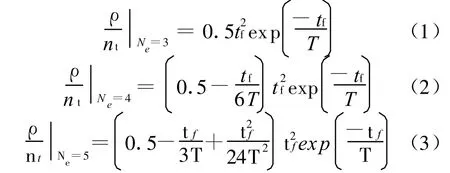
式中:ρ为脱靶量;t f为导弹飞行时间;T为制导系统时间常数;n t为目标机动加速度;N e为比例导引的有效导航比。根据上述表达式,若制导时间常数为0.7,则有效导航比和目标机动对脱靶量的影响如图1和图2所示。

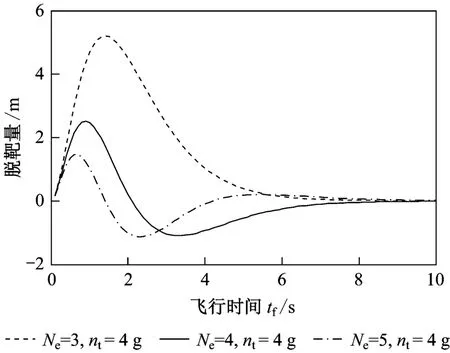
图1 有效导航比对脱靶量的影响

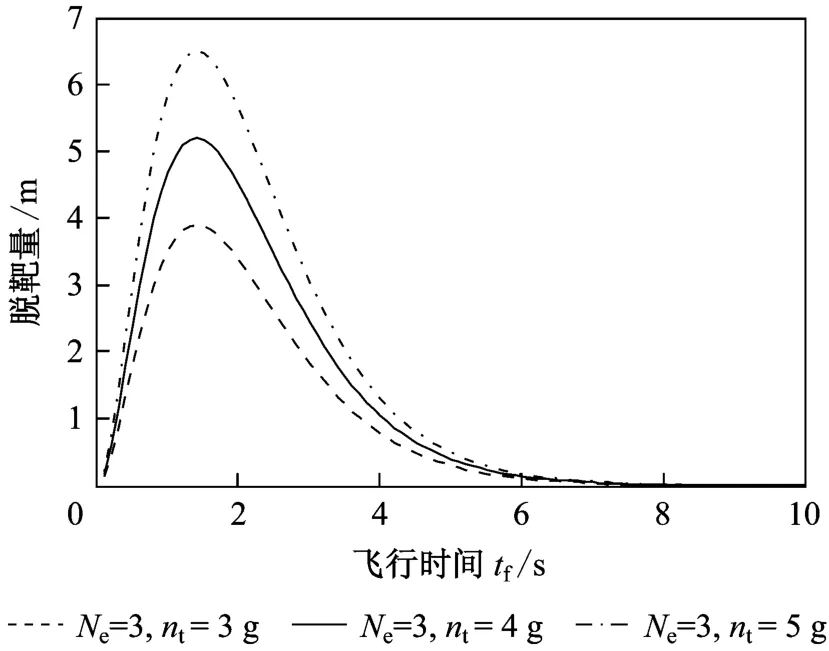
图2 目标机动对脱靶量的影响

从图1和图2可以看出:

a)飞行初期脱靶量迅速增大至最大值,然后,随着飞行时间的增加,脱靶量响应逐渐收敛,直至趋向于0;

b)目标机动加速度的增大,脱靶量明显增大;

c)在脱靶量趋向于0之前,随着有效导航比的增大,脱靶量减小。

1.2 噪声因素的影响

若考虑闪烁噪声、距离独立噪声、接收机噪声的影响,则由这些因素所造成的RMS脱靶量可以分别表示为[5]

式中 :k GN 、k FN、k RN和有效导航比有关;ΦGN、ΦFN和ΦRN分别表示闪烁噪声、距离独立噪声和接收机热噪声的功率谱密度,对应的时间常数分别为TGN、TFN和 TRN,对应的标准偏差分别为 σGN、σFN和σRN,它们之间满足下列关系:

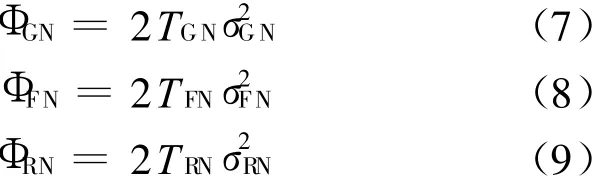
根据误差理论,这几个因素对脱靶量的影响可综合表示为

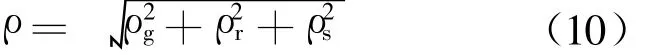
根据式(4)至式(10)进行仿真参数设计:当Ne=4时,kGN、kFN和 kRN的取值分别为 2.36、5.2和 90[5]。若 R TM=8 km,νc=5 km/s,ΦGN=1.5 m2/Hz,ΦFN=2 ×10-8rad2/Hz,ΦRN=2 ×10-8rad2/H z时,仿真结果如图 3所示。

从图3可以看出,随着制导时间常数的增大,由距离独立噪声和接收机噪声导致的RMS脱靶量逐渐增大;闪烁噪声造成的脱靶量随着制导时间常数的增大而逐渐减小。

1.3 延迟因素和导引头初始指向误差的影响

理论上,如果拦截弹拦截TBM 目标时,如果制导控制系统的反应时间符合理论设计值,不存在时间延迟,且执行机构能够提供足够的机动能力,那么拦截弹就一定能够命中目标。

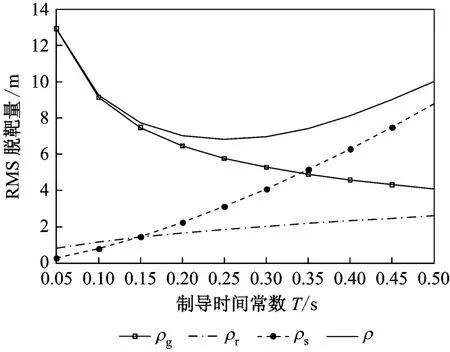
图3 不同噪声因素对脱靶量的影响

但实际上,拦截弹制导控制系统的系统反应时间往往大于理论设计值,即系统存在反应时间延迟,诸如导引头信息处理延迟,制导控制指令到达延迟和执行机构响应延迟等,这些延迟均影响导弹的制导精度。

另外,对于采用寻的制导的导弹,为了保护导引头天线在导弹飞行过程中不受机械的和热冲击的损坏,必须采用一定的能够满足气动外形要求的天线罩。天线罩在保护导引头的同时,也对导引头的测量性能产生了影响,从而影响了制导能力。带有天线罩的导引头测量目标的基本示意图如图4所示[6]。

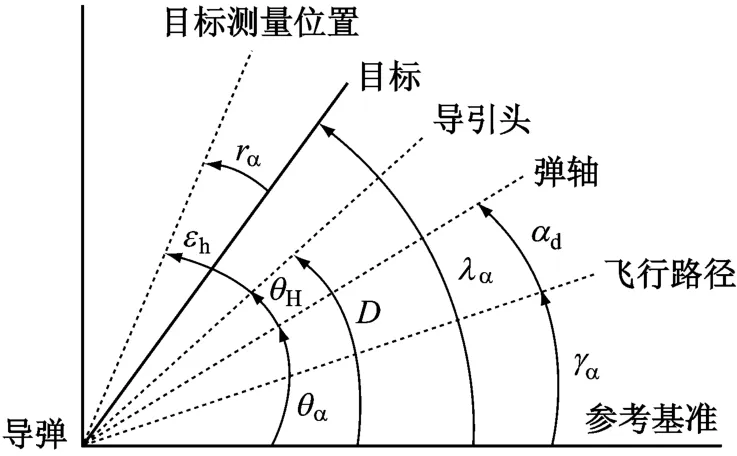
图4 天线罩的导引头测量目标的示意图

天线罩的折射角随导弹万向支架角θH而改变,天线罩的误差斜率k d就是折射角随万向支架角的变化速率,根据图4,可以得到天线罩误差斜率k d为

式中:rα是由天线罩折射角,也是由天线罩引起的测量误差角。

如果k d是一个不受 θH影响的常量,那么有

导引头初始指向误差:

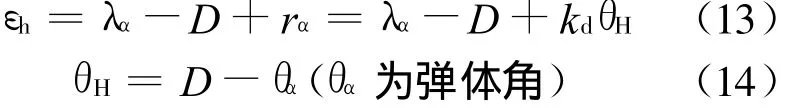
则有

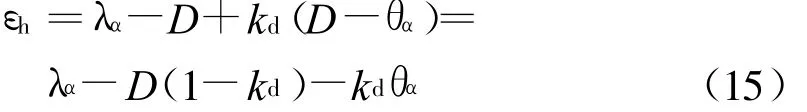
显然,当 k d=1 时,εh可近似为

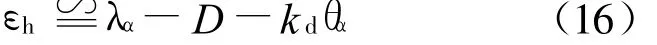
式中:D为导引头抛物面天线角;θα还可以由飞行路径角 γα和攻击角 αd共同表示,即

同时,导弹横向加速度a m、导弹速度V m和旋转周期常量Tα为

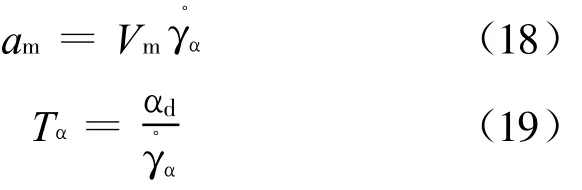
对式(16)微分,并与式(18)和式(19)联立,可得

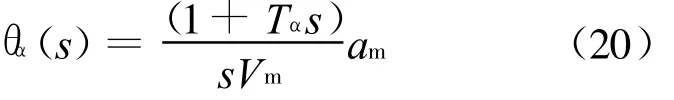
联立式(20)和式(16)可解得导引头初始指向误差 εh。

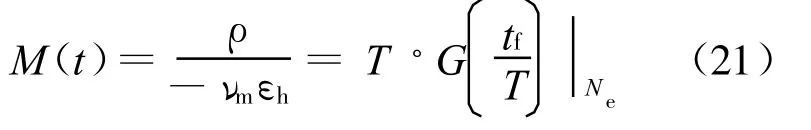
上述结论中,λ为视线转率;N e为有效导航比;νe为弹目相对速度;T为系统时间常数,代表了系统的延迟;n为系统阶数;n c为比例导引指令加速度;s为拉氏微分算子;tf为导弹飞行时间;νm为拦截弹速度。G(·)为T=1时系统的脱靶量随飞行时间变化的函数,也叫标称函数。

显然根据上述结论,在知道导弹初始指向角误差、有效导航比、标称函数、系统阶数和延迟的情况下,可较方便地求出由延迟引起的脱靶量。

文献[7]对这一结论进行了证明,并进一步得出当n→∞时,由纯延迟时间引起的脱靶量也遵循保罗的结论。文献[8]指出当初始指向角误差为εh=1/νm时,若不同飞行时间t f引起的终端脱靶量为根据式(21)可知,对不同的误差角,脱靶量等于

若考虑到导弹系统时间常数 T和制导时间与脱靶量的关系时,h0*(T N)=T其中:T N=t f/T,常被称为归一化制导时间。这样,在这种情况下,式(21)中的G(x)=x-0.5x2exp(-x)。

保罗在其著作中还指出:初始指向误差造成的标称脱靶量在不同导航比时,具有如下几种形式[4]:

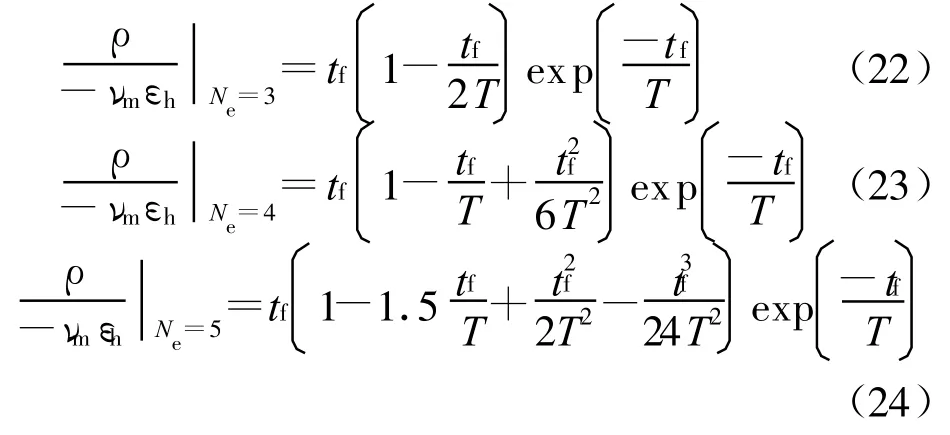
综上所述,结合文献[8]的观点,运用保罗的结论对初始指向误差一定的情况进行仿真分析,直观的反映系统延迟对于脱靶量的影响情况,仿真结果如图5、图6所示。初始指向误差对脱靶量的影响,如图7所示。

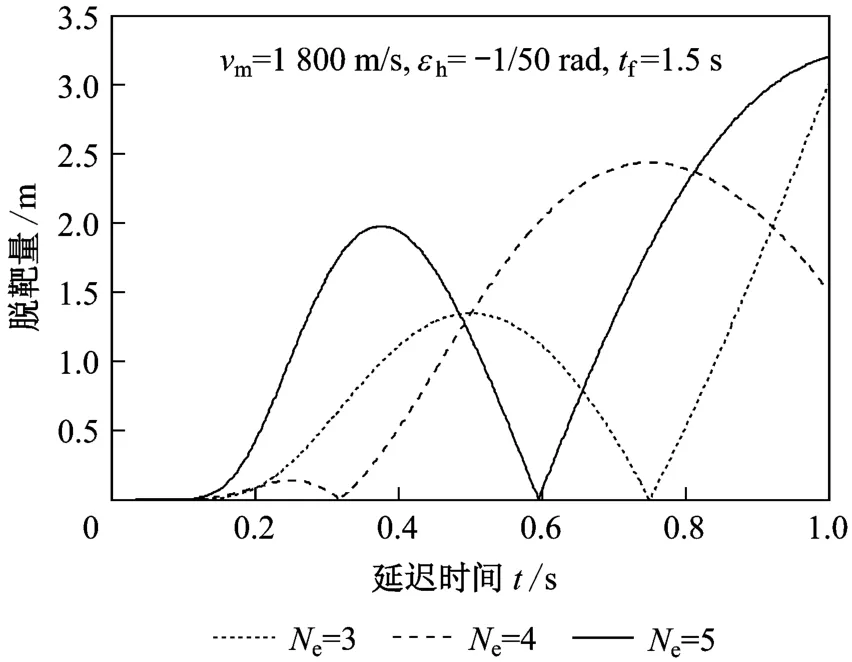
图5 延迟时间对脱靶量的影响

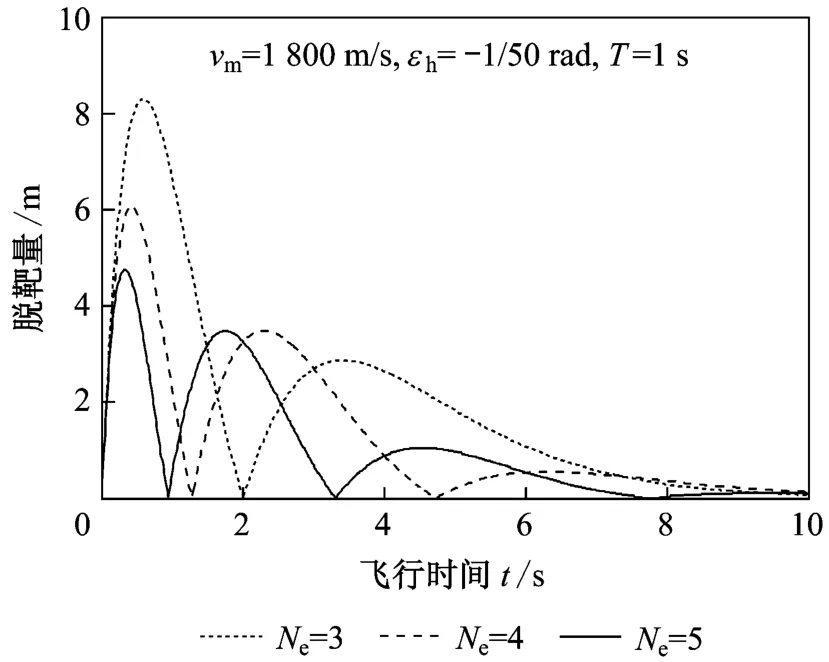
图6 脱靶量随飞行时间的变化

从图5中可以看出,参数不变的情况下,延迟时间越大,脱靶量越大;保持其它参数不变,仅改变有效导航比时,脱靶量起伏情况不定,如延迟时间为 0.25 s时,ρN e=4＜ρN e=3＜ρN e=5;当延迟时间为 0.6 s时 ,ρNe=5＜ρNe=3＜ρNe=4。

从图6可以看出,参数不变的情况下,随着飞行时间越长,脱靶量逐渐减小;保持其它参数不变,仅改变有效导航比时,脱靶量的起伏情况在不同的飞行时间也不一样。

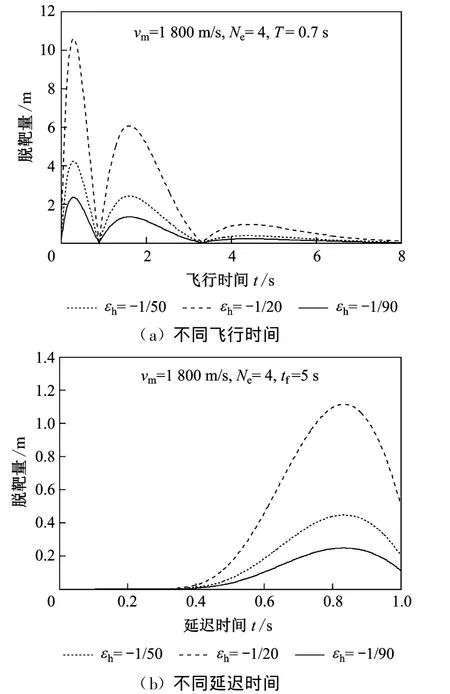
图7 初始指向误差对脱靶量的影响

从图7(a)可以看出,飞行时间一定的情况下,在初期,初始指向误差越大脱靶量显著增大;在飞行后期,不同大小的初始指向误差对脱靶量影响的差别不大。初始指向误差一定的情况下,随着飞行时间的增长,初始指向误差对脱靶量的影响迅速减小。

从图7(b)可以看出,在延迟时间一定的情况下,初始指向误差越大,脱靶量越大;在初始指向误差一定的情况下,延迟时间越大,脱靶量越大。

2 结束语

影响导弹脱靶量的因素较为复杂,脱靶量的变化还受到众多随机因素的影响,诸如天气因素等。如何将不确定的随机因素以合适的粒度加入到仿真中是值得进一步研究的问题。

[1] Shinar Josef,Turetsky V ladimir.Further Improved H om ing A ccuracy in Ballistic M issile Defense A-gainst Random ly Maneuvering[C].A IAA Guidance,Navigation,Control Conference and Exhibit,San Francisco,California,2005:2-6.

[2] Craig A.Phillips,James M.Chisholm.M issile Guidance and Control Challenges for Short Range Anti-airWarfare[J].A IAA,1995,3282:173.

[3] Nesline F.W.,Zarchan P..M iss Distance Dynamics in Hom ing M issiles[C].AIAA Guidance and Contro l Con ference.W ashington,1984,(8):84-98.

[4] Paul.Zarchan.Tacticaland Strategic M issile Guidance[J].Progress in Astronautics and Aeronautics,A IAA,Reston,Virginia,2007,219(5).

[5] Ding Chi-biao,Mao Shi-yi.M iss Distance Dynamic in A ctive Radar Homing M issiles[C].CIE International Conference of Radar,1996,(10):735-738.

[6] Susumu M iw a.Radome Effect on the M iss Distance of a Radar Hom ing M issile[J].Electronics and Communications,Japan,1998,81(7):14-21.

[7] 刘扬,张奕群,陈德源.系统延迟对脱靶量的影响研究[J].现代防御技术,2007,35(4):36-38.

[8] 丁赤飙,毛士艺.采用修正比例导引的雷达寻的导弹脱靶量研究[J].北京航空航天大学学报,1998,24(1):5-7.