调频步进信号回波的速度补偿

吴振凯

(上海无线电设备研究所,上海200090)

0 引言

调频步进信号作为一种高距离分辨信号,可以在不限制发射功率的同时,以较少的脉冲数和较小的瞬时信号带宽来合成一维高分辨距离像,使雷达导引头具备目标识别和精确打击的能力。然而这种方法的成像时间较长,相对速度使得目标在成像期间相对雷达导引头产生较大位移,引起散焦,严重影响了成像的真实度和准确度。为消除对成像的影响,必须对调频步进信号进行速度补偿。

1 相对速度对成像的影响

调频步进信号脉内采用chirp脉冲,由于线性调频信号对多普勒不敏感,典型信号参数下脉压后峰值的距离走动、耦合时移以及幅度加权效应可以忽略不计。但调频步进信号又属于频率步进信号体制,回波信号在脉压处理后仍保留着同频率步进信号相似的多普勒相位因子,其中一次相位因子使高分辨距离像的峰值发生距离走动,二次相位因子则会产生距离扩散现象[1～2],其数学表达式为

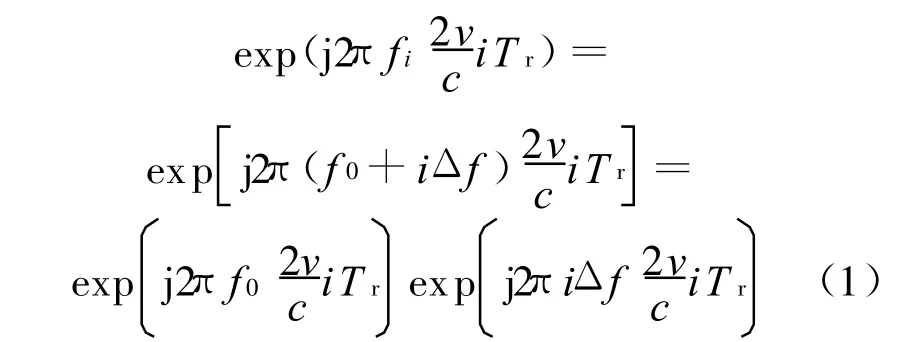
其中:

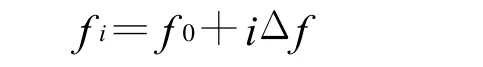
式中:fi为第i个脉冲的载频;f0为固定载频;Δf为跳频间隔;T r为脉冲重复周期;v为相对速度;c为光速。

该多普勒相位将连同距离高分辨相位exp(-j4πiΔfR/c),不加区分地一同进行 IFFT 处理,产生距离走动和距离扩展,其大小可分别通过式(2)和式(3)计算:

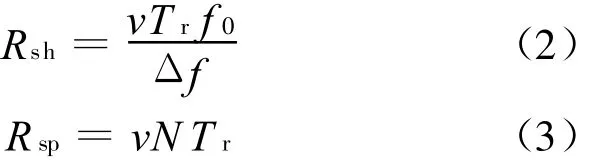
由于距离分辨率为δR=c/(2NΔf),故相应的走动距离分辨单元和扩展距离单元分别可以表示为

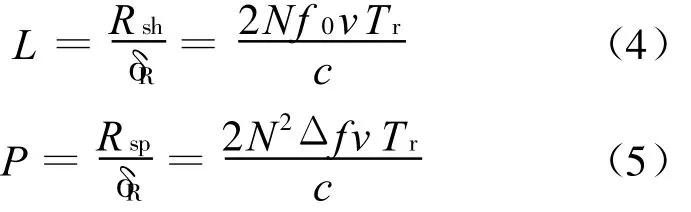
图1是典型参数下对运动点目标的成像仿真结果。具体仿真参数:固定载频 f0=13 GH z,信号调制带宽B=20MHz,跳频间隔Δf=8 MHz,积累脉冲数 N=64,脉冲宽度 T p=6.4μs,重频f r=7.5 kH z,I、Q数据采样率 f s=20 MHz,目标距离R=5 062m。如图所示,随着相对速度v的不断增大,目标峰值存在明显的距离走动和距离扩展现象。

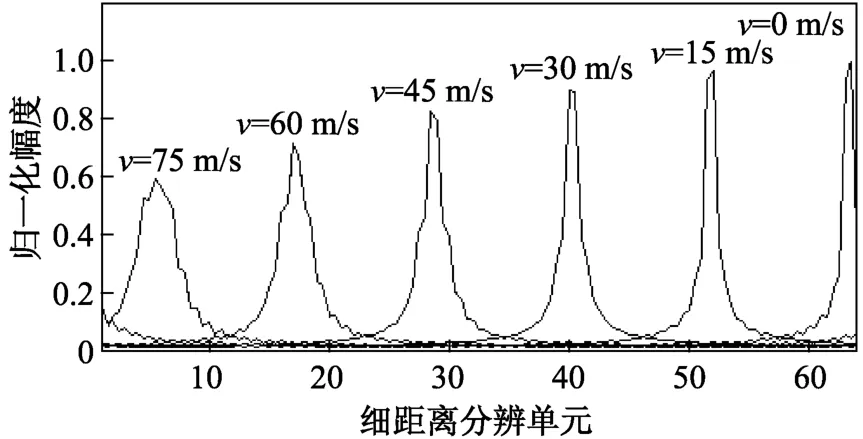
图1 IFFT后的距离走动和距离扩展

若要求距离扩散小于1/4个细距离分辨单元(P＜1/4),则需满足:

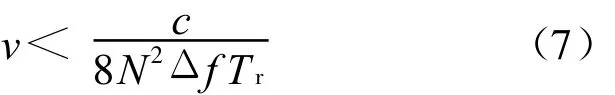
当v=15m/s时,峰值移动了10多个分辨单元,扩展现象还不是很明显;当v=75 m/s时,峰值移动已达到50多个分辨单元,而扩展现象也已十分明显。仿真结果表明,如果不进行速度补偿,调频步进信号成像的峰值将存在严重的距离走动和距离扩展现象,且对距离走动的速度补偿精度会较高。

在高距离分辨成像中,距离走动会直接带来测距不准甚至目标丢失等严重后果,而距离扩展对高分辨距离像也有着多种影响,比如信号幅度损失、测距精度以及距离分辨率等,必须将其控制在允许的范围内。若要求距离走动不超过半个细距离分辨单元(L＜1/2),则需满足:

对于上述典型信号参数设置,为避免出现距离走动和距离扩展,由式(6)和式(7)计算出允许的最大速度分别为0.68 m/s和17.17m/s,这使得调频步进信号成像的速度补偿精度要求高达米量级甚至更高。

2 调频步进信号的速度补偿方法

相对速度对调频步进信号成像的影响,主要是由多普勒相位因子产生的距离走动和距离扩展,只要通过某种方法测得相对速度,便可通过简单的乘法运算,在IFF T前的回波数据补偿掉该多普勒相位,完成调频步进信号的速度补偿。然而抑制距离走动的速度补偿精度高达米量级,这使得精确测速成为速度补偿的重点和难点。

国内外诸多学者提出并讨论了各种频率步进信号或调频步进信号的速度补偿方法,但对于实际的应用环境,这些方法都有着种种限制或不足之处。

2.1 频域相关法

频域相关法指的是在进行IFFT前,对相邻两帧回波数据求互相关,从相关输出的相位中提取速度信息[3～5]。

考虑单个点目标前后相邻的两帧脉冲回波,其内部脉冲回波基带相位分别为

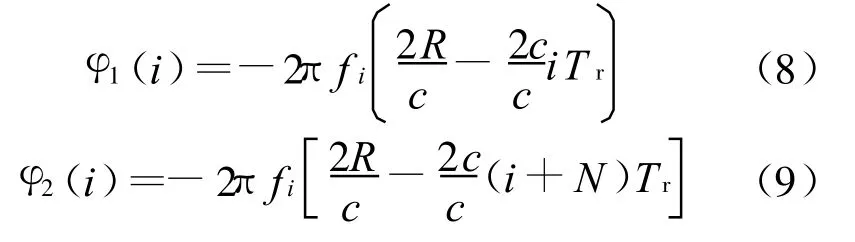
取两组回波数据相关的测度为

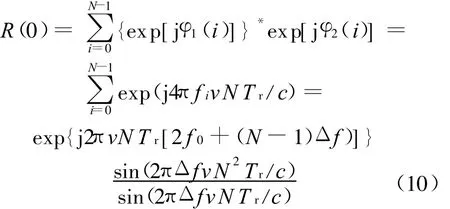
可见,R(0)的相位中包含了速度v的信息:

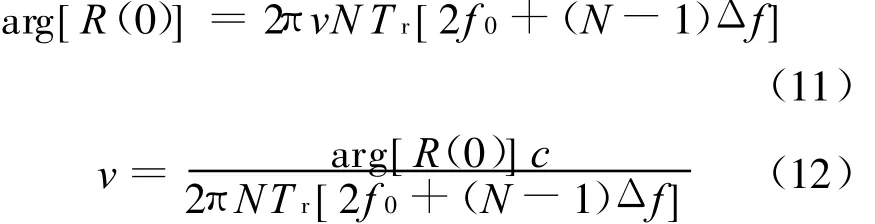
由于相位的周期为2π,因此 R(0)∈[-π,π],故测速不模糊范围为

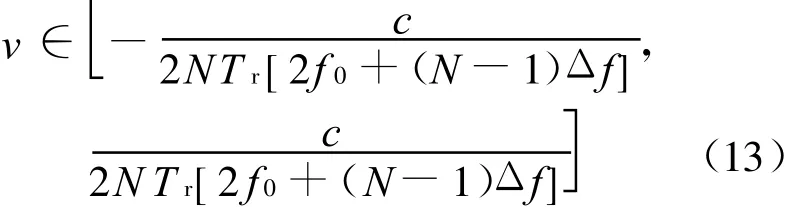
采用上节仿真中的典型参数设置,测速不模糊周期仅为1.77 m/s。因此,该测速方法虽然估计精度较高、运算量小,但测速不模糊范围较小,实用性较差。

2.2 时域相关法

时域相关法是对IFFT后的相邻两帧回波数据进行互相关处理,利用两帧之间对应脉冲的相关,求出目标在两帧之间的走动,进而利用走动距离和目标速度之间的关系估计目标速度。由于是在对脉压和IFFT处理后进行的信号处理,故该方法抗噪性能较好。

由式(8)、(9)可知,相邻两帧回波数据的相位差为

对应的延时和距离差分别为

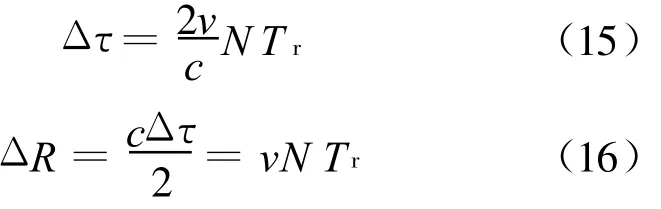
该距离差使得两帧回波的高分辨距离像中,峰值位置相差的分辨单元格为

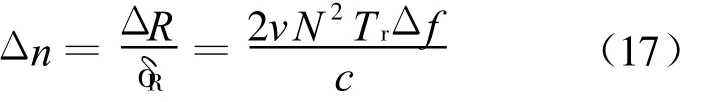
其中:

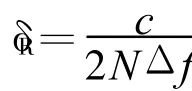
式中:δR为细距离分辨单元率。

在通过IFFT合成高分辨距离像后,通过读取两帧回波中同一目标峰值相差的距离分辨单元数Δn,便可推算出速度信息:

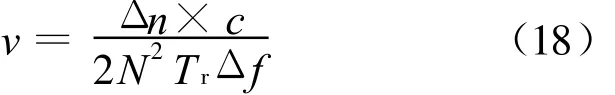
当|Δn|＜N/2时无模糊,故有测速不模糊范围和测速精度:

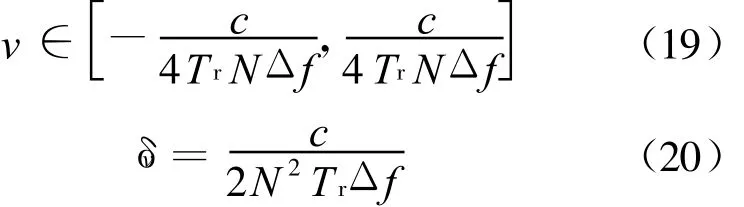
在上节仿真中的典型参数设置下,测速不模糊周期为2 930 m/s,但测速精度仅有45.8 m/s。所以,时域相关法虽然测速范围较大,抗噪性能好,但精度较低,虽然可以通过补零IFFT加以改善测速精度,但仍不能达到米量级的补偿精度,距离走动无法消除。

2.3 最小熵值法

最小熵值法是一种闭环迭代算法。熵是信息论中的概念,表征不确定度的大小,熵值越大,像越无序。该方法首先将一幅经过速度补偿的高分辨距离像H(i)进行时域幅度归一化成H 1(i),定义图像熵为

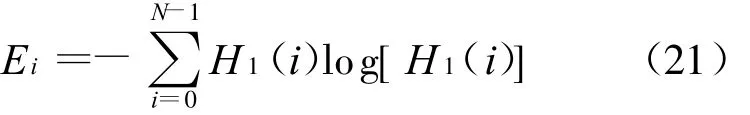
当速度估计值等于实际值时,图像熵达到最小值。最小熵值法是一个具有反馈能力的闭环系统,它能自适应地使系统熵值达到最小。该方法运算量大、速度慢,且易受噪声影响,很难在实际系统中应用[3,5]。

2.4 升降频信号处理法

该方法发射一对升降频脉冲序列,利用升降频信号回波中特殊的相位关系可以获取速度信息。升降频脉冲序列指的是一对跳频斜率相反的脉冲序列,升频脉冲序列载频从 f0步进至 f0+(N-1)Δf,降频脉冲序列载频从 f0+(N-1)Δf递减至 f0。

利用升降频信号获取速度信息的具体方法不止一种,一般是通过构造某种关于升降频回波数据的函数,在一定范围内进行速度搜索,当构造函数达到全局极小值或全局极小值时,即确定最佳补偿速度。这类方法主要有最小脉组相位差分法、最小脉组误差法、最大脉组乘积求和法以及最大脉组矢量相加求和法等[2,4-7]。

以最大脉组乘积求和法为例,说明该类方法的测速原理。发射升降频脉冲序列,回波按发射顺序排列,设S1(i)、S2(i)为升降频脉冲序列IFFT前经速度补偿后的回波数据:

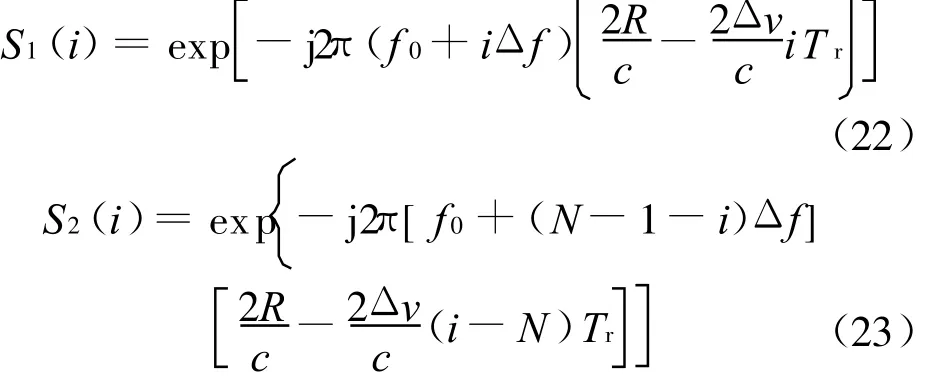
定义脉组乘积求和函数:

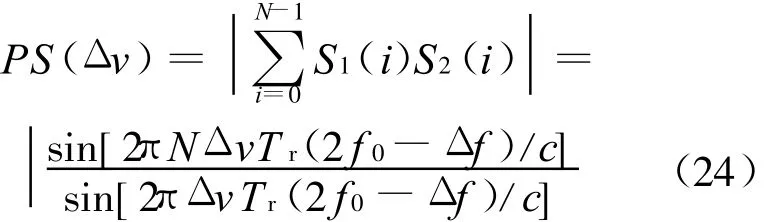
如图2所示,脉组乘积求和函数在Δv=0时取到全局最大值,此时的估计速度即为真实速度。可见,利用脉组误差函数进行速度估计的过程,实质上就是沿着图2的曲线搜索全局最大峰值的过程。

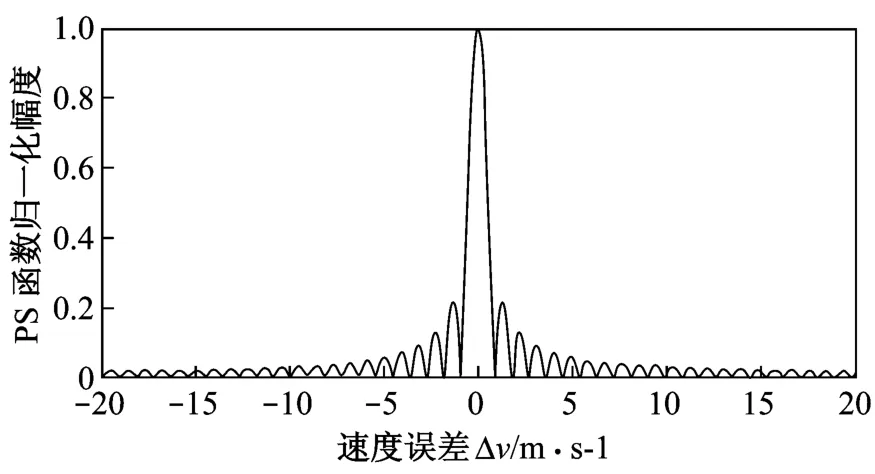
图2 脉组乘积求和函数

对最大脉组乘积求和法进行每个信噪比下50次M onte-Carlo实验,得到调频步进信号的速度估计误差随接收机输出端信噪比变化的曲线图。如图3所示,当信噪比高于-10 dB时,均能获得准确估计速度,但信噪比低于-15 dB时,此法已不能搜索到正确估计速度,出现较大偏差。由于调频步进信号通过脉冲压缩可以获得一定信噪比增益,可知此法对普通频率步进信号下的信噪比要求将会更高。

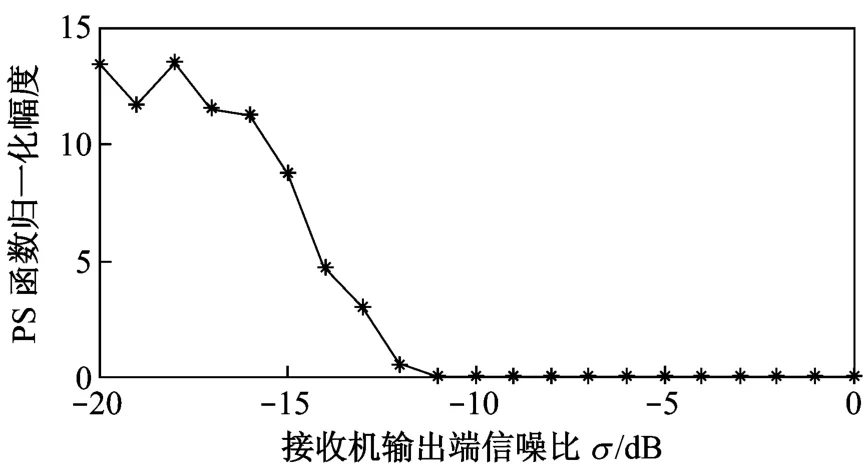
图3 不同信噪比下的测速误差曲线

该类速度估计方法主要存在如下几个问题:

a)升降频信号处理法对信噪比要求较高,在小信噪比情况下容易搜索到局部极大极小值,甚至因噪声引起的极值会超过真值对应的函数极值,而导致速度搜索失败,虽然最大脉组乘积求和法,最大脉组矢量相加求和法较前两者在小信噪比下的测速性能有一定程度的改善,但离实际应用仍有一定差距;

b)为了尽可能搜索到全局最小值,搜索步长应小于最小峰值宽度。由于构造函数的最小峰值宽度较窄,因此搜索步长较小,导致搜索时间较长,不利于实时处理;

c)构造函数关于速度真值呈对称分布,因此在搜索起始值距离真值较远时无法确定Δv的符号,即无法判断搜索方向,错误的搜索方向将使计算量和搜索时间的倍增。

2.5 线性调频脉冲序列测速法

目前,各种通过处理调频步进信号本身来获取速度信息的方法,都有着这样那样的局限性和不足之处,不妨采用普通的脉冲多普勒方法来精确测量相对速度,实现调频步进信号的速度补偿。首先发射一组线性调频脉冲序列,通过脉冲压缩和相参处理,可以提高信噪比并获取速度信息。脉冲重复频率和积累脉冲数决定测速不模糊范围和测速精度,若要求较高的测速精度,PRF不能过高,可以适当提高积累的脉冲数,而PRF过低也会造成测速不模糊范围太小。因此需要合理设计脉冲重复频率和积累脉冲数,以同时保证一定的测速范围和要求的测速精度。实际应用时,通过粗速度估计值可对测速模糊进行解模糊处理,从而确定真实而精确的相对速度。

在进行线性调频信号的参数设计时,除了要满足测速范围和测速精度的要求,还需要尽量保持和调频步进信号的参数一致,以利于硬件系统的实现。设计的信号参数,如表1所示。

表1 线性调频信号(LFM)和调频步进信号(LMFS)的参数设计

(1)测速不模糊范围与测速精度

对于脉冲多普勒体制,脉冲重复频率 fr和积累脉冲数N决定了测速不模糊范围和测速精度:

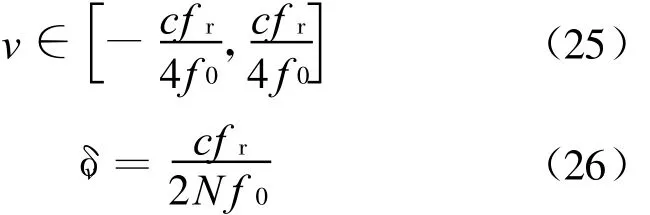
通过式(25)、(26)可计算出表1所示信号参数下,线性调频信号的测速不模糊范围为-57.7 m/s～57.7 m/s,测速精度为 0.9 m/s,而由式(6)、(7)所计算出该信号参数下的调频步进信号的速度补偿精度要求为Δv＜0.9m/s。因此,测速精度可以满足系统要求,而测速模糊可以通过粗速度估计解决,并要求粗速度估计误差小于57.7 m/s,而该精度的粗速度估计是不难实现的。

(2)抗噪声性能

在与前文中的时域相关测速法一样,该方法的测速是在脉冲压缩和相参积累后进行的,相比采用相参积累前的其他测速方法,显然具有较好的抗噪声性能。脉冲压缩和相参积累处理的信噪比增益分别为

式中:D=T p B为信号的时宽带宽积,即压缩比;N为积累因子。

由式(27)、(28),表1参数下的线性调频信号通过脉冲压缩和相参积累分别可以获得18 dB和21 dB的信噪比增益。假设检测信噪比为12 dB,则折算到接收机输出端的信噪比要求仅为-27 dB。

(3)作用距离与兼容性

两种体制下的作用距离是否匹配关系到该测速方案的实际可行性。作用距离的计算可通过如下的雷达方程计算:

式中:SNR为检测信噪比;Pt为雷达发射峰值功率;T p为脉冲宽度;G为天线增益;λ为雷达工作波长;σ为目标散射截面积;N为积累因子;R为目标距离;k为玻耳兹曼常数;T0为温度;Fn为接收机等效噪声系数;L a为大气衰减因子;L s为各种系统损耗。

由表1可以看出,除了积累脉冲数,两种体制下的信号参数完全一致。在杂波背景较弱或无杂波背景的条件下,由于线性调频信号的积累脉冲数更多,所以其作用距离更远,可以完成调频步进信号作用距离内的全程测速。在强杂波背景的条件下,由于调频步进信号具有更高的距离分辨率,相当于减小了检测单元中的杂波能量,从而提高了信杂比。抗杂波性能的差异,使得强杂波背景下线性调频信号的作用距离可能小于调频步进信号,做不到全程测速,只能在近距离下完成目标的速度检测,以进行调频步进信号的速度补偿。

此外,两种体制下信号参数的一致度也使得两者系统设计相互兼容,大大简化了系统复杂性,实际中的模式切换较为方便。

图4是为调频步进信号速度补偿的仿真结果,其中图4(a)为无相对速度条件下的高分辨距离像,而图4(b)、图4(c)为存在相对速度的情况下,速度补偿前后的高分辨距离像。仿真中的相对速度为326.7m/s,粗估计速度为300 m/s,通过线性调频脉冲序列的测速,得到的估计速度为326.3m/s。如图所示,相对运动使距离像产生了严重的距离走动和距离扩展,经过精确的速度补偿,距离走动和距离扩展均被消除,峰值位置准确,无幅度衰弱、分辨率下降的现象,速度补偿效果良好。

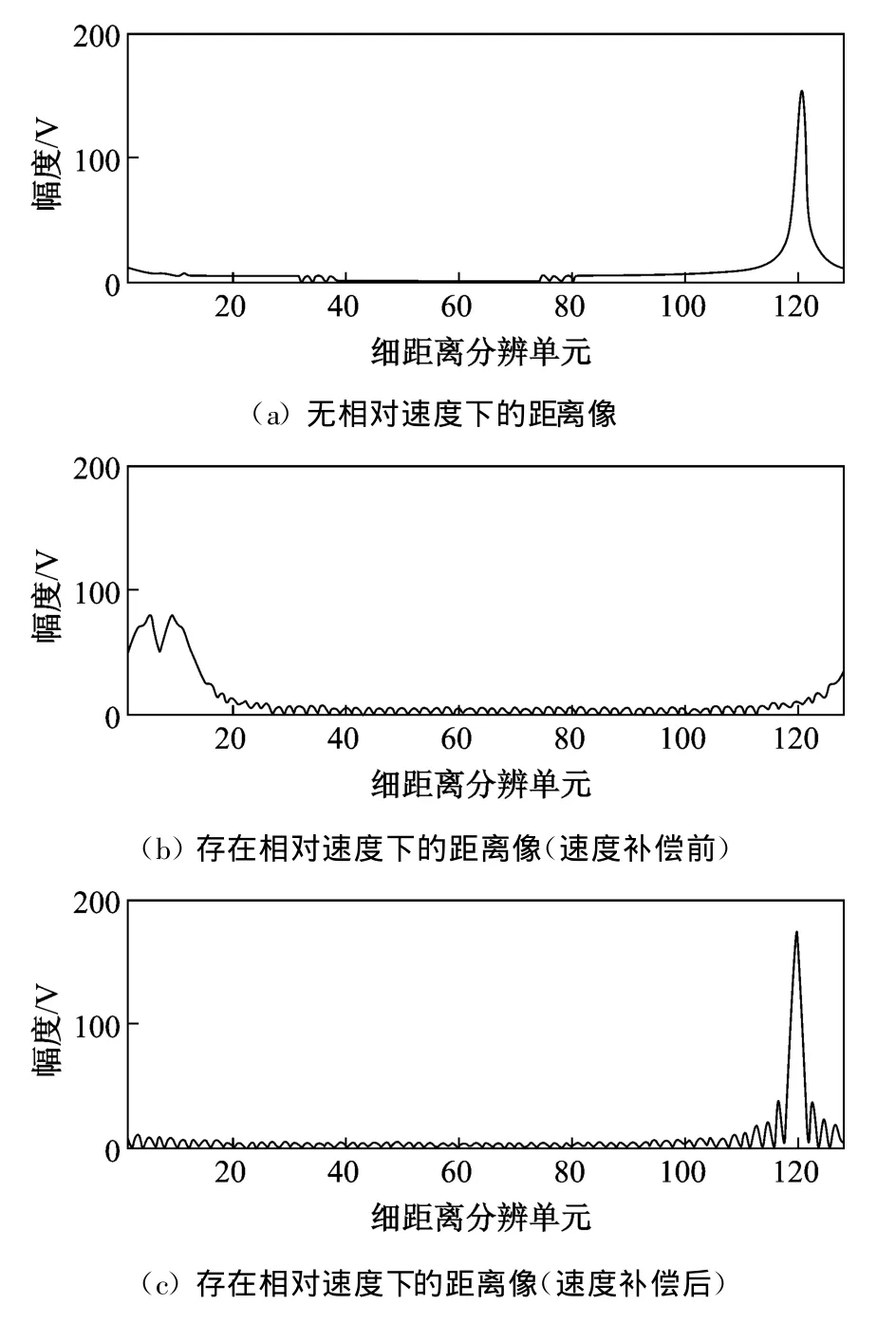
图4 调频步进信号速度补偿的仿真结果

利用线性调频信号测速并进行速度补偿的方法,虽然增加了在发射成像信号前的系统工作量,但通过合理的参数选择,降低了系统复杂性,在杂波背景较弱的情况下可完成全程测速,并实现精确的速度补偿。

仿真结果证明:该方法可以达到速度补偿的精度要求,并具有较好的抗噪性能。实际应用时,可以利用一组线性调频脉冲序列测得的精确速度对其后多帧调频步进信号回波进行速度补偿,以缩短每次成像的时间。

3 总结

本文从相对速度对调频步进信号成像的影响入手,仿真分析了多普勒相位因子产生的距离走动和距离扩展现象,并得出速度补偿精度要求的数学表达式。在综合讨论了目前各种调频步进信号速度补偿方法利弊的基础上,提出使用线性调频信号进行速度补偿具有精度高、抗噪性能好等优点,并利用合理选择的信号参数进行了仿真,仿真结果印证了该方法的正确性和实用性。

[1] 龙腾.频率步进雷达信号的多普勒性能分析[J].现代雷达,1996,18(2):31-37.

[2] 刘铮,张守宏.步进频率雷达目标的运动参数估计[J].电子学报,2000,28(3):43-45.

[3] 蒋楠稚,王毛路,李少洪,毛士艺.频率步进脉冲距离高分辨一维成像速度补偿分析[J].电子科学学刊,1999,21(5):665-670.

[4] 刘宏伟,王俊,张守宏.运动目标环境下步进频率信号的设计与处理[J].西安电子科技大学学报,1997,24(增):75-81.

[5] 王绍江.频率步进雷达导引头信号处理系统研究[D].南京,南京理工大学,2007.

[6] 何志毅.合成宽带毫米波雷达导引头的理论及实现[D].北京,中国航天二院,2002.

[7] 石志广,付强.一种运动目标距离像的速度补偿方法[J].制导与引信,2002,23(3):14-17.