毫米波/红外复合制导目标融合跟踪算法
李相平, 王光复, 谢志敏
(1.海军航空工程学院电子信息工程系,山东烟台264001;2.总参气象局,北京100081)
0 引言
毫米波/红外复合制导目标跟踪属于多传感器信息融合范畴,集中式和分布式是两种主要的融合结构。其中,分布式结构具有造价低、可靠性高、通信量小等特点。该结构先由自己的数据处理器产生局部多目标跟踪航迹,然后把处理后的信息送至融合中心,融合中心根据各节点的航迹数据完成航迹关联和航迹融合,形成全局估计。对于分布式多传感器系统来说,有两个重要的问题需解决:
a)如何决定来自不同传感器的哪条航迹代表着同一目标,这是航迹关联问题;
b)在确定了两个传感器对同一目标的位置和状态估计后,如何对两个传感器的数据进行融合,这是航迹融合问题。
许多学者对航迹融合算法进行了深入细致的研究:
a)文献[1]介绍了在传感器航迹估计误差不相关假设下简单加权航迹融合算法(SF);
b)文献[2]提出了一种基于最大似然比的最优航迹融合算法(M L);
c)文献[3]介绍了由于共同过程噪声的引入,各传感器局部估计误差相关的基础上的协方差加权航迹融合算法;
d)文献[4]出于简化计算复杂度,提出了一种自适应航迹融合算法;
e)文献[5]提出了分层融合算法,该算法在传感器与融合中心高速通信且局部航迹估计时刻与全局航迹融合时刻的相同条件下的航迹融合解是最优的。
本文在上述基础上给出一种改进的算法。
1 简单航迹融合算法
假设分布式多传感器信息融合系统由传感器1和传感器2组成,目标运动状态模型为
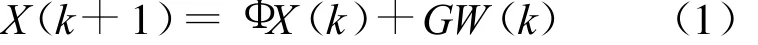
传感器i∈[1,2],k时刻的量测Zi(k)服从如下线性模型:
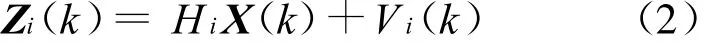
式中:X(k)为状态向量;Φ为一步状态转移矩阵;Z i(k)为传感器i的量测向量;Hi(k)为传感器i的量测矩阵;W(k),Vi(k)为统计独立的零均值高斯白噪声;方差分别为Qi和Ri。
假设不同传感器航迹估计误差是统计独立的,则两传感器的加权融合算法为
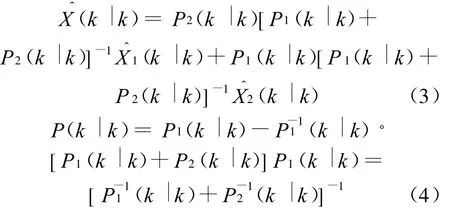
2 互协方差加权融合算法
与加权融合算法完全忽略误差相关性不同,在互协方差加权融合算法中则考虑了这种相关性对融合估计的影响,两传感器的融合算法如下:
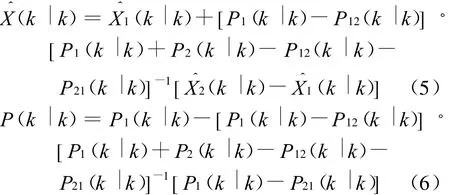
∀i=1,2,传感器i的航迹状态估计为基于截至k时刻的最新量测序列Zi(k)的最小均方误差估计,假设对应传感器i,滤波增益为K i(k),则关于互协方差有如下的递推关系[4]:
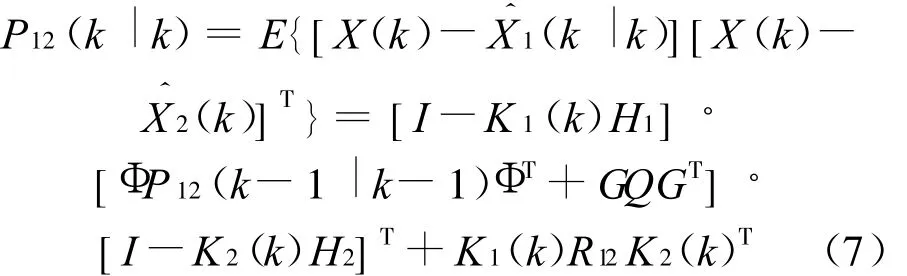
式中:R12为两传感器的量测误差互协方差。
3 毫米波与红外融合跟踪
上面介绍了两种基本的航迹融合算法,本文中的毫米波与红外复合制导目标跟踪,采用分布式融合结构。但是对于红外传感器,由于只有角跟踪问题[6],文中采用一种基于部分反馈的毫米波与红外融合模型,同时考虑到导弹在搜索和攻击目标过程中,毫米波与红外传感器不同程度地受到各种干扰,给出一种基于环境变量的航迹融合算法[7]。基本思想:当毫米波与红外传感器同时工作均未受到干扰时,毫米波与红外子跟踪滤波器各自产生局部估计,将各自得到的航迹送至融合中心,融合中心对局部航迹采用简单加权因子方法进行融合,得到全局航迹,然后将融合得到的预测状态即协方差阵反馈到红外子跟踪滤波器,作为它的预测状态及其协方差;当两传感器其中之一受到干扰时,受干扰传感器信息不可用,融合输出为未受到干扰的传感器产生的局部航迹。融合模型如图1所示。
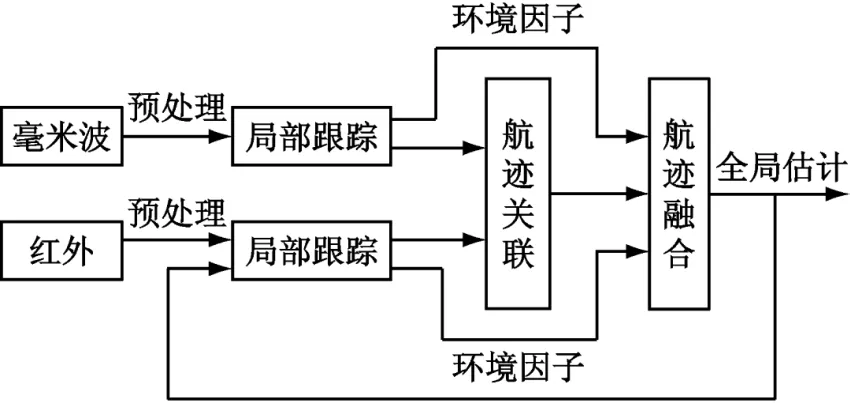
图1 毫米波/红外复合制导融合跟踪模型
(1)局部估计
为了简化讨论,假设目标运动模型如式(1)所示,目标的状态向量 X(k)是在极坐标系下定义的,量测方程为
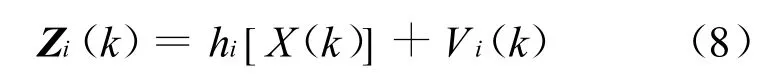
式中:i对应符号R和I,分别代表毫米波雷达和红外传感器。量测向量分别为Z R(k)=[r(k),θR(k),φR(k)]T,Z I(k)=[θI(k),φI(k)]T。量测矩阵如下:

式中:r(k),θR(k)和 φR(k)为毫米波雷达的量测距离、俯仰角和方位角;θI(k),φI(k)为红外传感器的量测俯仰角和方位角;V R和V I(k)为毫米波雷达和红外传感器的量测误差向量,假定是相互独立的零均值高斯白噪声,协方差阵分别为RR(k)和 RI(k)。
由于量测矩阵是非线性的,采用扩展卡尔曼滤波算法,可以得到两传感器的状态估计和协方差更新为
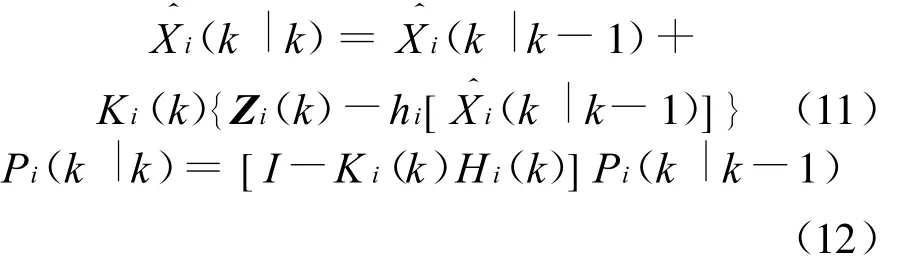
式中:H i(k)是传感器i线性化后的雅可比矩阵,i意义同上。
(2)航迹融合
假设在航迹融合之前,已经完成了局部航迹在时间和空间上的配准,同时对两传感器代表同一目标的两条航迹完成了关联。当毫米波雷达与红外同时工作时,对上面的两个局部估计结果进行融合。融合过程中,利用传感器受到干扰情况等环境变量来描述传感器数据的可用性。在单传感器局部跟踪过程中,定义新息序列为
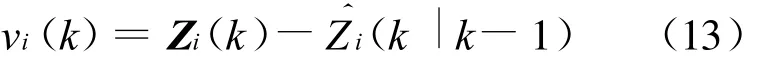
相应的新息协方差为
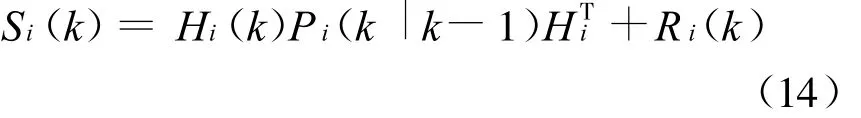
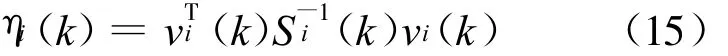
假设vi(k)∈Rl,l为传感器的观测向量维数,则ηi(k)理论上服从自由度为 l的χ2分布。按照 χ2分布规律,可以定义不同置信水平上的传感器有效域:预先定义阈值 γi,如果 ηi(k)≥γi,则传感器量测信息不可用,在融合过程中忽略该传感器的信息;如果 ηi(k)<γi,则认为该传感器工作正常,在融合过程中采用该传感器的信息。从文献[7]可知,对于毫米波雷达传感器,其量测向量包括距离、俯仰角和方位角,即 l=3,考虑95%的置信水平,γR=7.8;对于红外传感器,其量测向量包括俯仰角和方位角,即l=2,同样考虑95%的置信水平,γI=5.9。
在环境变量计算的基础上,考虑导引头传感器的时效性,利用加权因子融合两传感器的估计结果[8]:
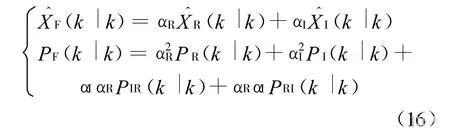
a)如果ηR<7.8,ηI<5.9,则两传感器信息都可以用
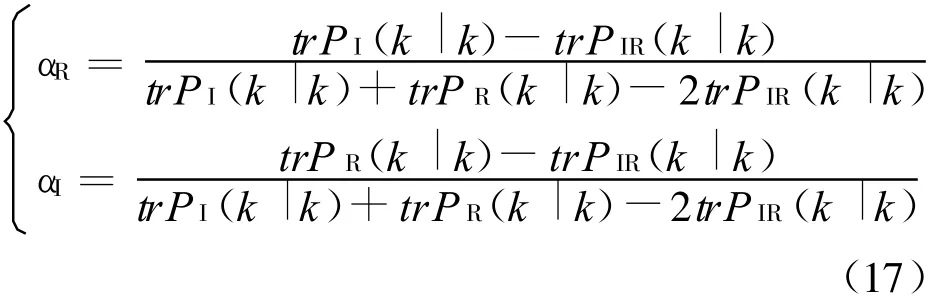
b)如果 ηR<7.8,ηI≥5.9,则红外信息不可用,融合输出为毫米波雷达局部估计结果:

c)如果 ηR≥7.8,ηI<5.9,则毫米波雷达信息不可用,输出为红外局部估计结果:

d)如果 ηR≥7.8,ηI≥5.9,则两传感器信息都不可用,融合输出为状态预测结果:
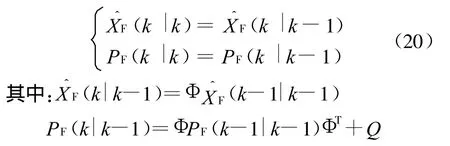
当毫米波雷达和红外传感器均未受干扰时,两传感器信息都可用,引入部分反馈后,红外传感器的局部状态估计算法如下:
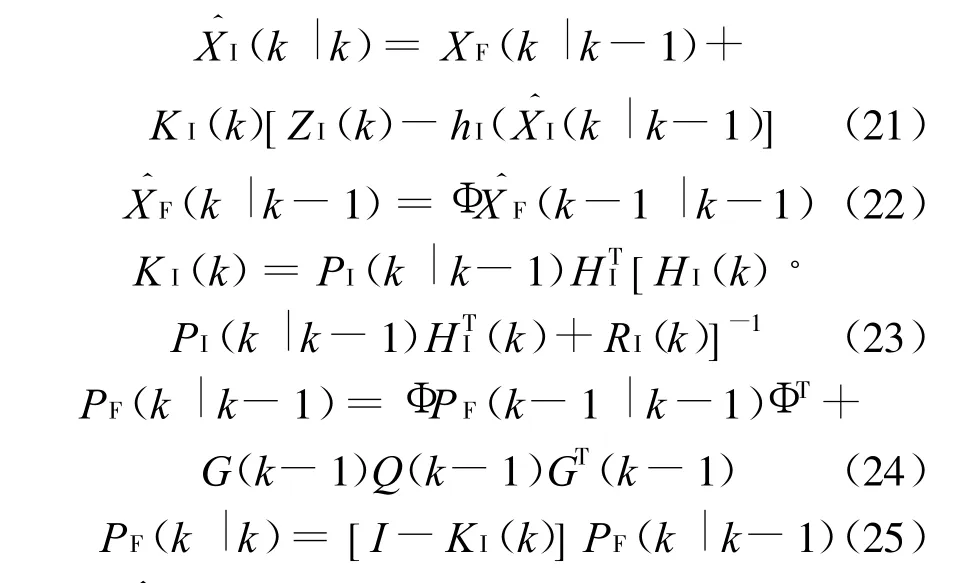
4 仿真分析
为了简化问题,仿真中假设导弹与目标在同一水平面或同一高度上,即目标在水平面上运动,毫米波传感器提供距离和方位信息,红外传感器提供方位信息,目标初始位置为(2 000 m,10 000 m),初始速度为(0,15 m/s),在前200 s内目标以初始速度作匀速直线运动,在t=200 s时目标以加速度(0.1 m/s2,0.1 m/s2)作匀加速转向运动,持续时间100 s,在t=(300~500)s内目标继续作匀速直线运动。假设毫米波和红外传感器数据已融合到中心融合节点时刻和节点坐标系中,同步后采样周期 T M=T I=1 s,毫米波量测噪声标准差分别为:距离维σM r=500 m,方位角σMθ2 m rad;红外传感器的方位角量测噪声标准差为 σIθ=0.1 m rad,过程噪声为 0.05m/s2。假设在目标运动过程中,在 t=(300~330)s内,红外传感器受到干扰,其量测噪声方差增大10倍,而毫米波信息不变。分别采用简单加权融合算法(SF)和文中的算法进行100次蒙特卡罗仿真,结果如下所示。
从图2,图3,图4,图5可以看出:首先,无论是位置均方误差还是速度均方误差,融合后的航迹均方根误差都比单个传感器跟踪均方误差要小,同时,由于EKF滤波涉及到模型线性化更严重,导致红外跟踪误差较毫米波雷达跟踪误差要大;其次,当红外传感器未受干扰时,在目标运动过程中,无论是目标位置均方误差还是速度均方误差,两种融合算法融合精度相当,但在t=(300~330)s内,红外传感器受到干扰的过程中,采用简单加权融合算法位置和速度均方误差明显增大,融合跟踪精度下降,而改进的算法由于引入环境变量因子,能自适应地判断干扰的出现,在此期间,舍弃红外传感器信息,只利用毫米波传感器信息,融合估计精度明显优于SF算法,在干扰消除后,SF算法估计误差收敛到与改进的算法结果,因此改进的算法在保持融合精度的同时,提高了导引头的抗干扰能力。
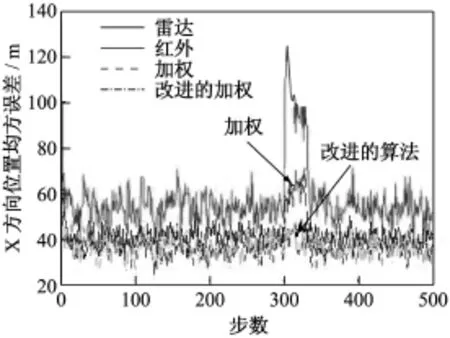
图2 X方向位置均方误差图
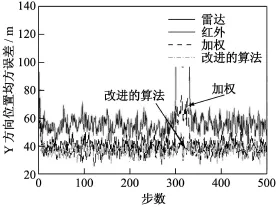
图3 Y方向位置均方误差
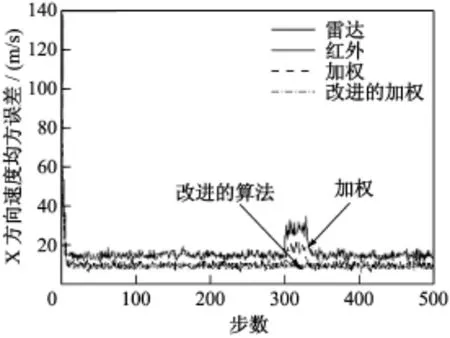
图4 X方向速度均方误差图
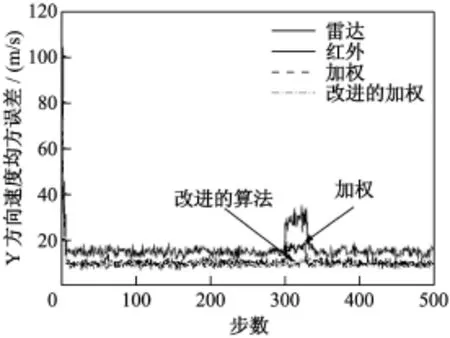
图5 Y方向速度均方误差
5 结束语
航迹融合是多传感器信息融合的关键问题,本文研究了毫米波/红外复合制导目标融合跟踪问题,介绍了简单加权融合和互协方差加权融合,考虑到红外传感器只有角度量测信息,在应有部分反馈的基础上,给出一种基于环境变量的融合跟踪模型。且进行了相应的仿真实验,仿真结果表明,改进的算法保证全局融合精度的同时,提高了系统抗干扰能力,表明了该算法的有效性。
[1] Singer R,Kanyuck.Computer Control of Multiple Site Track Correlation Automatic[J].1971,(7):455-464.
[2] R.K.Saha,K.C.Chang.An Efficient A lgorithm for M ultisensor Track Fusion[J].IEEE Transaction on Aerospace and Electronic Systems,1992,34(1):200-210.
[3] Bar-Sha lom Y,Camp L.The Effect o f Common Process Noise on the Tw o-Sensor Fused-Track Covariance[J].IEEE Trans on Aerospace Electronic System,1986,22(6):803-805.
[4] Beugnon C,Singh T,Linas J et al.An Adap tive T rack Fusion in a M u ltisensor Environment[C].Paris:ISIFConference,2000.
[5] C.Y.Chong,S.Mori,K.C.Chang.Distributed Mu ltitarget Mu ltisensor Tracking in Mu ltitarget-Mu ltisensor T racking:Adanced A pplications[M].Y.Bar-Shalom,ed,Boston,MA:A rtech H ouse,1990:247-294.
[6] S.C.Nardone,V.J.A lidela.Observability C riteria for Bearing-on ly Target Motion Analysis[J].IEEE Transaction on Aerospaceand Electronic Systems,1982,17(2):162-166.
[7] Yuan Q,Dong C Y,W ang Q et al.An Adap tive Fusion A lgorithm Based on ANFIS for Radar/In frared System[J].Expert Systems with App lications.2009,36:111-120.
[8] 孙书利,崔平远.两种传感器最优信息融合Kalman滤波器及其在跟踪系统中的应用[J].宇航学报,2003,24(2):206-209.

