沥青路面Top-Down 裂缝的断裂力学分析

赵延庆,王抒红,周长红,谭忆秋

长期以来,人们认为沥青路面疲劳开裂是由于路面结构在行车荷载作用下沥青层底部产生拉应力,从而在沥青层底部形成裂缝,这些裂缝向上扩展,最终形成贯穿于整个沥青层的裂缝.然而近年来越来越多的研究发现,沥青路面的疲劳开裂也可能起始于路表,这些路表裂缝在行车荷载作用下不断地向下扩展, 这类裂缝称为“从上到下的疲劳裂缝(Top-Dow n fatigue cracking)”.从上到下的疲劳裂缝已逐渐被国内外的道路工作者认为是沥青路面的一种主要病害形式[1].断裂力学是对带裂缝的路面结构进行分析的常用方法.由于现场沥青路面结构中沥青混合料的力学性质受温度和行车速度的影响,沥青混合料力学性质的变化将影响路面结构中以及裂缝尖端的应力分布情况,进而影响裂缝的产生和扩展.我国目前的沥青路面设计方法中采用抗压回弹模量作为沥青混合料的基本力学参数[2],但抗压回弹模量不能很好地反映温度及行车速度对沥青混合料力学性质的影响[3],从而限制了分析的客观性.本文对典型的沥青路面结构建立了有限元模型,利用沥青混合料动态模量主曲线和时间-温度位移因子来综合反映温度和行车速度对沥青混合料力学参数的影响,根据断裂力学方法,分析了在随时间和空间变化的移动荷载作用下沥青路面Top-Dow n裂缝的开裂机理,并分析了基层类型对其的影响,为更科学地进行路面结构分析和设计提供基础.

1 路面结构分析模型及参数

1.1 材料力学参数

对图1 所示的路面结构进行分析,对沥青混合料层,采用动态模量主曲线和时间-温度位移因子作为其基本力学参数.动态模量主曲线描述荷载作用频率对材料性质的影响,时间-温度位移因子描述了温度对材料性质的影响,这样动态模量主曲线和时间-温度位移因子合起来就可描述温度和荷载频率的变化对混合料力学性质的影响[4].图1 所示路面结构中沥青混合料层取Superpave20 混合料,其动态模量试验在5 个温度和7 个频率下进行,试验过程和结果见文献[5] .据时间-温度等效原理,对试验数据进行拟合,就可得到动态模量主曲线及时间-温度位移因子,数值分析过程和结果见文献[3,6] .

为利用动态模量主曲线进行路面结构力学分析,需要确定不同行车速度在路面结构内产生的荷载频率.这可以用“等效厚度法”来实现[4].利用等效厚度法预测路面结构内应力脉冲时间如下:

式中:t为应力脉冲时间,可以和荷载频率相互转化;vs为行车速度;Leff为有效长度,为确定Leff,等效厚度法将路面土基以上各层结构转化为厚度为有效厚度he,模量为土基模量的一层.等效厚度法假设在转化后的当量路面结构中应力沿45°角向下直线扩散.在某一深度处的Leff即为该深度处应力影响区的水平长度.详细的计算公式及步骤见文献[ 4,7] .这样就可以在有限元方法中利用等效厚度法、沥青混合料的动态模量主曲线及时间-温度位移因子来分析温度和行车速度对沥青路面Top-Dow n 开裂的影响.沥青混合料面层以外其他各层材料的力学参数取值如图1 所示.针对两种基层类型进行分析.基层采用粒料材料时,E=300 MPa, μ=0.35,基层为半刚性材料时,E=2 000 M Pa,μ=0.25.

1.2 有限元模型

如图1 所示.沥青层表面存在一长度为a的Top-Dow n 裂缝.为提高分析效率,将路面结构近似为平面应变问题的四层连续体系[8].据弹性断裂力学,在行车荷载作用下裂缝尖端的应力场确定如下[9]:

式中:r,θ为以裂缝尖端为原点的极坐标;Fij(θ)为θ的函数[9];KⅠ和KⅡ分别为Ⅰ型(张开型)和Ⅱ型(剪切型)应力强度因子.应力强度因子表征了裂缝尖端应力场的强度,可以被看作为促使裂缝扩展的驱动力.由式(2)可知,在裂缝尖端,各应力分量具有r-1/2奇异性,当r趋于0 时,各应力分量均趋于无穷大.但事实上,在裂缝尖端总存在一个断裂进程区(fracture process zone),在进程区内,材料具有非线性变形行为,基于线弹性断裂力学的式(2)将不再适用.Castell 等的研究表明[10],裂缝长度大于0.7 cm 时,断裂进程区和K主导区相比尺寸足够小,式(2)仍能给出较精确的结果.本文分别对不同工况下5 种裂缝长度(2.5,5.0,10.0,15.0 和17.5 cm)进行分析.

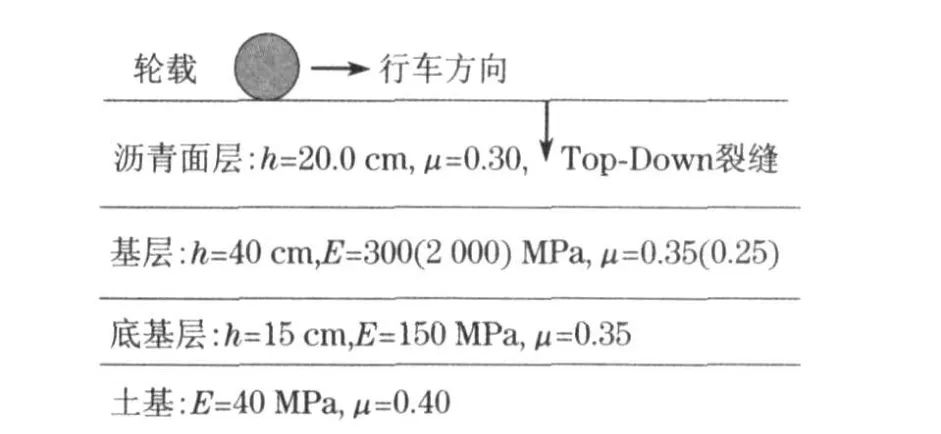
图1 沥青路面结构Fig.1 Asphalt pavement structure

荷载采用移动荷载模式,如图1 所示.将轮载在时间和空间上进行离散.随着时间的推移,轮载不断地向前移动,在某一时刻,轮载面积上荷载的分布认为是0 到π区间内的正弦波形,用以模拟实际行车荷载作用下在路表产生的“钟型”分布荷载[11].在轮载两侧,荷载为零,在中间位置达到峰值,荷载峰值取0.7 MPa.不同的车速通过让轮载在单位时间内移动不同的距离来实现.

为了分析轮载从远离裂缝处驶向裂缝,并逐渐离开裂缝整个过程中裂尖应力强度因子的变化过程,采用的限元模型尺寸必需足够大,才能保证得到裂尖应力强度因子完整的变化过程,并消除边界条件的影响.通过试分析,本文确定有限元模型的长度为14 m,深度为5 m.对有限元模型采用四边形平面应变8 节点等参元进行离散.由于在裂缝尖端存在应力场的奇异性,在裂缝尖端设置奇异单元[9],即将平面应变单元一个边上的三个节点重叠,退化为三角形单元.重叠节点位于裂尖上,并将和裂尖相连的两边中间节点移动到靠裂尖1/4 距离处,以满足裂缝尖端的r-1/2奇异性[9].为保证分析结果的准确性,在裂缝尖端附件的单元需足够小.本文裂尖单元尺寸取0.2 mm,经试算能满足精度要求.另外为了提高计算精度和效率,在模型两侧及底面采用无限元进行离散.最终将整个模型离散为15 975 个单元,共50 233 个节点.需要指出的是,除了行车荷载,由于温度变化引起的温度应力对沥青路面力学响应也有影响.但由于温度应力作用时间长,此时由沥青混合料粘弹性质引起的应力松弛现象将起重要作用.另外温度较高时,采用基于沥青混合料粘弹塑性本构关系的断裂力学进行分析将更合适,但这种方法目前在道路工程中的应用研究还很不成熟,本文仍采用弹性断裂力学分析,不考虑温度应力的影响.

2 分析结果

2.1 应力强度因子变化分析

利用以上建立的有限元模型,分析了温度为10,25 和40 ℃,行车速度为40,70 和100 km·h-1时裂尖应力强度因子的变化情况.分析了在每一种温度和车速组合下,5 种不同裂缝长度(2.5,5,10,15 和17.5 cm)下裂尖应力强度因子的变化规律.篇幅所限,只在图2 和图3 中给出了当基层采用粒料材料,行车速度为70 km· h-1,温度为25 ℃时,轮载移动到距裂缝不同距离时应力强度因子的分析结果.图中的正、负横坐标分别表示轮载位于裂缝的右边和左边.图中KⅠ的正值表示裂尖承受拉伸作用,这种作用有可能使裂缝进一步扩展.KⅠ的负值表示裂尖承受压缩作用,这种作用对裂缝扩展不起作用.KⅡ对应于剪切型开裂,故无论KⅡ是正值还是负值,都将对裂缝扩展起作用.

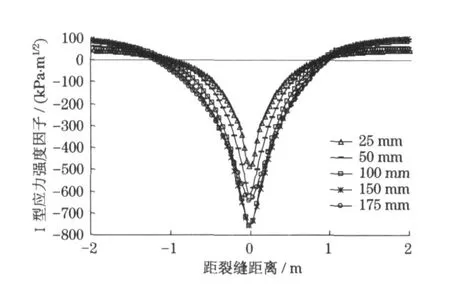
图2 Ⅰ型应力强度因子变化曲线Fig.2 Changes of mode Ⅰstress intensity factor

图3 Ⅱ型应力强度因子变化曲线Fig.3 Changes of mode Ⅱstress intensity factor

由图2 知,当轮载从远处驶向裂缝时,在裂尖产生正的KⅠ,并且KⅠ随轮载逐渐靠近裂缝而增加.KⅠ达到峰值后开始下降,并逐渐变为负值.KⅠ达到峰值时轮载和裂缝的距离随工况不同而有所不同.当轮载位于裂缝正上方(对称加载位置)时,负值KⅠ达到峰值.轮载离开裂缝过程中KⅠ的变化和驶向裂缝过程中有对称性.可见,轮载经过Top-Dow n 裂缝一次会产生两个正的KⅠ峰值,且大小相等.对于II型应力强度因子,当荷载在裂缝左侧时,KⅡ为负值.当荷载在裂缝右侧时,KⅡ为正值.对于KⅡ,有两个关键作用位置,即轮载左侧和右侧边缘分别位于裂缝上方(非对称加载位置)时,KⅡ达到峰值.这两个位置处KⅡ的绝对值相等,但方向相反.当轮载位于裂缝正上方时,KⅡ为0.对其他工况及基层采用半刚性材料时,KⅠ和KⅡ的分析也得到类似的结论.

2.2 各因素影响规律

由以上分析可知,当轮载经过T op-Dow n 裂缝时,裂尖应力强度因子经历连续变化过程,并且KⅠ和KⅡ都出现两个对裂缝扩展起作用的峰值,且两个峰值数值大小相同.表1 和表2 中给出了当基层分别采用粒料材料和半刚性材料时,在各种温度、行车速度和裂缝长度下KⅠ和KⅡ的峰值,对于KⅡ,表中只给出了正值的峰值.可见,从整体上说,随着裂缝长度的增加,KⅠ和KⅡ峰值增加.只有当裂缝长度较大(大于15 cm)时,在某些工况下,KⅠ和KⅡ的峰值随裂缝长度的增加而稍有减小.温度对裂尖应力强度因子有显著的影响,在各种工况下,KⅠ和KⅡ的峰值随着温度的升高而减小.但这并不意味着裂缝在温度较高时不易扩展,因为随着温度的升高,沥青混合料的抗开裂能力也在减弱[12],较小的应力强度因子也会造成裂缝的扩展.行车速度对应力强度因子峰值的影响不大,随着车速的增加,KⅠ和KⅡ的峰值均稍有增加.虽然行车速度对应力强度因子峰值的影响不大,但对其作用频率却有显著的影响.图4 中给出了温度为25 ℃裂缝长度为10 cm 时,各种车速下KⅠ的时程曲线,由于对称性,图中只给出了轮载在裂缝左侧运动时KⅠ的正值部分.为便于比较,图4 中将不同行车速度下KⅠ正值开始出现的时间定位0 时刻.可见随车速的增加,应力强度因子的作用时间变短,即频率增加.研究表明,随着应力强度因子作用频率的增加,沥青混合料抵抗裂缝扩展的能力提高[12],上面的分析得到路面结构裂尖应力强度因子峰值随车速变化不大,所以较慢的行车速度会加速Top-Dow n 裂缝的扩展.比较表1 和表2 中的数据可知,从整体上说,对于相同的温度、车速及裂缝长度,采用半刚性基层和采用粒料基层相比可以降低Top-Dow n 裂缝的裂尖应力强度因子.对于本文分析的各种工况,采用半刚性基层时,KⅠ的峰值平均降低了7.1%,KⅡ的峰值平均降低了25.2%.综合分析表1 和表2 中各工况下的数据,可知当温度较低且裂缝较短时,张开型应力强度因子KⅠ对裂缝扩展的贡献较大.而随着温度的升高和裂缝长度的增加,剪切型应力强度因子KⅡ的贡献逐渐增加,这在基层采用粒料材料时更为明显,例如当温度为

40 ℃.,裂缝长度为17.5cm 时,KⅠ和KⅡ的峰值分别为62.8 和187.5 kPa·m1/2,此时剪切型应力强度因子成为裂缝扩展的主要驱动力.

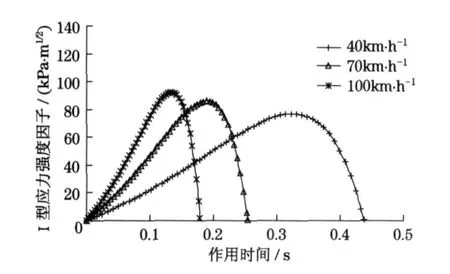
图4 不同车速下K Ⅰ时程曲线Fig.4 K Ⅰ-time curves at various vehicle speeds

由以上分析知,KⅠ和KⅡ峰值随裂缝长度的增加而增加,这意味着Top-Down 裂缝的扩展将越来越快,故当路表出现Top-Dow n 裂缝时,应及时维修,以免裂缝加速扩展.由于较慢的行车速度会加速Top-Dow n裂缝扩展,故在正常路段应保持一定的行车速度,而在上坡、收费站附近车速较慢的路段,应考虑采用改性沥青混合料等抗裂性能较好的材料.采用半刚性基层可降低Top-Dow n 裂缝的裂尖应力强度因子,但在工程设计中还应考虑半刚性基层自身容易开裂,并形成反射裂缝的特点,进行综合优化设计.

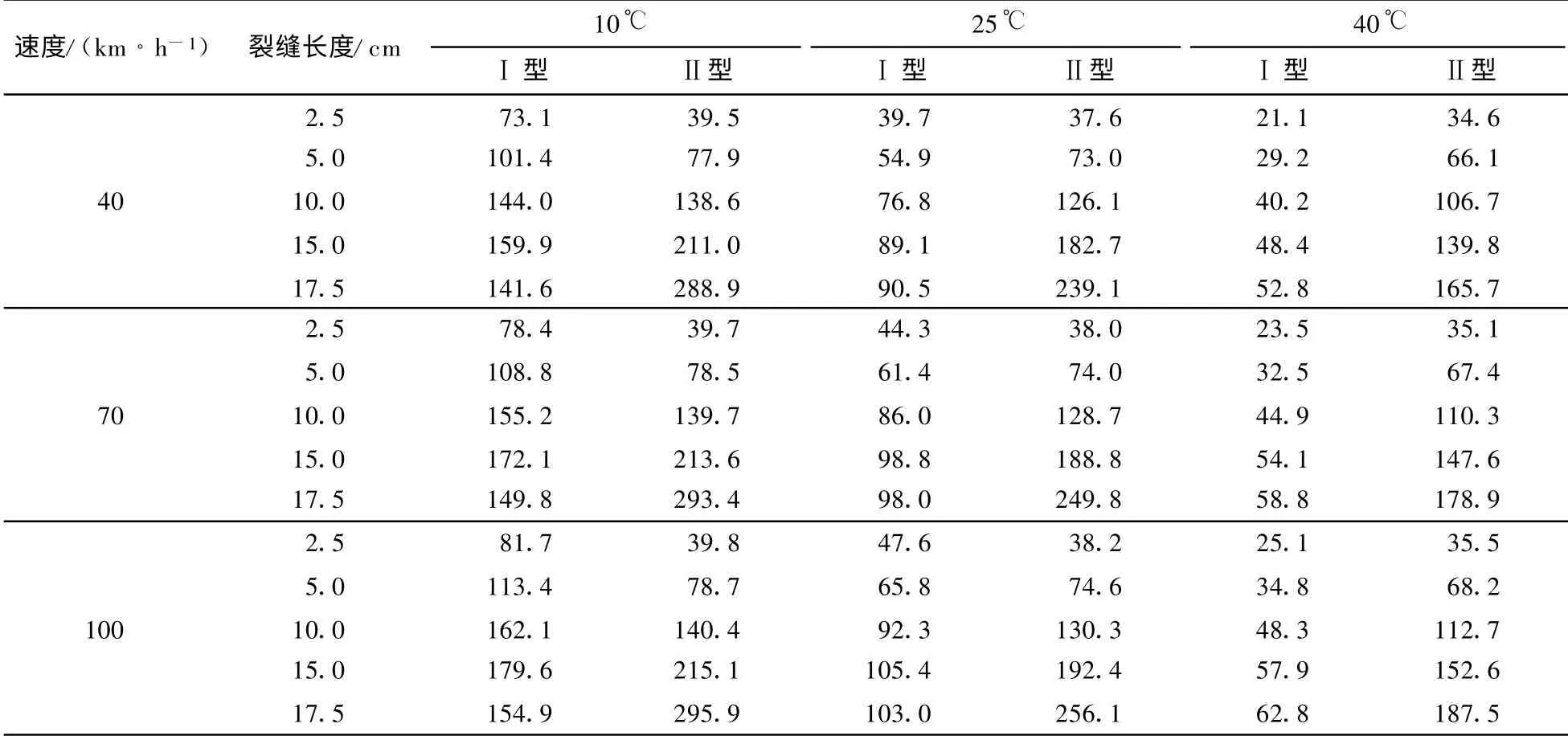
表1 各种工况下应力强度因子峰值(粒料基层,单位:kPa·m1/2)Tab.1 Peak stress intensity factors at various conditions(granular base, unit:kPa·m1/2)

3 结论

(1)在有限元方法中利用沥青混合料的动态模量主曲线和时间-温度位移因子来考虑温度和行车速度的影响,采用移动荷载模式,根据断裂力学的方法,可以更科学地分析沥青路面Top-Dow n 裂缝应力强度因子的影响因素和变化规律.

表2 各种工况下应力强度因子峰值(半刚性基层, 单位:kPa·m1/2)Tab.2 Peak stress intensity factors at various conditions(semi-rigid base,unit:kPa·m1/2)

(2)轮载经过Top-Dow n 裂缝一次,KⅠ和KⅡ均会产生两个数值相等的峰值,且KⅡ的两个峰值方向相反.

(3)从整体上说,随着裂缝长度的增加和温度的减小,KⅠ和KⅡ峰值增加.随车速的增加,应力强度因子的作用频率增加,较慢的行车速度会加速Top-Dow n 裂缝的扩展.

(4)从整体上说,和采用粒料基层相比,在相同工况下采用半刚性基层可以降低Top-Dow n 裂缝的裂尖应力强度因子,KⅡ峰值降低的幅度更大.

(5)当温度较低且裂缝较短时,KⅠ对裂缝扩展的贡献较大,而随着温度升高和裂缝长度增加,KⅡ的贡献逐渐增加, 这在基层采用粒料材料时更为明显.

[ 1] Roque R,Birgisson B, Drakos C,et al.Development and field evaluation of energy-based criteria for top-dow n cracking performance of hot mix asphalt[ J] .Journal of the A ssociation of A sphalt Paving Technologists,2004,73:229.

[ 2] 中华人民共和国交通部.JTG D50—2006 公路沥青路面设计规范[ S] .北京:人民交通出版社,2006.Ministry of C om munications of P R C.JTG D50—2006 Specification of design of highw ay asphalt pavement[ S] .Beijing:China Communications Press,2006.

[ 3] 赵延庆,薛成,黄荣华.沥青混合料抗压回弹模量与动态模量的比较分析[ J] .武汉理工大学学报,2007,29(12):105.ZH AO Yanqing,XUE C heng, H UANG Ronghua.C om parison of com pressive resilient modulus and dynam ic modulus of asphalt mixtures [ J] .Journal of Wuhan University of Technology,2007,29(12):105.

[ 4] Applied Research Associates.Guide for m echanistic-empirical design of new and rehabilitated pavement structures[ R] .Washington D C:Transportation Research Board, 2004.

[ 5] 赵延庆,叶勤,文健.围压对沥青混合料动态模量的影响[ J] .重庆交通大学学报,2007, 26(6):96.ZH AO Yanqing, YE Qin, WEN Jian.Effects of confining pressure on dynamic modulus of asphalt mixtures[ J] .Journal of Chongqing Jiaotong University,2007,26(6):96.

[ 6] 赵延庆,吴剑,文健.沥青混合料动态模量及其主曲线的确定与分析[ J] .公路,2006,8:98.ZH AO Yanqing, WU Jian, WEN Jian.Determination and analysis of dynamic modulus of asphalt mixture and its master curve[ J] .Highw ay,2006,8:98.

[ 7] 赵延庆,潘友强.沥青路面结构内荷载作用频率分布与变化规律的研究[ J] .长沙交通学院学报,2007,23(4):7.ZH AO Yanqing, PAN Youqiang.Study on loading frequency distribution and changes w ithin asphalt pavements[ J] .Journal Of Changsha Communications University ,2007, 23(4):7.

[ 8] 郑健龙,周志刚,张起森.沥青路面抗裂设计理论与方法[ M] .北京:人民交通出版社,2002.ZH ENG Jianlong, ZH OU Zhigang, ZH ANG Qisen.Design theory and method for cracking resistance of asphalt pavements[ M] .Beijing:China Communications Press,2002.

[ 9] Gross D,Seelig T.Fracture mechanics:w ith an introduction to micromechanics[ M] .New York:Springer Press,2006.

[ 10] Castell M , Ing raffea A, Irw in L.Fatigue crack grow th in pavements [ J] .Journal of Transpor tation Engineering,American Society of Civil Engineering,2000, 26(4):283.

[ 11] 孙立军.沥青路面结构行为理论[ M] .北京:人民交通出版社,2005.SUN Lijun.Structure behavior study for asphalt pavements[ M] .Beijing:China Communications Press,2005.

[ 12] Sulaim an S, Stock A.T he use of fracture mechanics for the evaluation of asphalt mixes[ J] .Journal of the A ssociation of Asphalt Paving Technologists,1995,64:500.