地下水源热泵取水引起颗粒运动的理论分析

王松庆,张 旭,高 军

(同济大学 机械工程学院,上海200092)

地下水源热泵由于节能效果好,近些年在国内得到了广泛的应用,尤其在地下水富裕地区,地下水源热泵更成为工程首选.但地下水源热泵在使用过程中还存在一些问题,如井水含沙.如把含沙的地下水长期不断地抽到热泵机组中,会造成热泵机组的损坏,更可能会由于长期抽水而造成取水井的井壁坍塌,造成地下水源热泵无法继续使用的严重后果[1].地下水源热泵如果采用同井回灌的运行方式,反复地抽、灌也会引起井壁周围的细颗粒介质的重组[2].如果不对这些问题进行研究加以解决,地下水源热泵的使用将受到限制,不利于地下水源热泵的发展.国内外对由于渗流引起土壤颗粒运动的研究主要集中在堤坝管涌现象和颗粒运输等方面.李守德等[3]对土坝发生管涌这一过程的渗流场空间性状进行了研究;周健等[4]对砂土管涌的发展过程进行了模拟;Sterpi[5]对由于渗流引起细颗粒侵蚀和运输进行了实验研究.但对于地下水源热泵取水对含水层颗粒影响的研究较少.本文对地下水源热泵地下取水引起含水层土体颗粒运动进行了理论研究和算例分析,为解决地下水源热泵取水井长期运行后可能出现的井壁坍塌和井壁周围颗粒重组等问题提供了理论依据,对合理有效使用地下水源热泵具有重要的指导意义.

1 颗粒受力状况分析

地下水源热泵的地下取水装置示意图如图1 所示.图中箭头方向表示地下水的渗流方向,A点表示土体颗粒,颗粒由于同时受到多种力的共同作用,在满足某种条件时从固体骨架上脱落,脱落后的颗粒随着水流一起运动,一部分会再次沉积下来,重新成为固体骨架的一部分,另一部分则随着水流(流量为Q)进入热泵机组.对A点处的土体颗粒进行受力分析,研究其运动是极为重要的.本文中颗粒受到的作用力主要考虑了由渗流引起的拖曳力、粘着力、自身的有效重度和升力等.

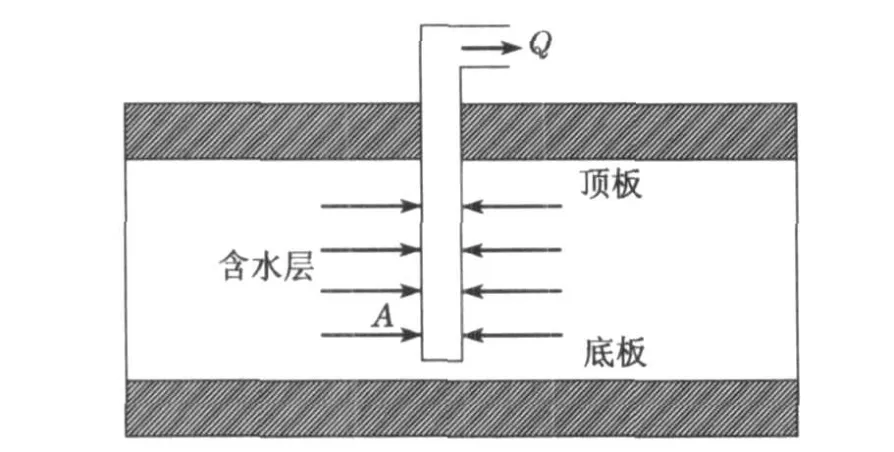
图1 地下水源热泵地下取水示意图Fig.1 Schematic diagram of pumping groundwater with groundwater source heat pump system

1.1 拖曳力

假设土体颗粒为球形颗粒,半径为r,且球面光滑无粗糙.在渗流方向上由于渗流引起的作用在颗粒上的拖曳力可表示为[6-7]

式中:γf为水的重度,N·m-3;V为颗粒的体积,m3;当其为完整球体时,,其中r为球形颗粒的半径,m;J为水力坡度,量纲为一.

如果把含水层假想成由大量Poiseulle 孔隙管体组成,其示意图如图2 所示.假设颗粒脱离与管体中壁面切应力有关,其计算式可以表示为[8-9]

式中,τ为切应力,Pa.当τ=τcr时,土体颗粒开始运动,τcr为临界切应力.

图2 由不同粒径颗粒组成的假想的孔隙管体示意图Fig.2 Schematic diagram of hypothetical poretubes composed by particles with different diameters

1.2 粘着力

对于含有粘性土的含水层,研究粘着力对颗粒从固体骨架脱离的影响是十分重要的.Sharma 认为粘着力主要是作用在颗粒上的范德华力,与分离距离有关[8].Ingles[10]和Young[11]则认为粘着力还与静电力(其大小与土壤、水流中的离子特性有关)、水流的毛细作用等因素有关.

对于半径为r的可变形的表面光滑的球形颗粒,当它与光滑壁面接触时,其受到的粘着力约等于范德华力,计算如下[12]:

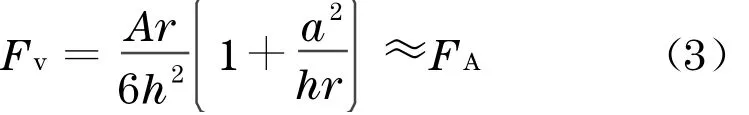
式中:Fv为范德华力, N;FA为粘着力, N;A为Hamaker 常数;h为分离距离,m;a为接触半径,m.

对于粒径较大的可变形的颗粒,其受到的粘着力可以通过经典Johnson-Kendall-Roberts(JKR)模型进行计算.根据该模型,粘着力可计算如下[13]:

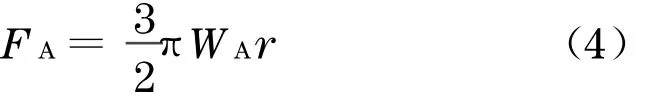
式中,WA为颗粒的表面能,J·m-2.

式中,hmin为最小分离距离,m.

对于研究可变形颗粒的壁面脱离运动,颗粒与壁面的接触半径是十分重要的参数.接触半径的确定可通过JK R 模型计算得到[14]:

式中,E为复合弹性模量,Pa,

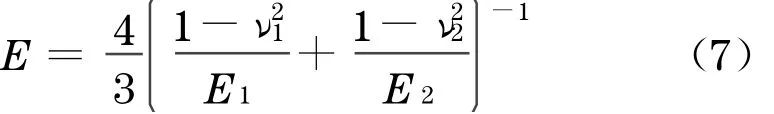
式中:ν1,ν2分别为材料1 和材料2 的泊松比;E1,E2分别为材料1 和材料2 的弹性模量,Pa.

1.3 自身的有效重度

颗粒自身受到重力作用,同时由于浸没在水中又受到水的浮力作用,因此颗粒自身的有效重度可以表示为

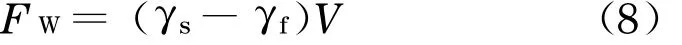
式中:FW为有效重度, N;γs为固体颗粒的重度,N ·m-3.

1.4 升力

如果在图2 中的假设孔隙管体中水流的真实速度有较大梯度,则在邻近壁面处会对颗粒产生升力作用,方向与重力方向相反.升力的计算公式可表示为[12]

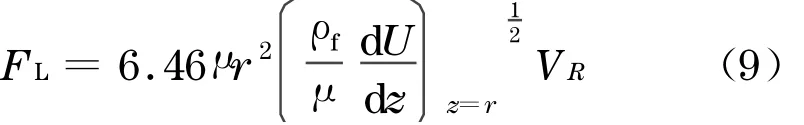
式中:ρf为水的密度,kg ·m-3;μ为水的动力粘性系数,N.s·m-2;U为平行于壁面的水流速度,m ·s-1;V R为颗粒与水流间的相对流速,m ·s-1;当颗粒没有脱离骨架时,VR=U.

对于含有粘性土的含水层,在考虑粘着力对颗粒脱离骨架影响时,由于升力的大小与粘着力相比,相差几个数量级,因此考虑了粘着力的情况下,通常可以忽略升力对颗粒的作用[8,15].对于粒径大于0.1 μm的颗粒也可以忽略升力对颗粒的作用[14].

2 颗粒脱离骨架运动方式分析

土体颗粒从含水层固体骨架脱离的过程受到多种因素的影响.如颗粒自身的物理性质(如几何形状、尺寸大小等);水流的物理和化学性质(如流速、温度、pH 值等)[16].本文仅从力学角度(颗粒和水流的物理性质方面)对脱离方式的影响进行分析.同时假设地下水温度不随时间变化,颗粒的形状考虑为完整球体, 与壁面接触时可发生变形, 接触面为圆形.

颗粒从固体骨架脱离方式主要有两种:①滑动脱离;②滚动脱离[17].下面对于颗粒脱离方式的讨论,主要考虑了拖曳力、粘着力、颗粒有效重度和升力四个作用力对颗粒的作用.对于无粘性土或粘性土含量极少的含水层,可以忽略粘着力对颗粒的影响.对于渗流速度较慢,具有较小速度梯度的地下水流,则可以忽略升力对颗粒的作用.

2.1 滑动脱离

对于滑动脱落,主要是考虑颗粒与壁面之间的摩擦作用,滑动脱离方式的平衡关系式如下:

式中:FH为颗粒受到的拖曳力,N;f为摩擦系数.当式(10)成立时,拖曳力克服颗粒与壁面的摩擦阻力,颗粒脱离固体骨架.

2.2 滚动脱离

滚动脱离主要是考虑动量的平衡,假设颗粒为半径为r的球体,与壁面接触处发生变形,接触面为圆形,接触半径为a.壁面的光滑程度对力矩平衡关系式的建立影响较大,需要把壁面分为光滑和粗糙两种情况进行讨论和分析.

对于光滑壁面,如图3 所示,颗粒绕B点滚动,发生滚动时需要满足关系式如下:

式中,D为绕B点滚动时拖曳力力臂,m .

对于粗糙壁面,如图4 所示,颗粒绕C 点滚动,发生滚动时需要满足关系式如下:

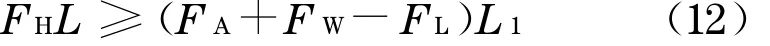
式中:L为绕接触点C处滚动时拖曳力力臂,m ;L1为绕接触点C处滚动时其他合力的力臂,m.

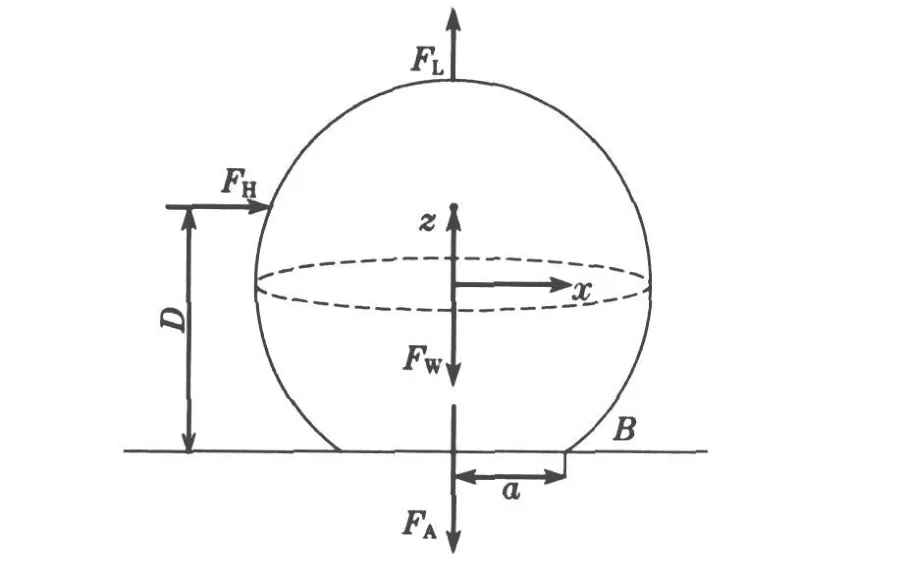
图3 颗粒在光滑表面发生滚动脱离示意图Fig.3 Schematic diagram of detachment mode of particle by rolling from smooth surface

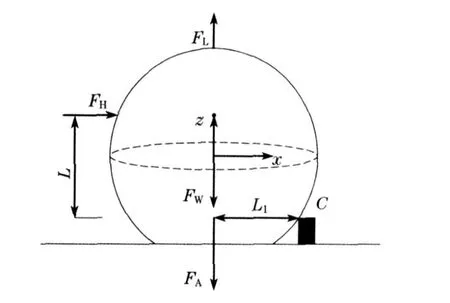
图4 颗粒在粗糙表面发生滚动脱离示意图Fig.4 Schematic diagram of detachment mode of particle by rolling from rough surface

很多文献指出通过实验研究发现,颗粒两种脱离方式中,以滚动脱离为主[13-14,18-19].

3 颗粒运动对地下水源热泵使用产生的影响

当土体颗粒通过上述两种脱离方式中的某种方式脱离含水层骨架时,根据颗粒脱离方式,选择相应的公式,计算出颗粒开始运动时的临界水力坡度.地下水动力学中指出渗流速度与水力坡度存在下述关系[20]:

各授予单位每年会将授予学位的博士论文名单上交至教育部。国家图书馆根据教育部年度博士论文授予名单对到馆博士论文进行核对，然而由于到馆的留学生博士论文封面信息常常与授予名单存在差异，使得到馆的留学生博士论文无法被检索到，或者被检索到的为错误的博士论文。

式中:Vs为渗流速度, m ·s-1;K为渗透系数,

m·s-1.

式中:Q为取水量,m3·h-1;A为热泵地下取水井的取水面积,m2.

通过式(13)可以求出当颗粒即将脱离骨架时的临界渗流速度;如果取水面积已知,则可以用式(14)计算出临界水流量.当进入热泵机组的水流量小于临界水流量时,颗粒不会脱离含水层骨架,不会发生井壁坍塌和井壁周围细颗粒介质重组等问题.因此在取水面积已知的条件下,可以依据临界水力坡度计算得到的临界水流量作为选取热泵机组的重要依据.

4 算例分析

运用上述理论对天津市第四系第Ⅱ淡水承压含水层进行计算分析.文献[21] 中指出该地区含水层厚度为26 ～48 m;渗透率范围为2.374 ～2.436 μm2;单井出水量为60 ～110 m3·h-1,可作为地下水源热泵用水.主要由细砂组成,细砂的粒径范围在0.075 ～0.25 mm 之间[22].为了分析含水层中粘性土对颗粒脱离的影响,假设把该含水层分为4 种类型:无粘性土、粘性土含量依次为10%, 20%和30%.对不同粒径颗粒的运动情况进行分析,脱离方式假设为最常见的滚动脱离,对该含水层颗粒脱离的临界水力坡度和临界渗流速度进行计算和分析,计算结果如图5 和图6 所示.从图5 和图6 中可以看出对于相同粒径的颗粒,含水层粘性土含量越高,临界水力坡度和临界渗流速度越大,比无粘性土的含水层大1 ～2 个数量级;随着粒径的增大,含粘性土含水层的颗粒脱离的临界水力坡度和临界渗流速度都逐渐减小,且变化幅度较大,而对于无粘性土的含水层则变化不大.因此含水层中的粘性土含量对颗粒脱离骨架有着重要的影响.

图7 为不同井径的完整井在取水量相同条件下的水力坡度计算结果分析,假设取水量为60 m3·h-1.可以看出当取水量达到60 m3·h-1时,4 种不同井径的取水井的水力坡度都远远大于颗粒脱离骨架的临界水力坡度,颗粒将会脱离含水层骨架.随着含水层厚度的增加及井径的增大, 水力坡度逐渐变小.

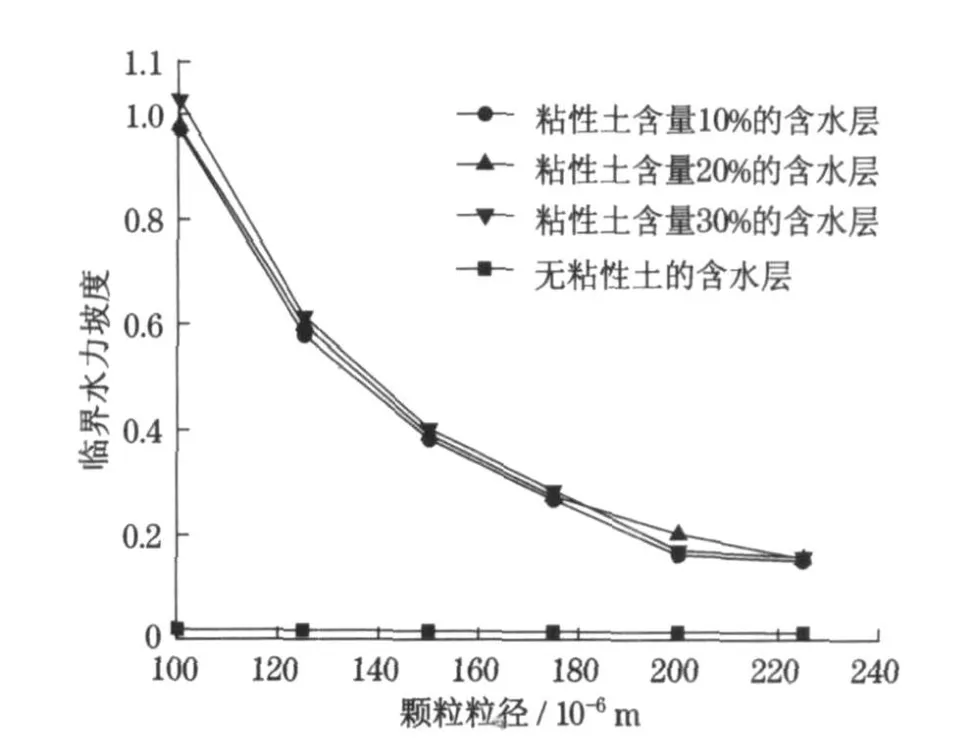
图5 不同粒径颗粒所组成含水层的临界水力坡度Fig.5 Critical hydraulic gradient value of aquifer composed by particles with different diameters

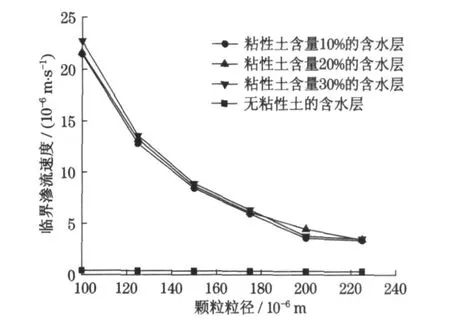
图6 不同粒径颗粒组成含水层的临界渗流速度Fig.6 Critical seepage velocity value of aquifer composed by particles with different diameters

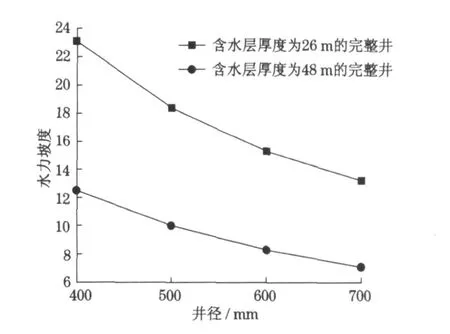
图7 不同井径的完整井在取水量相同条件下的水力坡度Fig.7 Hydraulic gradient value of fully penetrating well with different well diameters under the same discharge

因此为防止颗粒脱离含水层骨架情况的发生,地下水源热泵取水井应选取在厚度较大的含水层中(对于完整井),同时尽可能选取井径较大的取水井,增加取水面积,减小水力坡度;也可使用多口取水井同时取水的方法来满足热泵机组对水量的要求,减少单口取水井的取水量.

5 结论

(1)含水层中粘性土含量对颗粒脱离骨架有着重要的影响.粘性土的存在可以提高临界水力坡度和临界渗流速度,防止颗粒脱离固体骨架.

(2)如果地下水源热泵的取水井选用完整井,则取水井应选取在厚度较大的含水层中,同时尽可能增大取水井的井径.

(3)采用多口取水井同时取水的方法来解决单口取水井取水水量过大的问题,可以防止井壁坍塌和井壁周围细颗粒介质重组等问题的发生.

[ 1] 杨清.关于水源热泵水源问题的探讨[ J] .工程建设与设计,2004(6):5.YANG Qing.Study on w ater source of WSH P[ J] .Engineering Construction and Design,2004(6):5.

[ 2] 武晓峰,唐杰.地下水人工回灌与再利用[ J] .工程勘察, 1998(4):37.WU Xiaofeng, TANG Jie.Artificial recharge and reuse of g roundwater[ J] .Engineering Investigation, 1998(4):37.

[ 3] 李守德,徐红娟, 田军,等.均质土坝管涌发展过程的渗流场空间性状研究[ J] .岩土力学,2005(12):2001.LI Shoude,XU Hongjuan, TIAN Jun, et al.Researches on 3D seepage fields of soil dam under piping erosion[ J] .Rock and Soil Mechanics, 2005(12):2001.

[ 4] 周健,姚志雄,张刚.基于散体介质理论的砂土管涌机制研究[ J] .岩土力学与工程学报,2008(4):749.ZH OU Jian, YAO Zhixiong, ZH ANG Gang.Research on piping mechanism in sandy soils based on discrete element theory [ J] .Chinese Journal of Rock Mechanics and E ngineering,2008(4):749.

[ 5] Sterpi D.Effects of the erosion and transport of fine particles due to seepage flow [ J] .International Journal of Geom echanics,2003(3):111.

[ 6] 徐东强.土力学[ M] .北京:中国建材工业出版社, 2006.89-90.XU Dongqiang.Soil mechanics[ M] .Beijing:Chinese Building Materials Industry Press,2006.89-90.

[ 7] Simon A, Collison A J C.Pore-w ater pressure effects on the detachment of cohesive stream beds:seepage forces and matric suction[ J] .Earth Surface Processes and Landforms, 2001(26):1421.

[ 8] Sharm a M M,Chamous H ,Sarma S R.Factors controlling the hydrodynamic detachm ent of particles from surfaces[ J] .Journal of C olloid and Interface Science,1992(1):121.

[ 9] Reddi L N, Bonala M V S.C ritical shear stress and its relationship with cohesion for sand-kaolinite mixtures[ J] .Canadian Geotechnical Journal,1997(2):26.

[ 10] Ingles O G.Bonding forces in soils, part3 A theory of tensile strength for stabilized and naturally coherent soils[ C] ∥Proceeding s of the 1st Conference of the Australian Road Research Board.Vermont South:Australian Road Research Board Press,1962:1025-1047.

[ 11] Young R N,Sethi A J, Ludw ig H P.Interparticle action and rheology of dispersive clays[ J] .Journal of the Geotechnical Engineering Division ASCE,1979(105):1193.

[ 12] Burdick G M, Berman B S, Beaudoin S P.Hydrodynamic particle removal from surfaces[ J] .T hin Solid Films,2005(1-2):116.

[ 13] Ahmadi G.G UO Shiguang,ZH ANG Xinyu.Particle adhesion and detachm ent in turbulent flow s including capillary forces[ J] .Particulates Science and T echnology,2007(1):59.

[ 14] Soltani M, Ahmadi G.On particle adhesion and removal mechanisms in turbulent flow s[ J] .Journal of Adhesion Science and Technology,1994(7):763.

[ 15] Ziskind G, Fichman M, Gutfinger C.Adhesion moment model for estimating particle detachment from a surface[ J] .Journal of Aerosol Science,1997(28):623.

[ 16] Khilar K C.Water sensitivity of sandstones[ J] .Society of Petroleum Engineers Journal,1983(23):55.

[ 17] H ubbe M A.Theory of detachment of colloidal particles from flat surfaces exposed to flow[ J] .Colloids and Surfaces, 1984(12):151.

[ 18] Yiantsios S G, Karabelas A J.Detachm ent of spherical microparticles adhering on flat surfaces by hydrodynamic forces[ J] .Journal of Colloid and Interface Science, 1995(12):74.

[ 19] Das S K, Schechter R S, Sharma M M.Role of surface roughness and contact deformation on the hydrodynamic detachment of particles from surfaces[ J] .Journal of Colloid and Interface Science,1994(1):63.

[ 20] 李俊亭.地下水动力学[ M] .北京:地质出版社,1987.14-15.LI Junting.Groundw ater dynamics[ M] .Beijing:Geology Press,1987.14-15.

[ 21] 高莹君,孙振.天津市区第四系地下水资源分析[ J] .资源节约与环保,2006(1):43.GAO Yingjun, SUN Zhen.Resource analy sis of quaternary groundw ater in tianjin [ J ] . Resources Saving and Environmental Protection,2006(1):43.

[ 22] 方云,林彤,谭松林.土力学[ M] .武汉:中国地质大学出版社,2003.6-10.FANG Yun, LIN Tong, T AN Songlin.Soil mechanics[ M] .Wuhan:China University of Geosciences Press,2003.6-10.