基于二次感染的道路交通事故黑点建模*
盛玉刚 徐伟娟 过秀成
(南京林业大学汽车与交通工程学院1) 南京 210037) (东南大学数学系2) 南京市 210096)
(东南大学交通学院3) 南京 210096)
道路交通事故黑点(下简称事故黑点)是指受道路条件、交通条件、气候环境等因素的影响,在一个较长的时间段内(通常为1~3年),发生交通事故的数量和特征与其他正常点相比明显突出或者潜在安全隐患的点.事故黑点不仅严重降低了道路的服务质量,而且各事故黑点累计发生的事故次数占总事故次数的比例也很高,对道路的整体安全水平影响很大[1].以往对事故黑点的研究,多注重人的心理选择行为及安全道路理念[2-5],本文通过引入医学中对二次感染问题[6]的研究方法,探讨事故黑点的形成机理.
1 问题描述
道路交通事故主要成因构成如图1所示,由单因素造成的事故占总事故数的比例分别为:人的因素65.4%、道路因素5.6%、车辆因素1.6%;由双因素引发的交通事故占总事故数的比例分别为:由人的因素和道路因素共同作用引起的交通事故占35.4%,由人的因素与车辆因素引发的事故占4.3%,由道路因素与车辆因素引发的事故占3.6%;由3因素(道路因素、人的因素、车辆因素)共同作用引发的交通事故占总数的2.1%;除人车路因素外,还有其他事故成因(如天气、自然灾害、管理等),在多因素中,凡是涉及到道路因素、人的因素、车辆因素的事故分别占总数的35.9%,95.0%,9.8%.
可以看出,虽然由道路原因单独作用引起的交通事故所占比例不高(5.6%),但由于道路原因直接和间接导致的交通事故所占比例很高(35.9%).同理,人的因素也如此.
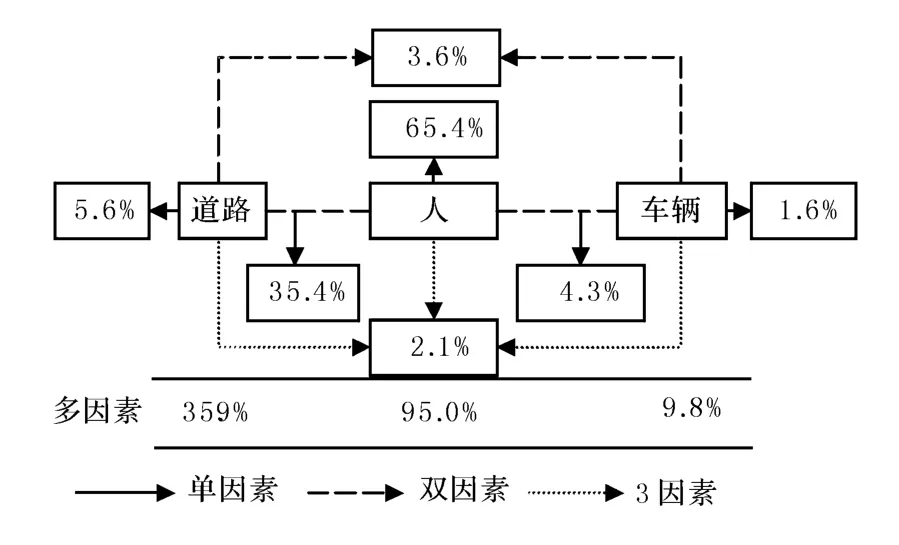
图1 公路交通事故成因比重
道路交通系统由机动车及驾驶员子系统、非机动车及行人子系统、道路子系统、环境子系统4个子系统构成(图2).机动车及驾驶人是一个密不可分的整体,故可以将车辆和驾驶人看成一个整体来进行研究,下简称人车体.

图2 道路交通系统示意图
道路子系统属于基础设施,是交通安全的一项重要因素.环境子系统包括交通运行状况、交通标志标线以及沿线社会环境等能影响人车体驾驶行为的信息变化状况.非机动车及行人子系统具有慢行交通的特性,具有一定稳定性,为方便研究,将其并入环境子系统考虑.综述之,道路交通系统可进一步简化为人车体子系统、道路子系统和环境子系统3个子系统构成(见图3).
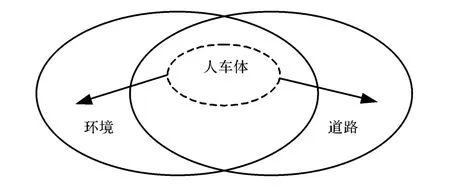
图3 道路交通系统简化图
2 事故黑点形成机理分析
文中假设一起事故是由于1~2个影响因素引发的,人车体受影响因素的感染引发事故的过程可简化为图4所示4个过程:(1)过程1,人车体未受任何因素影响时,其在路上正常运行,称其为原生质体;(2)过程2,人车体受因素1的影响,成为一次感染体,但感染程度未达到发生事故的水平,人车体继续前行;(3)过程3,人车体在影响因素1的作用下(一次感染体),继续前行,人车体处于隐患状态;(4)过程4,人车体继续受因素2的影响,由一次感染体转化为二次感染体,感染程度达到发生事故的水平,交通事故发生.
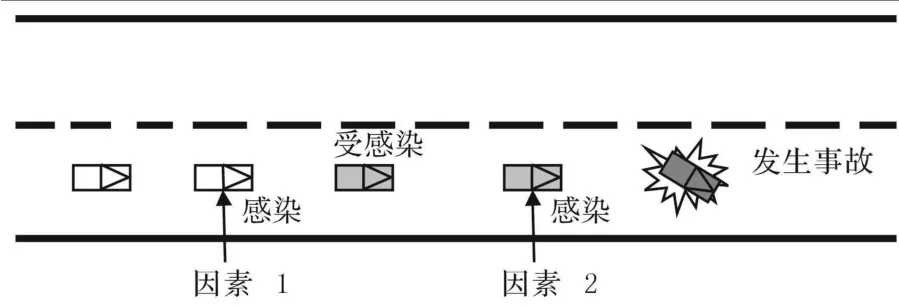
图4 车辆受感染引发事故过程图
实际情况并不一定如此,可能会产生如下几种情形(见表1).
当沿线没有影响因素或影响因素的感染强度为弱的情况下,人车体正常通过路段,如情形1,2,4;当其中有一个或以上因素感染强度为强时,即发生交通事故,如情形3,7,8;如果沿线2个影响因素的感染强度均为弱,则可能发生两种情况,若影响因素在空间上分布较靠近,则易引发交通事故(情形6),若相隔较远,则第一个影响因素的感染会在一段时间内自愈,人车体不会发生事故(情形5).可知,事故的发生必须有影响因素的存在,如果没有影响因素,则可认为人车体会一直正常行驶在道路上;即使存在影响因素,还必须看该影响因素是否具有感染性,以及感染的强度.
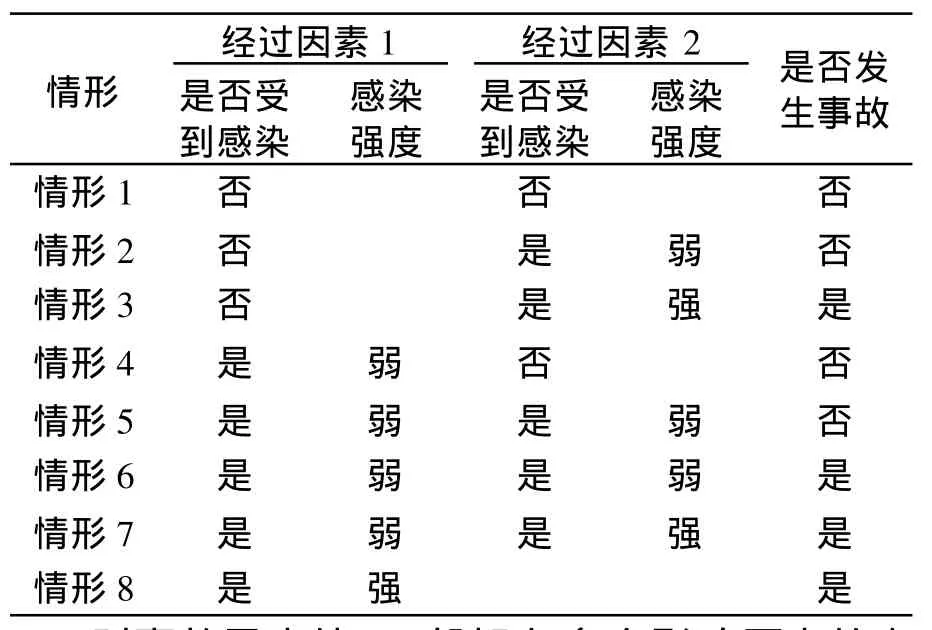
表1 人车体受双因素感染情况列表
对事故黑点处,一般都有多个影响因素的存在,其引发交通事故必须具备如下条件:(1)存在影响因素,如果公路沿线没有影响因素,则认为人车体会正常行驶,无交通事故的发生;(2)影响因素能具有感染性,人车体遇到影响因素,可能被感染,也可能不被感染,如果不被感染,则无交通事故的发生;(3)感染必须达到一定程度,人车体即使受感染,但如果感染程度不深,也不会发生交通事故,而且随着人车体继续前行,所受感染会自愈;(4)影响因素的必须具有一定的集聚度,人车体如果受第一个影响因素的影响,但未达到发生交通事故的程度,如果间隔距离足够长,在到达第二个影响因素时,人车体会自愈,将第一次受感染的影响恢复到人车体的初始状态.因此,影响因素的间隔距离不能太远,否则无法形成事故黑点.
3 模型的建立
3.1 双因素模型
引发交通事故的因素可能同时存在2种甚至更多种.首先讨论由1~2个影响因素引发事故黑点的形成机理模型,根据事故黑点形成机理,一条公路某点或路段通过的人车体,按是否受影响因素的感染进行二次划分,可以抽象成表2.

表2 二次感染划分表
式中 :~Z=Bγ22+Bγ21(n I p-q-Bγ11)-1Bγ12;α可取5%.
根据以上不等式,反解即可得到θ2(即危险率δ)的置信区间.下式为一种求近似置信区间上下限的
表中:p11为2次都受感染的概率;p12为第一次受感染而第二次未受感染的概率;p21为第一次未受感染而第二次受感染的概率,没有初次感染就不存在二次感染,故 p21≡0;p22为第一次未受感染而第二次也未受感染的概率;p1为初次感染的概率,p1=p11+p12;p2为未受感染的概率,p2=p21+p22.

式中:p1为受第一个因素或2个因素影响后发生事故的概率;p11/p1为在受第一个因素影响后接着受第二个因素影响的条件概率;δ为2个概率的比值,称其为危险率.则当<p1时,危险率 δ<1,人车体未受影响因素的感染,不发生交通事故,该点段不是事故黑点;当 p11/p1≥p1时,危险率δ≥1,人车体受1~2个影响因素的感染后发生交通事故,该点段容易形成事故黑点.危险率越大,越容易形成事故黑点.
3.2 模型求解
如果p11,p12,p22参数已知,则模型易求解.但是通常无法得到此三参数的精确概率值,当样本量足够大时,可用它们的极大似然估计值来代替,从而可以得到危险率δ的置信区间.如果令p1=θ1,δ=θ2,可以得到
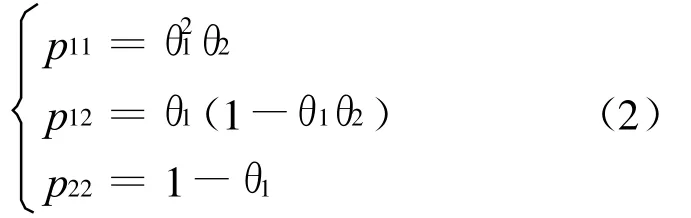
以上模型都可看作非线性多项分布模型,可以采用几何方法求解参数置信域的一般公式,并应用于危险率的区间估计.由于在列联表中参数服从多项分布,所以在2×2表中,(p11,p12,p22)服从3项分布,通过3项分布的性质来求解子集参数θ2的统计性质[7-8],即由双因素引发的交通事故危险率的置信区间.
由多项式的性质可得到,关于水平1-α的子集参数θ2的近似置信区间可表示为
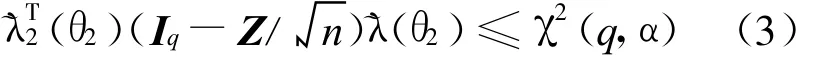
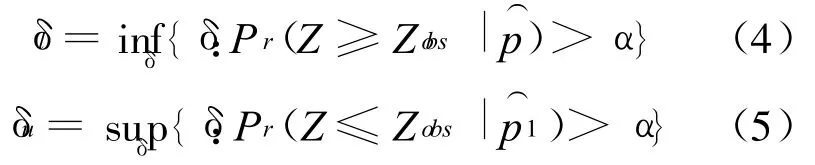
区间(δl,δu)是 δ的水平为(1-α)的置信区间,可基于MATLAB开发子集参数置信区间的求解程序,实现对近似解的求解.
3.3 扩展多因素模型
人车体受3个影响因素、4个因素……等多因素感染机理的研究,可根据双因素影响机理的研究思路进行适当扩展.
当人车体受因素1、因素2的感染后,仍未达到发生交通事故的程度,继续前行.可将因素1、因素2联合作用看成因素1′,因素3看成因素2′.
简化后的感染模型,其关于水平1-α的子集参数θ2的近似置信区间可表示为
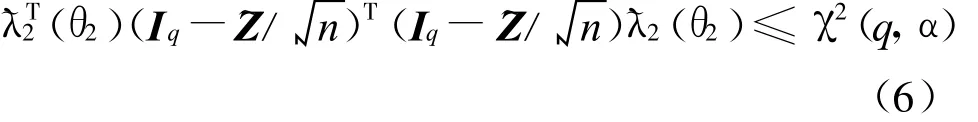
式中 :~Z=Bγ22+Bγ21(n Ip-q-Bγ11)-1;α可取5%.
4 模型验证
为验证模型的适用性,筛选某一级公路主要事故黑点数据进行计算.表3为事故黑点统计表,根据历年事故统计数据及交通量数据,可得到p11,p12,p22的极大似然估计,计算值列于表3.利用MATLAB开发子集参数置信区间的求解程序,计算得出95%水平下δ的置信区间(δL,δu)如表3所列.
计算结果表明,危险率δ的置信区间下限基本上都高于1,模型对事故黑点的验证率较高.
5 结 论
1)根据影响因素与交通事故的关系,道路交通系统可进一步简化为由人车体子系统、道路子系统和环境子系统3个子系统构成的动态系统.
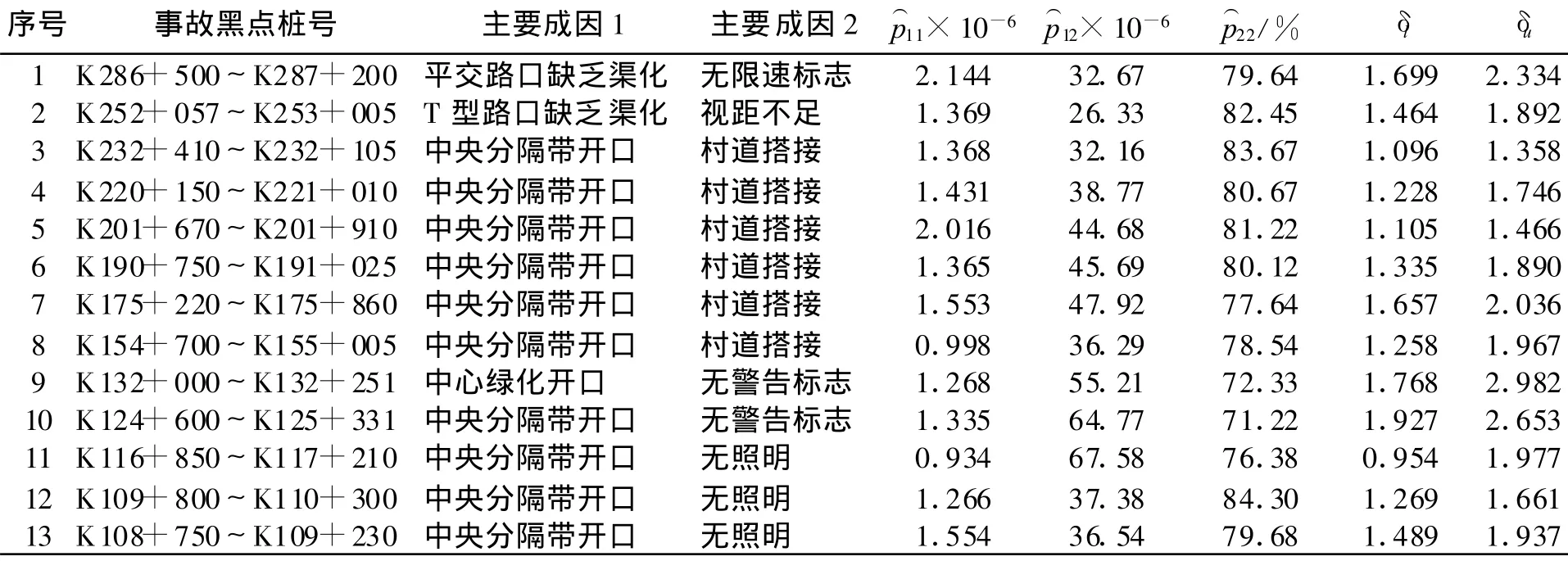
表3 黑点统计表
2)事故黑点形成必须具备如下条件:存在影响因素、影响因素具有感染性、感染必须达到一定程度、影响因素的必须具有一定的集聚度.
3)事故黑点模型的求解在一定样本容量下,可将参数的极大似然估计值代替精确值,通过三项分布的性质来求解子集参数的近似置信区间.通过实例计算,验证了事故黑点模型的适用性.
[1]过秀成.道路交通安全学[M].南京:东南大学出版社,2004.
[2]胡江碧.事故多发地点形成机理及分析方法的研究[D].北京:北京工业大学交通研究中心,2004.
[3]李 斌,王 猛,汪 林,等.驾驶时间对营运驾驶员驾驶能力影响的试验研究[J].公路交通科技,2007,24(5):113-114.
[4]刘兴旺.道路交通事故发生机理与成因分析[D].哈尔滨:哈尔滨工业大学交通科学与工程学院,2005.
[5]牟军敏,邹早建,黄立文,等.水上交通事故模式的研究[J].武汉理工大学学报:交通科学与工程版,2005,29(3):489-490.
[6]LuiK J.Confidence intervals of the sim ple difference betw een the p roportions of a primary in fec tion and a secondary infection,given the primary infection[J].Biometrical Journal,2000,42(2):59-69.
[7]Berger S,Boos D D.P-valuemaxim ized over a con fidence set for the nuisance parameter.Journal of the American[J]Statistical Association,1994,89(2):1012-1016
[8]Pam ilton D C.Con fidence regions for parameter subsets in non linear regression[J].Biometrika,1986,73(1):57-64.

