大地测量Stokes边值问题的自然边界元解法*
唐元义 许厚泽 胡清峰 骆有隆
(湖北大学数学与计算机科学学院1) 武汉 430062)
(中国科学院测量与地球物理研究动力大地测量学重点实验室2) 武汉 430077)
(武汉理工大学管理学院3) 武汉 430070)
0 引 言
大地测量边值问题,一般利用Stokes公式,采用有限差分法或快速富氏变换(FFT)等来计算.唐元义等研究了用自然边界元法对大地测量的第二、第三边值问题进行求解[1-2],所采用的方法是由Neumann外问题得大地测量边值问题的自然积分方程,然后再离散求解.
现在根据自然边界元的基本思想,直接得到大地测量Stokes边值问题的自然积分方程,再用离散化技术进行求解.
1 Stokes边值问题
地球重力场可以用地球重力位来表达.通常把重力位W分成2部分:正常重力位U和扰动位T.正常重力位U可用4个大地测量基本参数来确定,是一个已知函数;扰动位 T是一个待求的微量函数.大地测量边值问题,就是利用观测数据给定边值条件,来推求扰动位及外部重力场的问题.
假定通过重力归算,已经把大地水准面外的地球质量去掉,并假定正常椭球中心与地球质心重合,旋转角速度等于地球自转角速度,则大地水准面外空间的扰动位满足Lap lace微分方程,即Δt=0,而且在无穷远处是正则的.
已知观测量是重力异常 Δg,求扰动位的问题,就是大地测量Stokes边值问题
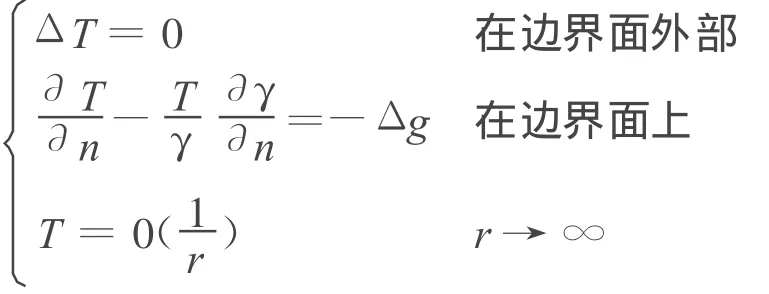
上面第一式为扰动位 T的Lap lace方程;第二式为物理大地测量学的基本微分关系.式中γ为正常重力,左端是T和 的线性组合(n为边界面的外法线方向),右端的重力异常是已知的,边界面一般为大地水准面.
用球面近似代替大地水准面,即所谓的球近似,这使 T具有扁率级的误差.物理大地测量Stokes边值问题,在球近似的情形下可归结为如下的Robin问题
式中:S为球面,SC球面外部.
2 扰动位的Poisson积分式表示
由于扰动位 T=W-U是谐函数,可以用Poisson积分式表示为
式中 :T(r,θ,λ)为计算点的扰动位 ;T(R,θ′,λ′)为球面r=R上的扰动位;ψ为球面上计算点(θ,λ)与积分流动点(θ′,λ′)的球心角
扰动位 T(r,θ,λ)也写成谐函数级数形式
式中:Tl(θ,λ)为 l阶的 Lap lace面谐函数
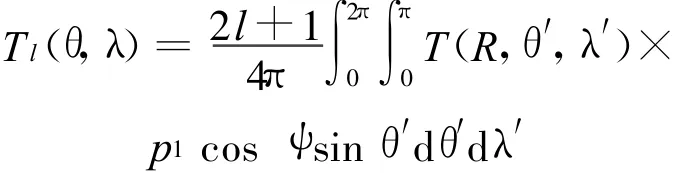
将式(1)对r求导,得谐函数的径向导数
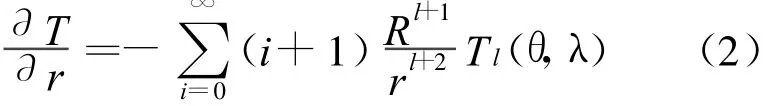
在地球外,边值条件为
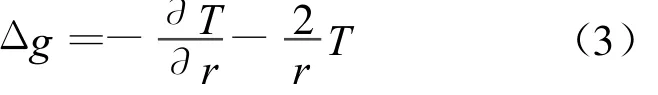
将式(2)代入式(3)得
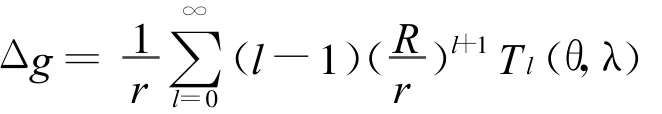
当r=R时,就变为
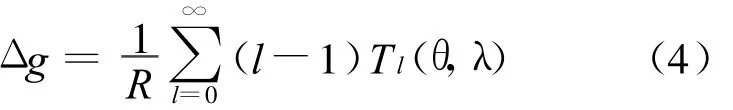
即为重力异常的球谐表达式.
3 边值问题的自然边界元法
在式(4)两边同时乘以γ¯T,∀γ¯T∈T(S)(γ为迹算子,T(S)由自然积分算子K导出的迹空间[3]),再作内积,也仍相等,即有

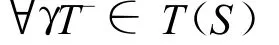
式中:(· ,·)为内积(球面积分)如下式
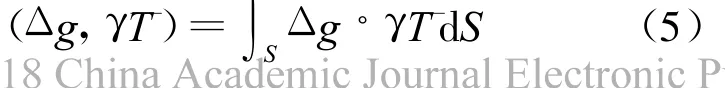
则有
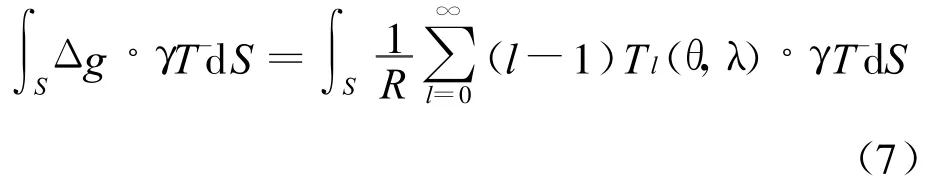
从式(7)可以看出,用离散化技术求解对自然积分方程,就可求出球面S(大地水准面)上的扰动位 T了(扰动位 T含在Tl(θ,λ)中).
4 边值问题的自然边界元求解
对球面S作有限元剖分,Sh(S)为相应于该剖分、由适当选取的基函数张成的H1/2(S)的线性子空间,得到自然积分方程的近似变分问题[4].
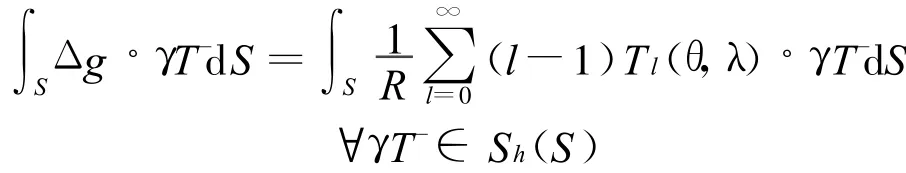
设

由此构造球面S上的分片双线性插值基函数Φ0(θ,φ)=L0(θ),Φ1(θ,φ)=LN1(θ),Φsj(θ,φ)=Ls(θ)Mj(φ),s=1,2,…,N1-1;j=1,2,…,N2.则 Sh(S)=span{Φ0(θ,φ),Φ1(θ,φ),Φsj(θ,φ),s=1,2,…,N1-1,j=1,2,…,N2}⊂H1(S)
设 Th0(θ,φ)=T0Φ0(θ,φ)+T1Φ1(θ,φ)取S上的基函数,则由自然积分方程可得线性方程组

5 结 束 语
大地测量Stokes公式是传统的经典公式,利用有限差分法或FFT,早为大地测量学家们所公认和采用.而大地测量边值问题的自然边界元法,用的是边界元法,在理论上是完全正确的.
当然,在实际应用中,即在作数值计算的时,实际效果如何,是否具有比传统的有限差分法更具有优势,或与有限差分法结合起来,或者与有限元法结合,取长补短,等等许多问题,将是需要进一步深入研究的课题.
[1]唐元义.GPS-边值问题的自然边界元解法[J].武汉理工大学学报:交通科学与工程版,2007,31(2):266-269.
[2]唐元义,许厚泽.物理大地测量边值问题的自然边界元解法[J].武汉理工大学学报:交通科学与工程版,2008,32(1):146-148.
[3]余德浩.自然边界元方法的数学理论[M].北京:科学出版社,1993.
[4]邬吉明,余德浩.三维调和问题的自然积分方程及其数值解[J].计算数学,1998,20(4):419-430.

