关于《工程数学》与《自动控制原理》课程知识之衔接
陈俊英
(集美大学工程技术学院 福建 厦门 361021)
关于《工程数学》与《自动控制原理》课程知识之衔接
陈俊英
(集美大学工程技术学院 福建 厦门 361021)
《工程数学》是《自动控制原理》课程的数学基础,联系紧密,但实际教学中,这两门课往往不能很好地衔接,给《自动控制原理》课程的讲授造成了不小的困难,影响了教学效果。为此,可以在学习《自动控制原理》课程知识开始之前,就拉氏变换与傅立叶变换的知识作一个有针对性的复习,使两门课程知识融会贯通。
工程数学;自动控制原理;衔接;拉氏变换;傅立叶变换
《自动控制原理》是机械类专业的一门必修课,是一门理论性和实践性都很强的课程,其所有知识点的讲授都以积分变换即以拉氏变换与反变换、傅立叶变换与反变换为基础。
一般情况下,由数学系的教师来讲授《工程数学》积分变换的相关课程,而单纯的数学理论讲授很难做到将《工程数学》课程知识与《自动控制原理》课程进行联系。而《自动控制原理》的任课教师则认为该部分内容已经讲过,也不会再详尽述及,更不会细心去理顺基本概念,当学生进入《自动控制原理》课程学习的时候,难以接受突然出现的拉氏变换应用,以致认为该课程内容很高深,挫伤了学习的自信心。因此,在讲授《自动控制原理》课程之前,笔者先理顺拉氏变换、反变换,傅立叶变换、反变换之间的关系,而在讲授该知识点之前,更是先安排关于常规方法解微分方程的知识,以强化学生对各学科之间逻辑关系的认识。
时域分析知识准备
《自动控制原理》课程是以数学建模为基础的,而时域模型又体现为微分方程,所以微分方程的求解是基本功。用一般方法求解较繁琐,不同的微分方程首先要区分方程的形式,然后根据不同的形式,采用不同的解法。
(一)一阶微分方程
1.变量可分离类型,形如y'sin x=ylny用分离变量的方法求解。
(二)二阶微分方程
1.可降阶的二阶微分方程,形如:
形如y''=f(x,y')(缺y),令p=y'求解。
形如y''=f(y,y')(缺x),令p=y'
2.二阶常系数线性齐次方程,形如
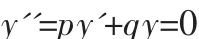
通解求法:先求特征方程r2+pr+q=0的特征根。特征根不同,通解不同。
3.二阶常系数线性非齐次方程
通解求法同二阶常系数线性齐次方程,而特解依方程右式形式的不同而不同。
以上内容在讲授时,只须述及方程形式和解题方法,这是复习过渡性质的内容,无须详述,主要是让学生了解用常规方法解微分方程非常繁琐。 而自动控制系统的数学建模、传递函数的求取需要大量求解微分方程,因此降低求解微分方程难度意义重大,此时即可引入拉氏变换简化微分方程求解过程的知识。这样,学生对于拉氏变换的意义有了生动的理解,知识脉络清晰,更具逻辑性。
(三)应用拉氏变换解线性微分方程
具体步骤如下:(1)对线性微分方程中每一项进行拉氏变换,使微分方程变为代数方程。(2)解代数方程,得到有关变量的拉氏变换表达式。(3)用拉氏反变换得到微分方程的时域解。
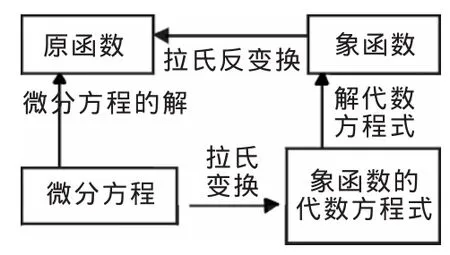
图1 求解过程示意图
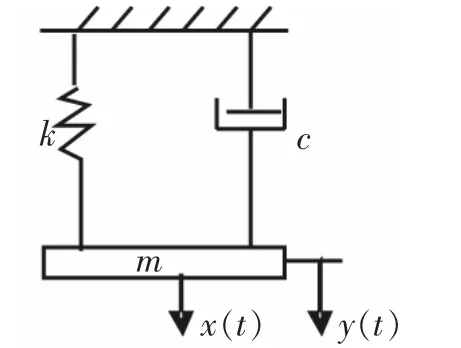
图2 二阶模型图
典型实例:设一弹簧上端固定,下端悬挂一质量为m的物体,取其平衡位置为坐标原点O,轴铅直向下,物体沿Y轴运动,开始时(t=0),物体的初始位移为Y0,初始速度为v0,求物体的运动规律。
解:数学建模:因阻力与速度成正比,故阻力为
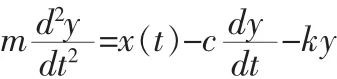
(已知yt=0=0,y't=0,x(t)=k·1(t))
而弹簧力与位移成正比,为-ky,若系统所受外力为x(t),则根据牛顿第二定律有:
解:设L[y(t)]=Y(s)
对方程两边取拉氏变换,得
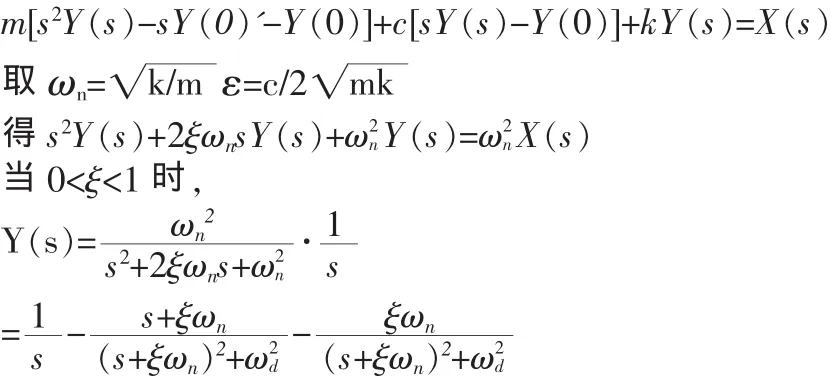
可见通过拉氏变换与反变换,可以将复杂的求解微分方程的问题转化成代数运算过程,大大简化了微分方程的求解过程。
频域分析知识准备
时域分析虽然比较直观,但如果不借助计算机,分析高阶系统会非常繁琐。而由于机械振动与频率特性有着密切的关系,所以频域法是工程上广为采用的分析和综合系统的间接方法。频域处理不仅简洁、计算工作量小,而且更能显示信号或系统的组成特性。但是测试者所观察到的总是信号的时间历程,要在频域进行处理和分析就必须先做时-频域变换。计算机技术实现时-频域变换的DFT和FFT算法已为广大工程人员所熟悉,有现成的程序可以调用,而频域分析的基础是傅立叶变换,故首先则应建立起傅立叶变换的物理意义。
(一)傅立叶级数
一般周期信号可以利用傅立叶级数展开成无穷多个不同频率的谐波信号的线性叠加。


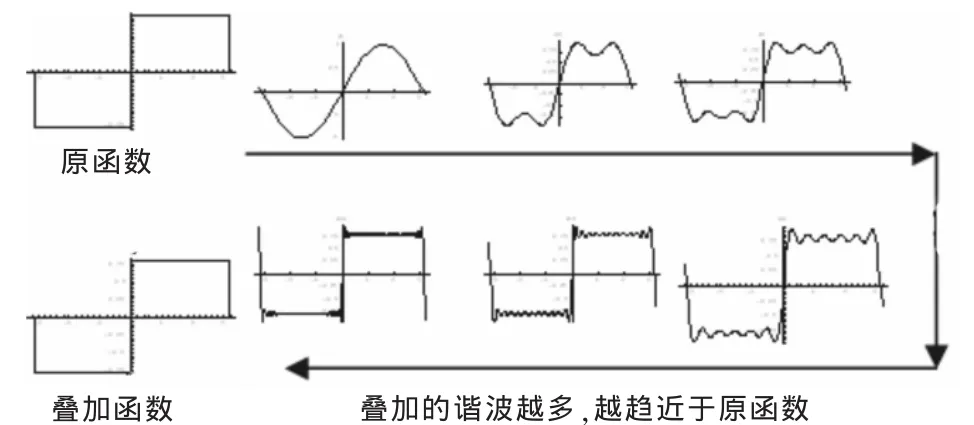
图3 谐波叠加现象示意图
图3可形象地表达出不同频率的谐波信号的线性叠加现象,从而使学生建立起频谱的概念。
(二)傅立叶变换
非周期信号x(t)傅立叶变换:

傅立叶反变换为:
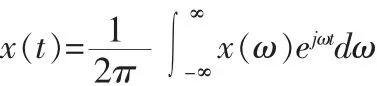
x(ω)是非周期函数的频谱函数,是连续的,而周期函数的频谱是离散的。
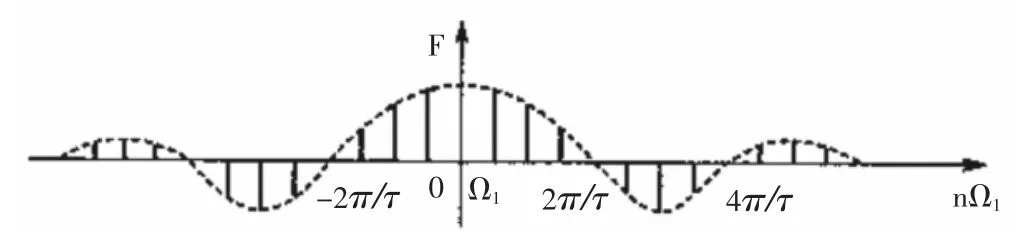
图4 周期矩形函数的离散频谱图
应特别说明单位阶跃信号的频谱,由于单位阶跃信号是时域分析的典型信号,了解单位阶跃信号的频谱,更有助于建立起时域分析与频域分析的关系(如图5)。
拉氏变换与傅立叶变换的关系
对于傅立叶变换,理解物理意义比进行具体运算更有意义,因为拉氏变换算子S=σ+jω,即当σ=0时,FL(S)=FF(jω)在严格的理论推导下成立。这为教材中频域分析傅立叶变换以拉氏变换为过渡打下理论基础。系统模型间的关系(如图6)。
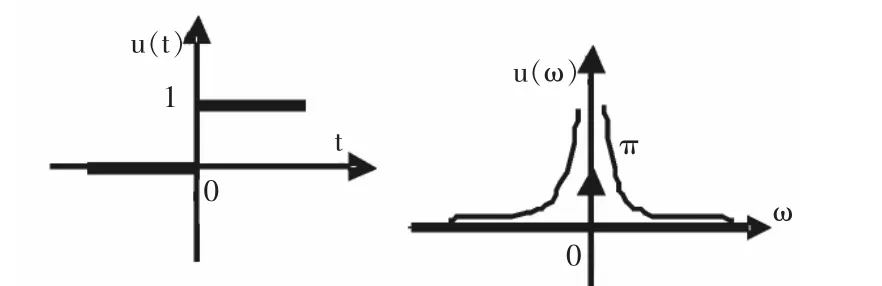
图5 单位阶跃函数频谱图
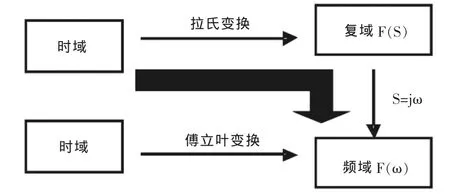
图6 拉氏变换与傅立叶变换关系示意图
在开始《自动控制原理》课程之前,复习拉氏变换,使学生理解采用拉氏变换的真正原因,而傅立叶变换的介绍则加强了学生对频域物理意义的理解,从而为学习频域分析的幅频相频特性打下基础。通过对拉氏变换与傅立叶变换之间关系的介绍,可以为频域分析知识讲授起到铺垫作用,较好地改善教学效果。
[1]曾光宇,等.现代传感器技术与应用基础[M].北京:北京理工大学出版社,2007:14-15.
[2]严普强,等.动态测试信号处理中时-频域变换算法的讨论[J].振动、测试与诊断,2003,(7):120-124.
[3]褚言正,等.关于信号单边拉普拉斯变换与傅里叶变换关系的研究[J],重庆科技学院学报(自然科学版),2006,(7):114-115.
陈俊英(1974—),女,工学硕士,集美大学工程技术学院讲师,主要研究方向为传感器与测控技术。
(本文责任编辑:张维佳)
G642
A
1672-5727(2010)S0-0063-02

