钢管轧制的非线性耦合振动分析

杨琳琳 郝润元 陈建勋

(太原科技大学重型机械教育部工程中心/山西省现代轧制工程技术研究中心，山西030024)

钢管轧制的非线性耦合振动分析

杨琳琳 郝润元 陈建勋

(太原科技大学重型机械教育部工程中心/山西省现代轧制工程技术研究中心，山西030024)

基于接触力学和非线性振动理论，考虑了钢管轧制过程的非线性刚度和阻尼因素，建立了钢管的两自由度非线性耦合振动模型，分析了激励频率和压下量等变化参数对钢管振动的影响。结果表明：随着激励频率的增加，钢管轧制中会出现混沌状态，破坏轧制的稳定性；合理的压下量可以减小钢管振动速度，提高钢管表面质量。

钢管；轧制；压下量；非线性振动；数值分析

轧钢工业中的轧管机组普遍存在自激振动问题，它不但影响轧制设备的运行性能，还诱发钢管产生振动，严重影响钢管的质量和精度。Mohammed[1]建立了四自由度的线性直串垂振系统，分析了参数变化对产品质量的影响。Nessier[2]研究了辊系的弯曲振动特性以及平整机的倍频程颤振。Yarita[3]提出了两自由度线性垂振系统，通过分析辊系间刚度的简谐波动，研究了线性参激共振现象。Hu[4，5]建立了单自由度和多自由度轧机振动模型，研究了轧机系统的稳定性，对连轧过程进行了仿真。以上研究都取得了一定的成果，并从不同角度分析了振动机理，但是没有考虑钢管在轧制过程中的振动问题。本文将轧机自振为激励，以接触动力学为基础，应用非线性振动相关理论，重点分析研究钢管在变刚度变阻尼情况下两自由度非线性耦合振动特性。

1 钢管空间非线性接触赫兹力

轧辊和轧件之间的弹性接触符合Hertz分布。设法将集中力p作用在弹性半空间表面，另一点(x，y)产生的法向位移由Boussinesq解得出[6]

(1)

在载荷Q作用下，两物体由于弹性变形而形成接触区域S。S内的接触应力应满足

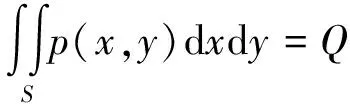
(2)

则变形协调方程为

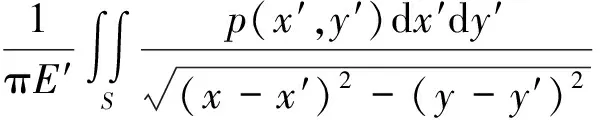
=u-Ax2-By2

(3)

u为原点，相对于接触平面位移，S内压力分布的半椭球函数为

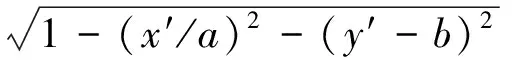
(4)

p0=3Q/2πab

(5)

可得

(6)

(7)

(8)

(9)

(10)

(11)

(12)

式中，v1和v2分别是两物体的泊松比；E1和E2分别是两物体的弹性模量；∑ρ是曲率和函数；K(e)是第一类完全椭圆积分；E(e)是第二类完全椭圆积分。

则非线性接触赫兹力为：

Q=ku3/2

(13)

(14)

2 钢管非线性振动数学模型

钢管在轧制过程中的耦合振动模型如图1所示。

图1 钢管耦合振动示意图Figure 1 Schematic drawing of steel pipe coupled vibration

2.1 垂直方向的振动模型

由于轧机机组在运行阶段产生自激振动，在垂直方向将给钢管一个时变的激励F0cosωt，ω是轧机机组自身的固有角频率。其简化模型如图2所示。

根据拉格朗日定理，其动力微分方程为

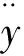
(15)

式中，m是钢管质量；k是接触刚度，其值由式(14)得到；c是接触阻尼，c=ηk；η值可查阅文献[7]；δ是压下量。

2.2 水平方向的振动模型

钢管水平方向振动的模型如图3所示。因为钢管在轧制过程中的结构刚度和阻尼时刻发生变化，故此系统的非线性刚度项和非线性阻尼项采用前后张力的刚度和阻尼的duffing振子组合形式(kq+khx2)和van der pol振子组合形式(-cq+chx2)分别定义。振动简化模型如图4所示。

轧制力的水平分力Fx=Fsinα，α是轧机的咬入角。

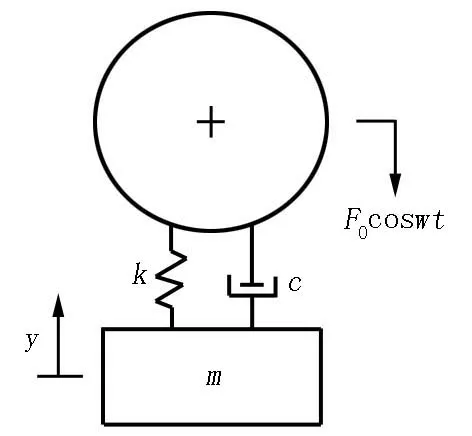
图2 垂直方向简化振动模型Figure 2 Simplified vibration model in vertical direction

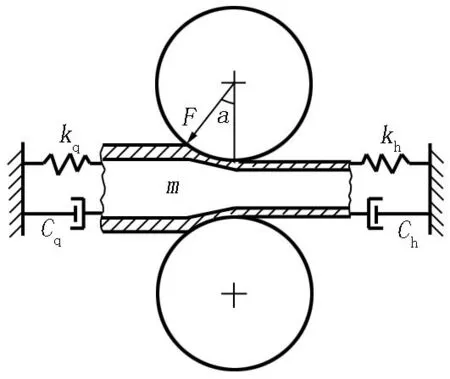
图3 钢管水平振动模型Figure 3 Horizontal vibration model of steel pipe

图4 水平方向简化模型示意图Figure 4 Schematic drawing of simplified vibration model in horizontal direction

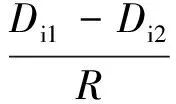
(16)

式中，Di1是机架i减径前钢管的直径；R是轧辊半径。摩擦力Ff=μF。

则其振动微分方程为

(17)

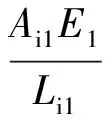
2.3 非线性耦合振动

钢管两自由度的耦合振动方程为

(18)

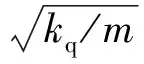
从而将振动方程化为

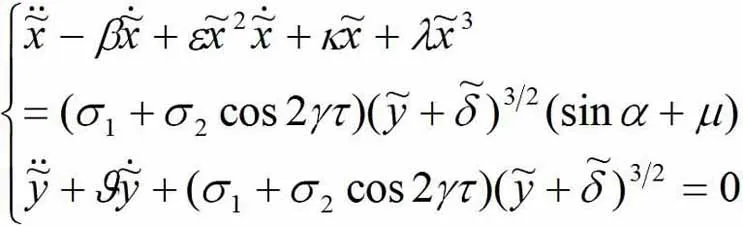
(19)

3 实例计算与分析

某重工厂生产的ZGTY-426四辊斜轧管机，其主要参数如下：轧辊转速90 r/min；轧辊最小直径850 mm；轧辊材料为合金钢，泊松比0.27，弹性模量210 GPa；毛管直径242 mm，壁厚19 mm，长度7 m；荒管直径232 mm，壁厚12 mm，长度9 m；钢管质量3.2 t，钢管材料为碳钢，泊松比0.24，弹性模量202 GPa，最大轧制力2 000 kN。

将以上参数代入式(19)，由于方程(19)的强非线性，运用Runge-Kutta-Felhberg算法对其求解。

3.1 不同激励下轧制系统的动力学特性

考虑到轧机机组对钢管轧制过程的影响，以频率比 为参数，图5给出了频率比 在0至2之间的分岔图。从图5中可以看出，轧制中频率比为0.74时，振幅突然增大。图6分别给出了频率比在0.1、0.2、0.72、0.8和1.5时的Poincare截面图，用来分析钢管轧制的全部过程。当频率比为0.1时，系统处在拟周期运行状态。随着频率比的增加， 在0.2时系统进入多周期运行状态，即稳定状态。频率比 在0.72～0.76阶段，系统开始失稳，进入混沌状态，随后钢管便逐步趋向于稳定。因此，在实际操作过程中，合理控制轧机参数，有效地避开此频率段，可以使整个机组更加稳定的运行。

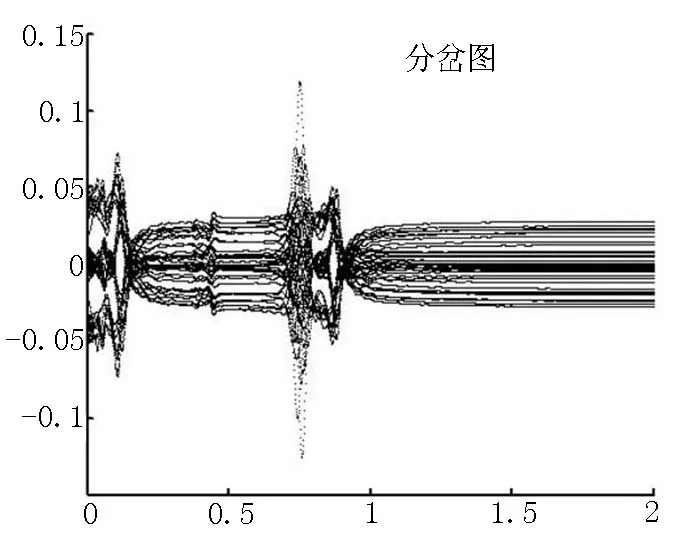
图5 系统随频率比变化的分岔图Figure 5 Splitting diagram of the variety of system along frequency ratio

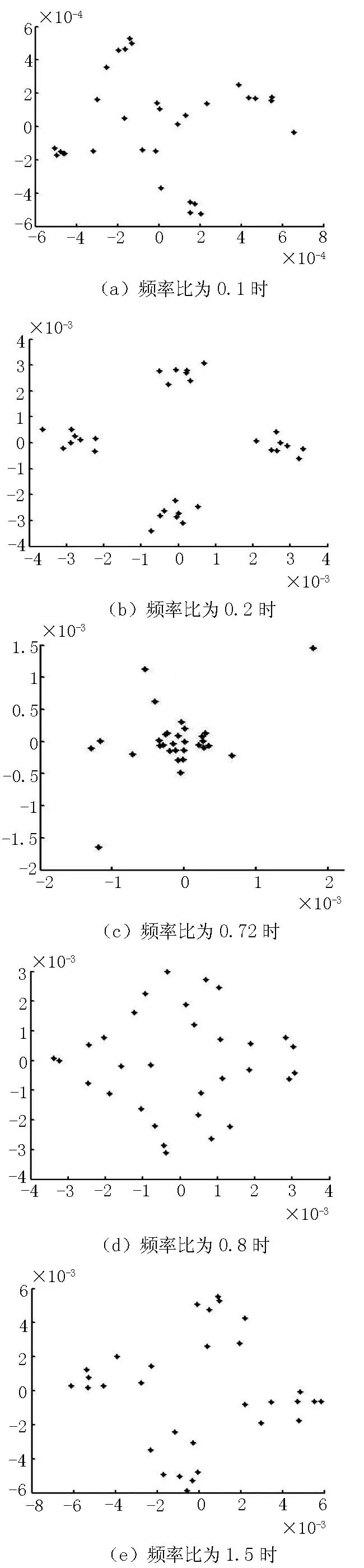
图6 不同频率比时的Poincare截面图Figure 6 Poincare sectional view at different frequency ratio

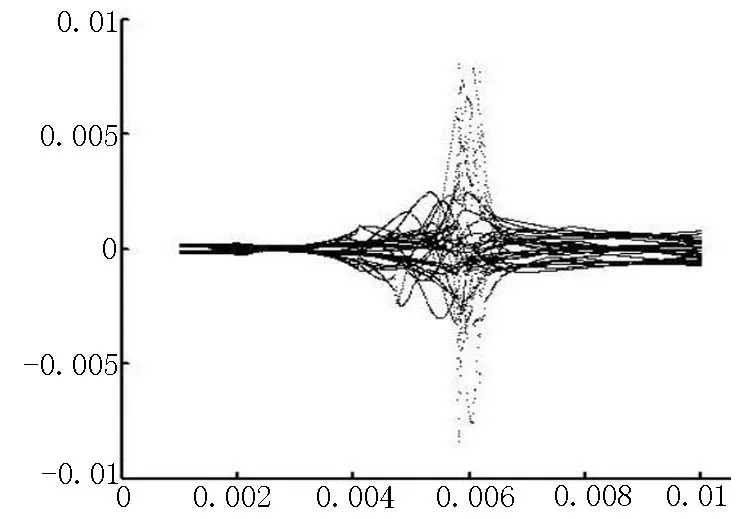
图7 水平速度随压下量的变化图Figure 7 The variety of horizontal velocity along screw down amount

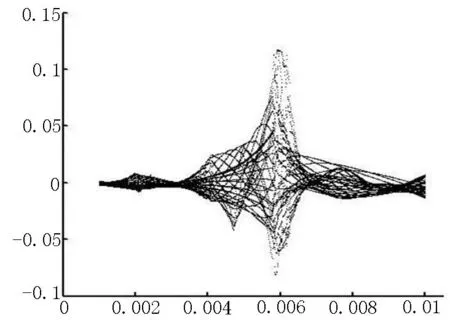
图8 水垂直速度随压下量的变化图Figure 8 The variety of water vertical velocity along screw down amount

3.2 压下量对轧制钢管的影响

压下量在轧制过程中是逐渐变化的。为了定量分析，将压下量作为控制参数。图7和图8是压下量从1 mm～10 mm时钢管水平和垂直方向的速度变化图。从图7可看出，当压下量在5 mm～7 mm阶段，钢管振动速度开始加大，并在6 mm处达到最大，振动剧烈。从图8可看出，在垂直方向，压下量在3 mm、7 mm和9 mm时振动最小。因此，根据轧机和钢管的参数综合考虑，可以选取最优压下量，使钢管在两个方向上的振动最小，这样有利于提高钢管的轧制精度。

4 结论

本文从钢管振动的角度出发，引入接触力学和非线性动力学理论，建立了钢管在变刚度变阻尼情况下的两自由度非线性振动模型，分析了频率比对轧机机组运行稳定性的影响和压下量与钢管表面质量的关系。研究表明：

(1)机组在运行过程中有一阶段处于混沌状态，因此适当的控制频率比，可使机组避开此频率段，稳定运行。

(2)压下量与钢管振动速度存在明确的关系，根据实际参数选择合理的压下量，可以减小钢管表面粗糙度和波纹度，提高钢管的质量和精度。

[1] Mohammad A,Younes M,Shahtout R.A parameters design approach to improve product quality and equipment performance in hot rolling[J].Journal of Materials Processing Technology,2006，171(1)：83-92.

[2] Nessier G L,Cory J Fr.Cause solution of fifth octave backup roll chatter on 4-h cold mils and temper mills.AISE Year Book,1989(12)：33-37.

[3] Yarita I,Furukawa K,Seino Y.An analysis of chattering in cold rolling of ultrathin gauge steel st rip[J].Transactions ISU,1979，19(1)：1-10.

[4] Hu P H,Ehmann K F.A dynamic model of the rolling process:Part Ⅰ[J].Int J Mach Tools Manuf,2000，40(1)：1-19.

[5] Hu P H,Ehmann K F.A dynamic model of the rolling process:Part Ⅱ[J].Int J Mach Tools Manuf,2000，40(1)：21-31.

[6] 钱长伟，叶开源.弹性力学[M].北京：科学出版社，1980.

[7] 张威刚，高尚晗，龙新华，等.机床主轴滚动轴承系统非线性动力学分析[J].振动与冲击，2008，27(9)：72-75.

The Analysis for Non-linear Coupled Vibration of Steel Pipe Rolling

YangLinlin,HaoRunyuan,ChenJianxun

According to the contact mechanics and non-linear vibration theory, and taking the non-linear rigidity and damping factor in the process of steel pipe rolling into account, non-linear coupled vibration model with two freedom degrees is established and the influence of variation parameters such as pump frequency and screw down amount to the steel pipe vibration is analyzed. The result shows that chaos situation will occur during steel pipe rolling to break the stability of rolling along pump frequency is increased, and reasonable screw down amount can reduce the steel pipe vibration velocity to improve the surface quality of steel pipe.

steel pipe; rolling; screw down amount; non-linear vibration; value analysis

TG335

A

2010—05—25

杨琳琳(1985—)，女，硕士研究生，研究方向：复杂轧机微尺度结构动态研究，高精度管材矫直工艺参数分析。

郝润元(1960—)，男，教授，研究方向：无缝钢管成套设备研究，钢管矫直机矫直理论及结构研究。

陈建勋(1966—)，男，高级工程师，研究方向：无缝钢管生产工艺研究，钢管矫直工艺优化设计。

编辑 杜青泉

工业品质量信誉论坛开幕国机等央企发起承诺

9月2日，首届中国工业产品质量信誉论坛在北京开幕。中共中央政治局委员、国务院副总理张德江出席开幕式并致词。他强调，要深入贯彻落实科学发展观，坚定不移地把加强工业产品质量工作作为加快转变工业发展方式、促进工业由大变强的关键举措，着力落实企业质量主体责任，着力加快质量技术进步，着力加强质量诚信体系建设，着力严格质量监督管理，努力把工业产品质量提高到一个新水平。

包括中国航天科工集团公司、中国石油化工集团公司、海尔集团等在内的156家发起单位向全社会作出承诺，以“诚实守信为荣，以见利忘义为耻”，让诚信经营成为全体员工的共有理念和行为准则，坚决抵制以次充好、虚假宣传等侵害消费者权益的违法行为，自觉接受消费者、政府和社会监督，支持行业自律管理，将履行质量承诺、追求质量诚信作为企业发展不懈追求的目标。

(摘自中国二重纪检监察网2010-09-10)