基于积分法的铝合金厚板深度残余应力分析

廖凯 ，吴运新，龚海

(1. 中南大学 机电工程学院，湖南 长沙，410083；2. 桂林电子科技大学 教学实践部，广西 桂林 541003)

测试金属表面残余应力的方法有多种，应用广泛的有钻孔法、X线衍射法[1−2]等。在对金属内部残余应力进行测试的方法中，无损检测技术有中子衍射方法，但这种方法所要求的实验硬件条件在国内还无法实现，因此，在金属内部特别是在板材内部，残余应力的检测均为有损检测，其中层削法和裂纹柔度法最常用[3−4]。1931 年 Stäblein 等采用层剥法对直梁内应力进行了测定[5]，并推导了应用于方板上的数学模型。而裂纹柔度法是一种较新被研究和应用的测试方法。一些研究者结合有限元法简化了应力因子的计算，用常规方法检测残余应力，如 Prime等[6−9]利用有限元法计算裂纹柔度系数，推广了裂纹柔度测试级数，并认为所有这类应力有损检测方法的数学模型都可以用第一类 Volterra积分来描述并求解。国内王树宏等[10−13]运用上述求解方法对铝合金厚板全厚度残余应力进行了测试研究。在层削测试方法[11]的基础上采用一种具有离散法性质的计算方法，这种算法对复杂应力状况缺乏稳定的连续描述能力。为此，本文作者将线性积分形式在层削法和裂纹柔度法数学模型中的应用进行归纳和总结，分析这2种测试方法的建模过程和计算特点，并结合实验，对这2种测试方法的计算结果进行比较和分析。

1 积分法

由于机械加工和采用热处理工艺，铝合金材料不可避免地产生内部残余应力[14]。残余应力是一种产生于材料内部的自平衡弹性力，测试厚板残余应力的力学方法一般为：沿厚度方向，按一定增量步长(厚度)，通过机械方法剥除或破坏带有应力的厚度层，从而使相邻试件因力平衡状态的改变而变形，用测得的变形反求出剥除层应力。在测试中，由于是用某一点的应变衡量整个厚板的变形，样本的变形量与剥除层待求应力所依据的实体分离，测定并不在同一个区域或同一个点，因此，无法直接通过变形来反求应力。求解方法可用积分法。Schajer等[15]通过对有损测试方法研究后提出：第一类Volterra积分形式描述这种应力−应变的关系非常有效，即试件剥除后的变形量是剥除层应力与变形对应力敏感函数(核函数)在剥除厚度上的积分。这类求解方法称为积分法，该法用离散实验数据求解得到 1条连续变化的应力场分布曲线，其方程为：

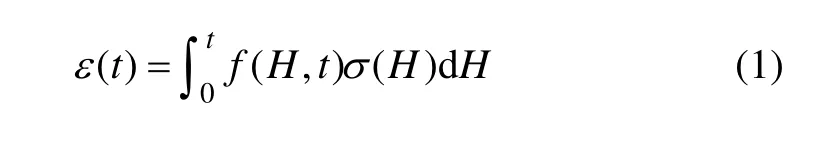
式中：t为剥除层厚度；σ(H)是板厚为H时的初始应力；ε(t)为实测应变；f(H,t)为变形对板厚H处应力的敏感函数即核函数。

1.1 层削法(Removal layer method)

由轧制−淬火厚板热应力形成的对称性特点可知，厚板应力为平面应力，为简化分析，设沿板材厚度z向的残余应力为0，且对称于厚度中性面，σz=0，σx= σx(z )， σy= σy(z)，1/2厚板切削过程示意图如图1所示。测量时，应变片贴于厚板中心处。

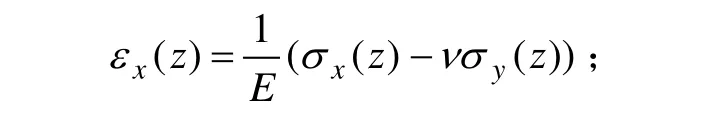
图1 试件层削法力学模型Fig.1 Mechanical model of removal layer method

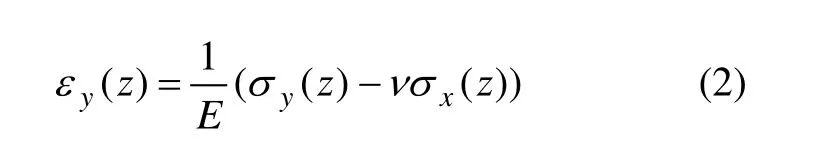
式中：ν为泊松比。以x向应变为例，残余应力分布力和力矩平衡条件为：

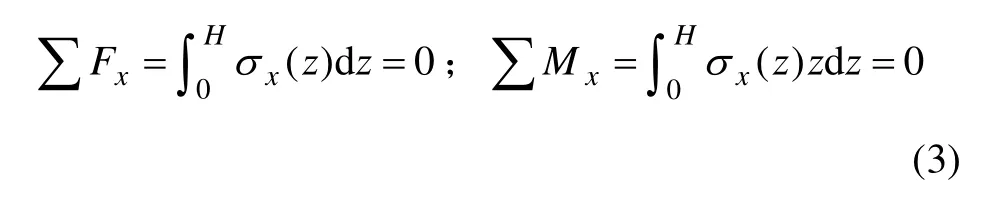
其中：H为板厚。在剥除层深度为t时，应力平衡条件改变，附加力和附加力矩产生的附加应力 σFx(t)和σMx(t )与初始应力 σx( z)叠加，构成新的平衡状态，满足：

由剥除层后附加力和附加弯矩产生变形的实测应变为：

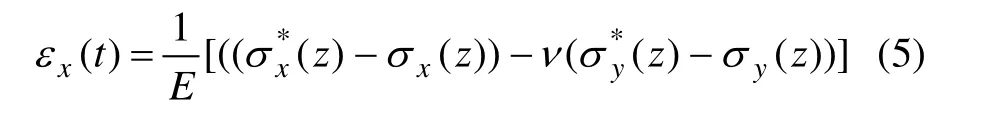
式中：E为弹性模量。则应力−应变积分形式为：

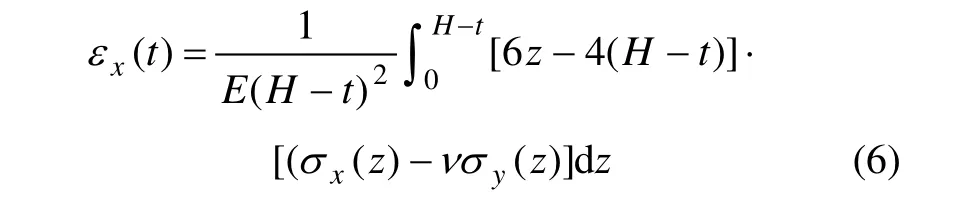
假设待求残余应力为多项式 P，求解出待定系数Ai和 Bi即可。

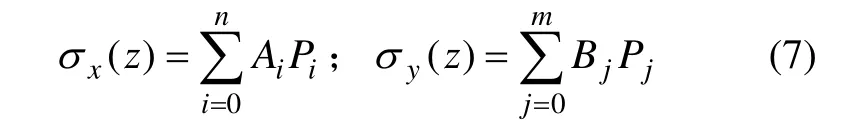
联立式(6)～(7)可以求解待定系数[16]。假设对式(6)～(7)都以相同阶次多项式近似，则

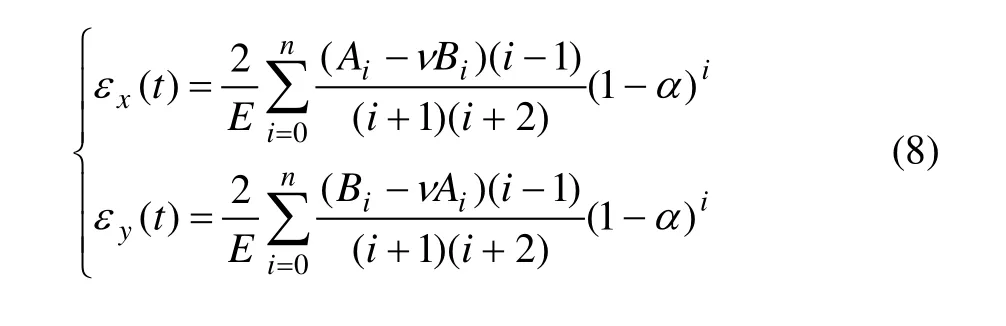
1.2 裂纹柔度法(Crack compliance method)

该法是在被测物表面引入1条逐渐深入的裂纹，使裂纹处残余应力释放，通过测量裂缝对面处的应变计算残余应力。测试力学方法如图2所示。由于该法既可测试表面应力，也可测试深度方向应力，因此，应变片可以根据需要在不同的地方布置，对深度应力的描述要求应变片贴在板的底面上且底面和裂纹的交点处。此点对残余正应力的响应最大，对残余剪切应力的响应为 0。而测试表面应力时，可将片贴在靠近裂纹的上表面处。

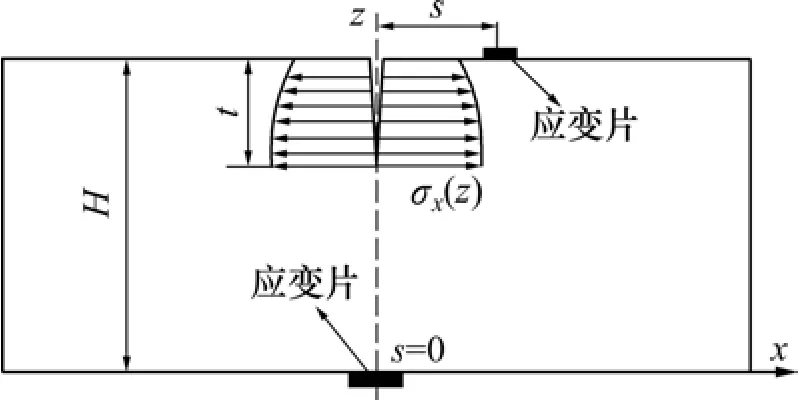
图2 试件裂纹柔度法力学模型Fig.2 Mechanical model of crack compliance method

试件内正应力 σx( z)在裂纹作用下，在距离裂纹s的应变片处产生水平位移u。假设在该位移处有一虚拟力 F，可作为沿宽度方向归一化处理的点载荷，则由裂纹产生的应变能Uε为：

其中：KI(t )和(t,s )为分别由正应力和虚拟力引起的Ⅰ型应力因子。运用卡氏定理，上表面断裂处水平位移为：

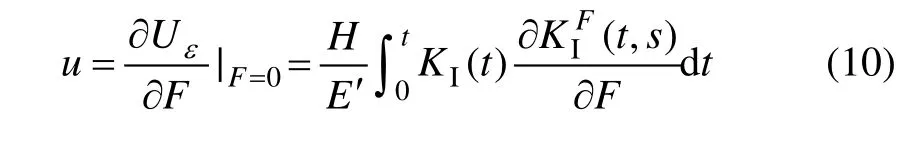
Cheng等[17]给出了求解Ⅰ型应力因子的方法，其中由虚拟点载荷F引起的正应力与位置函数 S(s, z)有关。当求裂纹正下方处的应变时，只需要将S(s, z)替换为S(s, H−z)，并令s=0即可。

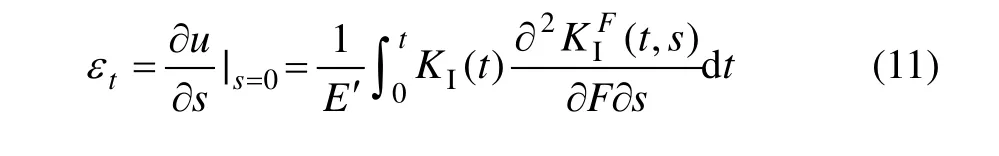
初始残余应力 σx( z)沿厚度方向应该是对称的且分布曲线光滑，因此，可以用多项式代替应力形式(如式(10))：

其中：Ci为裂纹柔度函数。可以结合有限元和矩阵法[8]确定柔度矩阵和待定系数。柔度矩阵中的元素是对于深度为tj的切口处，由假设的多项式函数Pi(x)所导致的应变 ε ( tj)。由于待定系数(多项式阶次+1)小于切割次数，因此，联立式(12)，运用LSF求解待定系数Ai。

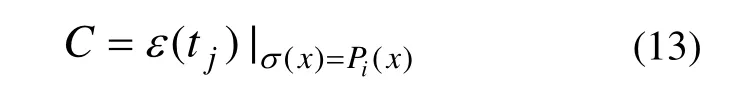
联立式(15)和(16)求解得：

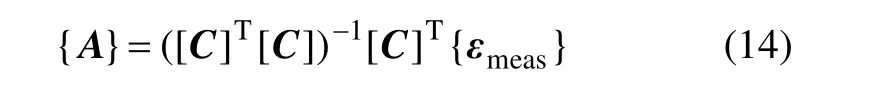
式中：ε( tj)为有限元模拟中每一次切深在切口对面处产生的应变；{εmeas}为实测应变。

2 实验与分析

从理论建模和实验结果分析可知：由于获得变形的方法以及运用的理论基础存在差异，采用层削法和裂纹柔度法测试残余应力并非都可以得到满意的结果，测试结果存在差异。

2.1 实验方法

为验证上述2种测试方法在不同应力厚板测试中的测试效果及差异性，实验选用7075轧制厚板，热处理工艺为：固溶480 ℃×2 h，20 ℃水淬+24 h自然时效。测试分2组：

(1) 非均匀应力场测试。用长×宽×高为 160 mm×160 mm×32 mm的厚板2块，直接于20 ℃水浴淬火。由于受淬火边缘效应的影响，待测厚板在同一深度上平面应力分布不均匀程度和应力较大。

(2) 均匀应力场测试。先将长×宽×高为 1 200 mm×220 mm×32 mm 的实验厚板用喷水(20 ℃)淬火，残余应力与前者相比较低；再从厚板中部截取长×宽×高为120 mm×120 mm×32 mm厚板2块，以保证应力在轧制方向和横向比较均匀。对每一组分别进行层削法和裂纹柔度测试实验，在层削法实验中，在LEADWELL V−60A数控加工中心进行铣削。为减小加工应力的影响，铣刀转速为1 000 r/min，进给速度为50 mm/min[18]。裂纹柔度法时，裂纹引入型号为DK系列线切割机，进给速度为3 mm/min，频率为85 Hz。

非均匀板由于受边缘和二维表面淬火影响，应力沿平面2个方向分布极不均匀，极易形成非均匀应力场，而均匀板由于取自大尺寸板心部，根据圣维南原理，应力沿平面2个方向分布较均匀。为了便于比较，在不影响实验真实性前提下，根据假设，对实验数据沿板厚进行对称化处理。

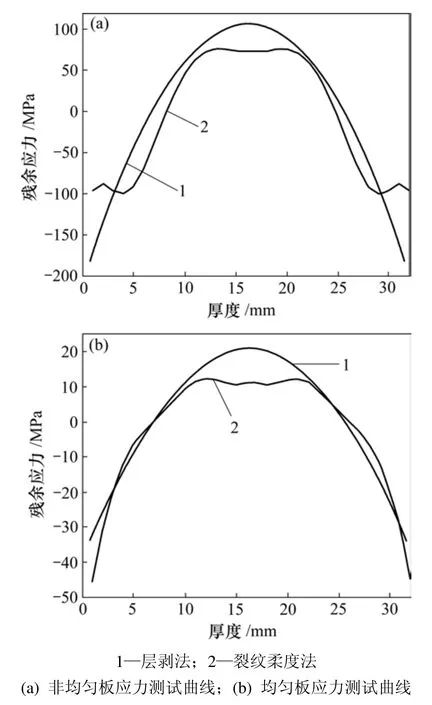
图3 层削法与裂纹柔度法测试结果对比Fig.3 Comparison of solution between removal layer method and crack compliance method

2.2 结果分析

在力学建模的假设条件中，残余应力沿厚度方向变化，在其他2个方向均匀不变。但无论是均匀板还是非均匀板，平面应力在各个方向上分布都不可能均匀。例如在某一层上，在轧制方向和横向上应力不均匀程度不同。图3(a)所示为非均匀应力厚板在2种测试方法下得到的应力分布曲线，其中2条曲线显示了相同的演变规律，即淬火厚板常见的“外压内拉”分布。比较图3(a)中的2条曲线可以发现：它们的不同之处体现在应力不同，用层削法计算的应力为−180～98 MPa，其范围明显大于裂纹柔度法计算所得的−102～80 MPa；而相同的特征则反映在两者计算结果于厚板中心区域所反映出来的应力梯度变化都很小，这也反映了不同积分计算方法具有相似性。图3(b)所示为均匀应力厚板在 2种测试方法下的应力分布曲线，2条曲线吻合程度提高，说明在一定条件下，2种独立的力学测试方法都能描述厚板内应力，具有一定的互换性。

通过比较测试结果发现：在厚板表面和中心部位应力计算结果存在差异，这种差异可从计算方法和实验综合考虑。除了铣削加工应力远大于电火花加工应力而导致误差外，由于层削法是用若干点的应变平均值这个单一变量描述整个厚板变形程度和状态，而获得的却是剥除层内平均应力，这不可避免地使计算值与真实值偏离；而裂纹柔度法所得应力反映了裂纹处应力的平均值，断裂变形测试受不均匀变形的影响小，用测得的应变反映断裂程度较符合客观现象。因此，前者的实验测试误差大于后者。

此外，这2种方法的力学模型都是建立在忽略了材料各向异性特点、假设材料均匀连续的经典弹性和线弹性断裂力学基础上，与实际情况相比存在差异，这也给计算结果带来了误差。

在求解过程中，由于铣削次数远少于裂纹引入次数，求解线性方程借助最小二乘法处理的多项式系数的阶次就少，因此，表征应力曲线的准确度与后者相比较低，其抗干扰能力弱。

采用层削法时，1次切削深度为2 mm左右，求解结果是整个剥除层的平均应力，并不是某一确切位置上的应力；而采用裂纹柔度法时，虽然可以1次切深0.5～1.0 mm，但受表面复杂应力和板件自重的影响，靠近表面的应力都会出现较大波动，需要进行数学处理。因此，采用这2种方法得到的应力分布曲线都不能准确地反映厚板表面应力，甚至与X线表面应力测试所得的应力不同，而用于描述厚板沿厚度应力场分布非常有效。这是积分法力学测试的特点之一。

3 结论

(1) 积分法适用于厚板残余应力测试方法的数学计算，如层削法、裂纹柔度法、钻孔法等。通常这类通过力学破坏而获得变形，从而反求应力的计算方法，几乎都可以运用积分法建立变形与应力之间的数学关系。

(2) 层削法可用来描述厚板沿厚度方向的平均残余应力分布，属于应力全部释放型测试方法；裂纹柔度法则用于描述裂纹处沿厚度方向平均残余应力分布，属于应力局部释放型测试方法，这对于描述厚板内部残余应力特征有重要的意义。对内部应力均匀的试件，这2种测试方法所得结果很相近，然而，对不均匀试件的测试结果存在差别。

(3) 虽然厚板深度残余应力的测试和计算方法还需要不断完善、发展，但在现有实验条件下，采用以上 2种测试方法从不同角度对厚板内应力场进行描述，仍然是目前评估厚板残余应力的有效方法。

[1]陈冷, 张清辉, 毛卫民. 残余应力及其分布的 X 射线二维衍射分析与计算[J]. 材料热处理学报, 2006, 27(1): 120−124.CHEN Leng, ZHANG Qing-hui, MAO Wei-min. Analysis and computation of residual stresses mapping based on X-ray two-dimensional diffraction[J]. Transactions of Materials and Heat Treatment, 2006, 27(1): 120−124.

[2]谢列卫, 刘勇, 潘海华. 铝合金材料残余应力测试的钻孔法研究[J]. 机械强度, 1995, 17(1): 31−34.XIE Li-wei, LIU Yong, PAN Hai-hua. Study for measuring residual stresses on al-alloy by the hole-drilling method[J].Journal of Mechanical Strength, 1995, 17(1): 31−34.

[3]王秋成, 柯映林, 邢鸿燕. 板类构件内部残余应力测试技术研究[J]. 浙江大学学报: 工学版, 2005, 3(3): 381−384.WANG Qiu-cheng, KE Ying-lin, XING Hong-yan. Study on measurement method of interior stress distributions in engineering rolled-plates[J]. Journal of Zhejiang University:Engineering Science, 2005, 3(3): 381−384.

[4]王秋成, 柯映林. 航空高强度铝合金残余应力的抑制与消除[J]. 航空材料学报, 2002, 22(3): 59−62.WANG Qiu-cheng, KE Ying-lin. Control and relief of residual stresses in high-strength aluminium alloy parts for aerospace industry[J]. Journal of Aeronautical Materials, 2002, 22(3):59−62.

[5]米谷茂. 残余应力的产生和对策[M]. 北京: 机械工业出版社,1983: 1−5.MI Gu-mao. Formation and countermeasure of residual stress[M]. Beijing: Machinery Industry Press, 1983: 1−5.

[6]Prime M B, Hill M R. Residual stress, stress relief, and inhomogeneity in aluminum plate[J]. Scripta Materialia, 2000,46(1): 77−82.

[7]Prime M B. Residual stress measurement by successive extension of a slot: The crack compliance method[J]. Applied Mechanics Reviews, 1999, 52(2): 75−96.

[8]Prime M B. Experimental procedure for crack compliance(slitting) measurements of residual stress[EB/OL].http://www.lanl.gov/residual/.

[9]Prime M B, Hill M R. Uncertainty analysis, model error, and order selection for series-expanded, residual-stress inverse solutions[J]. Journal of Engineering Materials and Technology,2006, 128(2): 175−185.

[10]王树宏, 左敦稳, 润长生. LY12, B95和7075铝合金预拉伸厚板内部残余应力分布特征评估与分析[J]. 材料工程, 2004(10):32−35.WANG Shu-hong, ZUO Dun-wen, RUN Chang-sheng.Evaluation and comparison of residual stress in thick prestretched aluminum plate of LY12, B95 and 7075[J]. Material Engineering, 2004(10): 32−35.

[11]张旦闻, 刘宏昭, 刘平. 裂纹柔度法在 7075铝合金板残余应力检测中的应用[J]. 材料热处理学报, 2006, 27(2): 126−131.ZHANG Dan-wen, LIU Hong-zhao, LIU Ping. Evaluation of residual stresses in 7075 aluminum alloy plate using crack compliance method[J]. Transactions of Materials and Heat Treatment, 2006, 27(2): 126−131.

[12]唐志涛, 刘战强, 艾兴, 等. 基于裂纹柔度法的铝合金预拉伸板内部残余应力测试[J]. 中国有色金属学报, 2007, 17(9):1404−1409.TANG Zhi-tao, LIU Zhan-qiang, AI Xing, et al. Measuring residual stresses depth profile in pre-stretched aluminum alloy plate using crack compliance method[J]. The Chinese Journal of Nonferrous Metals, 2007, 17(9): 1404−1409.

[13]张旦闻, 刘宏昭, 陆军攀, 等. 转动结构在精密铜合金板带残余应力检测中的应用和分析[J]. 中国有色金属学报, 2006,16(1): 130−135.ZHANG Dan-wen, LIU Hong-zhao, LU Jun-pan, et al.Applications and analyses of rotating structure in residual stress measurement on high accurate copper-alloy strip[J]. The Chinese Journal of Nonferrous Metals, 2006, 16(1): 130−135.

[14]王昌臻, 潘清林, 何运斌, 等. 2124 铝合金热轧厚板的热处理制度[J]. 中南大学学报: 自然科学版, 2007, 38(3): 386−393.WANG Chang-zhen, PAN Qing-lin, HE Yun-bin, et al. Heat treatment of thick hot-rolled plate of 2124 alloy[J]. Journal of Central South University: Science and Technology, 2007, 38(3):386−393.

[15]Schajer G S, Prime M B. Use of inverse solutions for residual stress measurement[J]. Journal of Engineering Materials and Technology, 2006, 128(3): 375−382.

[16]Virkar A V. Determination of residual stress profile using a strain gage technique[J]. Journal of the American Ceramic Society,1990, 73(7): 2100−2102.

[17]Cheng W, Finnie I, Vardar Ö. Deformation of an edge-cracked strip subjected to normal surface traction on the crack face[J].Eng Fracture Mech, 1992, 42: 97−108.

[18]Fuh K H, Wu C F. A residual-stress model for the milling of aluminum alloy (2014-T6)[J]. Journal of Materials Processing Technology, 1995, 51: 87−105.