土的结构性参数与强度的关系及其在边坡稳定分析中的应用

陈昌禄 ，邵生俊，邓国华

(1. 西安理工大学 岩土工程研究所，陕西 西安，710048；2. 河南理工大学 土木工程学院，河南 焦作，454000)

土的结构性是天然岩土材料在沉积过程中形成的空间排列和粒间联结作用所表现出的力学效应。Terzaghi[1]研究了这种结构性对土力学性质的影响，Skempton等[2−4]通过试验对此进行了验证。由于天然土材料的复杂性，以往人们主要以给定级配条件下人工制备的正常固结土、超固结土和松砂、密砂为研究对象，建立相应的强度、变形本构模型[5−10]，进而对工程问题进行分析。但是，在实际工程中，大多数土材料具有结构性，其力学特性与正常固结土和超固结土有显著差异。因此，通过这种手段分析实际工程问题所表现的性态存在较大的误差。目前，人们对结构性研究的细观形态学途径、固体力学途径和土力学途径进行了研究并取得了较大的进展[11]，其中扰动状态理论[12−13]、岩土破损力学[14]、综合结构势思想[5]以及四维空间理论[15]都是这方面的典型代表。谢定义等[5−7]通过对比上述分析方法的优、缺点后认为，应寻求1个参数来独立、有效地表征土结构性及其变化的力学效应，并提出了综合结构势思想，提出了1个反映土结构性的定量化参数。之后，邵生俊等[9−10,16−18]完善并发展了这一思想，提出了多个结构性参数，分析了结构性参数与土强度和变形之间的关系，建立了结构性本构模型。但是，到目前为止，基于综合结构势思想的结构性研究仍处于试验和理论分析阶段，并没有将其用来指导工程实际问题。通过研究结构性参数与土强度和变形之间的关系，进而建立结构性参数本构模型，实现数值分析并应用于工程实践，这是结构性参数常规的应用方法，也可以称为间接的应用方法。目前，虽然建立了不少本构模型，但将其真正应用于工程的实例很少。结构性是土的基本属性，因此，可以将结构性参数直接看作土的物性指标，以定量地指导工程实践，这称为结构性参数的直接应用方法。为此，本文作者从后者着手，分析天然黄土边坡开挖过程中结构性的变化规律，并讨论边坡的稳定性与结构性参数之间的关系。

1 黄土结构性参数分析

谢定义等[5−6]利用压缩试验分别测试了人工制备结构性土、重塑土和饱和土的压缩变形过程，并提出了1个反映结构性的定量化结构性参数即应变结构性参数，认为土的结构性可以从结构可稳性和结构可变性 2个方面来反映。邵生俊等[9−10]将其推广到三轴剪切试验条件下，通过原状黄土、重塑黄土和原状饱和黄土三轴剪切试验，提出了主应力 σ1，σ2，σ3和应力结构性参数 mσ之间的关系式。通过(σ1−σ3)y，(σ1−σ3)r和(σ1−σ3)s来反映扰动、浸水和加荷作用下土的结构性变化。其中：(σ1−σ3)y表示天然沉积黄土剪切过程结构性变化条件下的主应力差；(σ1−σ3)r和(σ1−σ3)s分别表示扰动重塑土和浸水饱和土的主应力差。

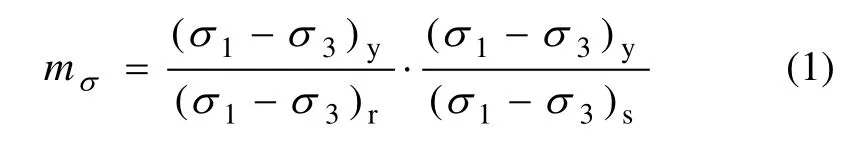
为了应用方便，邵生俊等[9]进一步给出了结构性参数mσ和广义剪应变εs之间的关系式：

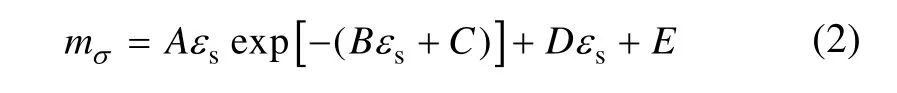
式中：A，B，C，D和E均为试验参数。取A=1.00；B=0.85。C，D和E分别由下述计算式确定：

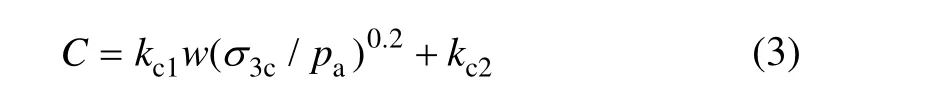
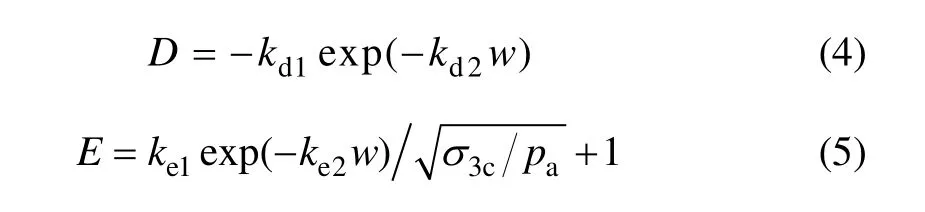
其中：pa和w分别为大气压和含水率；kc1=25.61，kc2=−5.52，kd1=1.734，kd2=15.390，ke1=33.340，ke2=11.430，它们均为试验参数。

式(3)和(5)建立了C，E与含水量和固结围压之间的关系，式(4)建立了D与含水量之间的关系。因此，该结构性参数实际上综合反映了含水率、固结压力和剪切变形3个方面的影响，其变化规律如图1和图2所示。由图1和图2可见：随着含水量、固结压力以及剪切变形的增大，土的结构性逐渐减弱，最终趋于稳定值 1。根据综合结构势理论，可以认为，结构性参数等于1的土为无结构性土，即正常固结土。

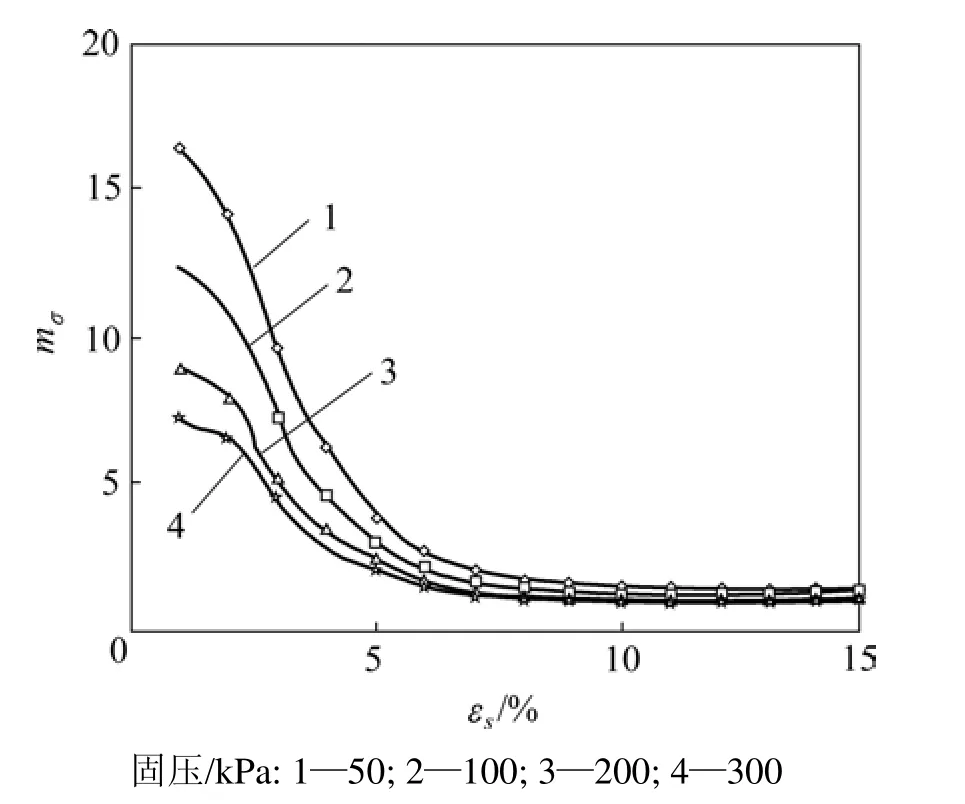
图1 含水量为8.5%时的结构性参数Fig.1 Structural parameter when water content of loess is 8.5%

图2 围压为100 kPa时的结构性参数Fig.2 Structural parameter under surrounding press of 100 kPa

2 结构性参数与强度的关系

土在变形过程中，土结构性参数变化的过程实际上是土颗粒相对位移导致土强度发挥的过程，因此，反映土结构的参数与反映土强度的参数之间必然存在密切的关系。摩尔−库仑屈服条件在土力学中有广泛的应用，但摩尔−库仑准则对于结构性土不完全适用[6]。若在摩尔−库仑准则中引入土的结构性参数，并以此来反映结构性土的强度特征，则可以起到简化分析问题的作用。

考虑结构性影响的摩尔−库仑准则可写为：

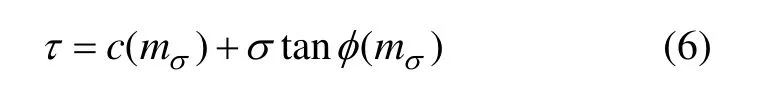
图3和图4所示为结构性参数与黏聚力和内摩擦角的关系。可见：黏聚力与结构性参数之间符合双曲线关系，而内摩擦角随结构性参数的变化而没有变化。这说明随着黄土结构性逐渐被破坏，颗粒间的胶结作用逐渐减弱，黏聚力减低；当土的结构性遭到彻底破坏时，黏聚力趋近于 0，此时，无结构性的土与饱和正常固结黏土和砂土的力学性质类似；随着黄土结构性的破坏，颗粒的摩擦特性基本没什么变化，摩擦角不变。对于某一剪切过程，黏聚分量在较小应变(1%)时达到最大值，而后迅速破坏；当结构性彻底破损时，唯一的强度分量是摩擦强度。

黏聚力与结构性参数的关系为：

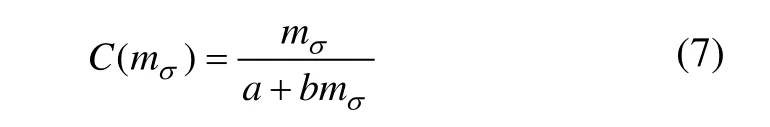
式中：a和b均为拟合参数，a=0.045 0，b=0.002 2。

图3 固结围压为0～300 kPa时黏聚力与结构性参数之间的关系Fig.3 Relationship between cohesion and structure parameter under surrounding press of 0−300 kPa

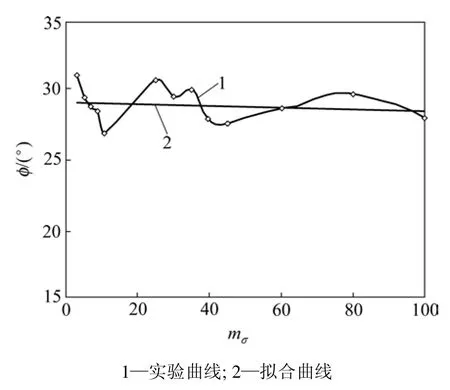
图4 固结围压为0～300 kPa时内摩擦角与结构性参数之间的关系Fig.4 Relationship between friction angle and structure parameter under surrounding press of 0−300 kPa

3 计算原理和思路

目前进行边坡稳定分析时，主要采用极限平衡和强度折减法。极限平衡法计算方法简单，物理意义明确，但在稳定分析之前，首先需要假定1个潜在的滑动破坏面，对同一个边坡假定不同的滑动面，求出不同的安全系数，这就使得计算结果具有不确定性。强度折减法的基本思路是:在计算过程中，将土的强度参数逐步降低，而使结构达到极限状态[19]。

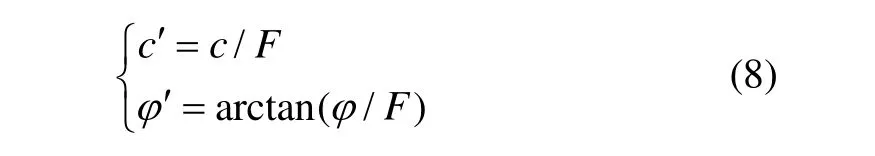
张鲁瑜等[20−23]认为，目前，强度折减法中土体破坏的标准尚未统一。在历史沉积多年后形成的天然黄土边坡具有一定的结构性。在实际工程中，对天然斜坡进行开挖后，由于围压的减小和应变的增大使得黄土的结构性逐渐被破坏，变形逐渐增大，最终导致滑移面形成，边坡失稳。由以上分析可知：结构性参数反映了围压、含水量、广义剪应变三者的综合影响，同时也是强度变化的内在因素。边坡的强度破坏主要是结构性变化引起的，强度折减也反映了结构性参数的变化。因此，引入反映土结构的结构性参数来评价边坡的稳定性更具有理论意义。

本文采用有限元极限平衡和人工折减强度相结合的方法计算开挖边坡的应力应变场。在此过程中计算结构性参数分布的变化，对结构性参数分布进行分析，进而评价边坡的稳定性。具体思路为：

(1) 开挖形成边坡后，计算该边坡的最小主应力场、广义剪应变场、结构性参数场以及安全系数，分析结构性参数分布的变化规律。

(2) 开挖形成边坡后，根据式(8)中的人工折减强度，在不同折减系数下计算边坡的最小主应力场、广义剪应变场、结构性参数分布以及安全系数，分析比较在不同折减系数下结构性参数分布的变化规律。

(3) 综合比较上述规律后，分析找出结构性参数和边坡稳定性之间的规律，进而给出由结构性参数变化来判断边坡稳定性的方法。

4 天然黄土边坡开挖的结构性参数变化规律

4.1 模型的建立和参数的选择

模型选用天然黄土边坡，边坡采用5步开挖。共开挖 20 m，边坡坡比为 1：0.7，以此形成开挖边坡。几何模型及网格划分见图5。土的本构模型选用摩尔−库仑模型，模型参数见表1。

4.2 计算结果

开挖形成边坡后，对边坡土的强度参数进行人工折减。将折减系数和利用极限平衡方法计算的安全系数进行比较，同时分析在不同折减系数下广义剪应变场和结构性参数分布规律。

表1 模型参数Table 1 Model parameters

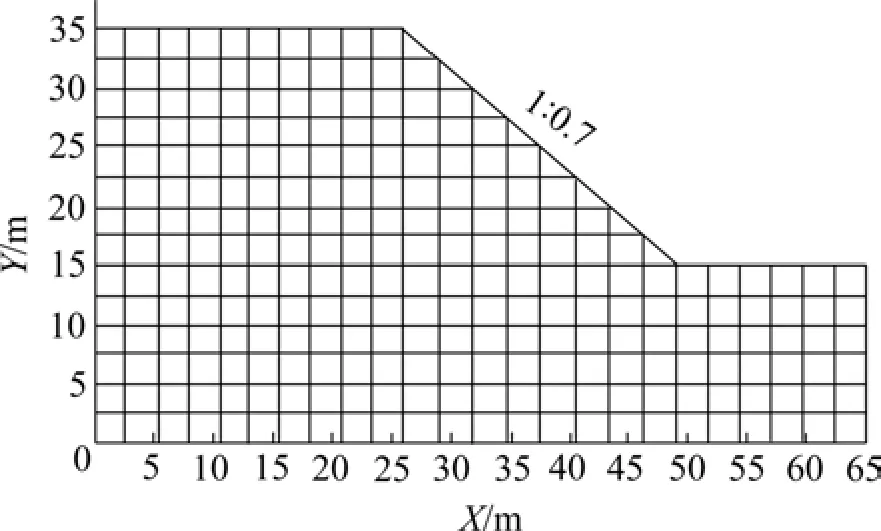
图5 几何模型及网格划分Fig.5 Geometric model and finite-element mesh

4.2.1 广义剪应变

图6所示为不同强度折减系数下开挖边坡的广义剪应变分布曲线。从图6可以看出：随着折减系数的增大，广义剪应变由坡角底部向坡顶上方扩展；当折减系数达到一定值时，整个边坡内某一幅值的广义剪应变从坡角到坡顶贯通，边坡达到临界破坏状态，此时，折减系数即为边坡的安全系数。在本例中，当折减系数为 2.15时(可以计算在此折减系数下边坡的安全系数为 1.006)，边坡处于临界破坏状态，由此确定边坡的安全系数为2.150。

图6 不同折减系数下边坡的广义剪应变场Fig.6 Changes of extended shear strain with different reduction factors

4.2.2 结构性参数

不考虑含水量变化的影响，结构性参数只取决于广义剪应变和围压的变化。边坡开挖后，将边坡土体的强度参数进行折减得到不同折减系数下的结构性参数，如图7所示。从图7可以看出：随着边坡的折减系数不断增大(安全系数不断减小)，结构性参数场具有与广义剪应变场相同的变化趋势。就本计算模型及参数而言，当折减系数为1.00(安全系数为2.120)时，结构性参数场几乎不形成带状，只有某一幅值的结构性参数有一个很小的带；但随着折减系数的增大，这一幅值的结构性参数场逐渐形成一个明显的带，并且有逐渐发展扩大的趋势；当强度参数折减到使边坡达到临界状态时(折减系数为2.150)，结构性参数场明显形成了一个贯穿区域，表明边坡达到极限平衡状态。此时的折减系数即为该边坡的安全系数。

5 结构性参数在判断边坡稳定性中的应用

边坡稳定性评价中需要解决的主要问题就是确定最小安全系数以及与最小安全系数相对应的临界滑动破坏面位置[23]。土的结构性是土颗粒空间排列和粒间联结作用的力学效应。土的结构联结没有遭到破坏以前表现为它维持结构可稳性的能力与颗粒联结的特性及稳定性有关。在结构联结遭到破坏以后表现为结构可变性的能力，与颗粒的排列特性与均匀性有关。在边坡开挖工程中，由于应力的释放和变形的增大使得土的结构性发生变化。结构性参数体现了应力和变形的共同作用，它反映了边坡开挖过程中的应力释放程度和变形协调关系，因此，用结构性参数的变化规律来判断边坡的稳定性更具有合理性。

(1) 当结构性参数的某一幅值形成一个贯穿区域时，即可认为该边坡达到极限平衡状态，此时的安全系数即为该边坡的最小安全系数，该结构性参数形成的贯穿区域可认为是边坡的滑动破坏面。

(2) 在边坡开挖卸荷过程中，结构性参数不断变化。考察不同折减系数下，在边坡水平方向(本例取坡脚Y=15 m，其他水平方向均有相似规律)结构性参数的变化情况，如图8所示。

图7 不同折减系数下边坡的结构性参数分布Fig.7 Changes of structural parameter in different reduction factors

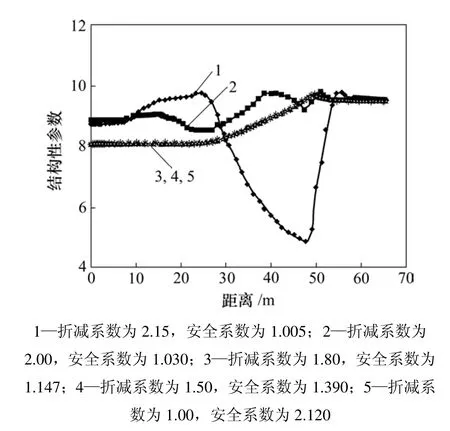
图8 Y=15 m时水平方向的结构性参数Fig.8 Changes of structural parameter in side slope horizontal direction when Y=15 m

从图8可以看出：当折减系数较小(即边坡安全系数较高)时，边坡在水平方向的结构性参数变化并不大；而当折减系数达到边坡极限平衡状态时，结构性参数在水平方向变化较大，先减小后增大，明显出现1个拐点。由此也可以利用结构性参数的变化来判断边坡是否达到极限平衡状态。

6 结论

(1) 基于已经建立的三轴应力条件下的结构性参数，分析了结构性参数与抗剪强度指标之间的规律，提出了结构性参数与强度参数之间的关系。

(2) 结构性与土强度密切相关。结构性是控制边坡稳定性的核心因素和内在原因，边坡的破坏主要是强度破坏，而强度破坏的内在因素主要是土的结构性参数降低，这使得人工强度折减更具有实际意义。

(3) 通过在边坡开挖过程中结构性参数的变化规律确定边坡的最小安全系数以及临界滑动面的位置。当边坡某一幅值的结构性参数形成贯穿区域时，该边坡处于临界滑动状态，此时，安全系数为该边坡的最小安全系数，结构性参数形成的贯穿区域为该边坡的临界滑动面。

[1]Terzaghi K. Theoretical soil mechanics[M]. New York: Weley,1943.

[2]Skempton A W. Note on the compressibility of clays[J]. Q J Geological Soc, 1994(100): 119−135.

[3]Skempton A W. The consolidation of clays by gravitational compaction[J]. Quarterly Journal of Geology Society, 1970, 125:373−411.

[4]Levoueil S, Vaughan P R. The general and congruent effects of structure in natural soil and weak rock[J]. Geotechnique, 1990,40(3): 467−488.

[5]谢定义, 齐吉琳. 土结构性及其定量化参数研究的新途径[J].岩土工程学报, 1999, 20(2): 651−656.XIE Ding-yi, QI Ji-lin. Soil structure characteristics and new approach in research on its quantitative parameter[J]. Chinese Journal of Geotechnical Engineering, 1999, 20(2): 651−656.

[6]谢定义, 齐吉林, 朱元琳. 土的结构性参数及其强度变形关系[J]. 水利学报, 1999, 30(10): 1−6.XIE Ding-yi, QI Ji-lin, ZHU Yuan-lin. Soil structure parameter and its relations to deformation and strength[J]. Journal of Hydraulic Engineering, 1999, 30(10): 1−6.

[7]谢定义, 齐吉林, 张振中. 考虑结构性的本构关系[J]. 土木工程学报, 2000, 33(4): 35−41.XIE Ding-yi, QI Ji-lin, ZHANG Zhen-zhong. A constitutive laws considering soil structural properties[J]. China Civil Engineering Journal, 2000, 33(4): 35−41.

[8]JIANG Ming-jing, SHEN Zhu-jiang. Microscopic analysis of shear band in structured clay[J]. Journal of Hydraulic Engineering, 1998, 20(2): 102−108.

[9]邵生俊, 周飞飞, 龙吉勇. 原状黄土结构性及其定量化参数研究[J]. 岩土工程学报, 2004, 26(4): 531−536.SHAO Sheng-jun, ZHOU Fei-fei, LONG Ji-yong. Structural properties of loess and its quantitative parameter[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(4): 531−536.

[10]邵生俊, 龙吉勇, 于清高, 等. 湿陷性黄土的结构性参数本构模型[J]. 水利学报, 2006, 37(11): 1315−1322.SHAO Sheng-jun, LONG Ji-yong, YU Qing-gao, et al. A constitutive model of collapsible loess with structure parameter[J]. Journal of Hydraulic Engineering, 2006, 37(11):1315−1322.

[11]沈珠江. 土体结构性的数学模型—21世纪土力学的核心问题[J]. 岩土工程学报, 1996, 18(1): 95−97.SHEN Zhu-jiang. Mathematical model of soil structure characteristics[J]. Chinese Journal of Geotechnical Engineering,1996, 18(1): 95−97.

[12]王国欣, 肖树芳, 黄宏伟, 等. 基于扰动状态概念的结构性黏土本构模型研究[J]. 固体力学学报, 2004, 25(2): 191−197.WANG Guo-xin, XIAO Shu-fang, HUANG Hong-wei, et al.Steal study of constitutive model of structural clay based on the disturbed state concept[J]. Acta Mechanica Solida Sinica, 2004,25(2): 191−197.

[13]周成, 沈珠江, 陈生水, 等. 结构性土的次塑性扰动状态模型[J]. 岩土工程学报, 2004, 26(4): 435−439.ZHOU Cheng, SHEN Zhu-Jiang, CHEN Sheng-shui, et al. A hypoplasticity disturbed state model for structured soils[J].Chinese Journal of Geotechnical Engineering, 2004, 26(4):435−439.

[14]陈铁林, 沈珠江. 岩土破损力学的系统论基础[J]. 岩土力学,2004, 25(11): 21−26.CHEN Tie-lin, SHEN Zhu-jiang. System approach of breakage mechanics for geological materials[J]. Rock and Soil Mechanics,2004, 25(11): 21−26.

[15]Liu M D, Carier J P. Virgin compression of structured soils[J].Geotechnique, 1999, 49: 143−157.

[16]邵生俊, 龙吉勇, 周飞飞. 湿陷性黄土结构性变形特性分析[J]. 岩土力学, 2006, 27(10): 1668−1672.SHAO Sheng-jun, LONG Ji-yong, ZHOU Fei-fei, et al. Analysis of structural deformation properties of collapsible loess[J]. Rock and Soil Mechanics, 2006, 27(10): 1668−1672.

[17]骆亚生. 非饱和黄土在动、静复杂应力条件下的结构变化特性及结构性本构关系研究[D]. 西安: 西安理工大学岩土所,2005.LUO Ya-sheng. Variation characteristics of soil structure and structural constitutive relation of unsaturated loess under static and dynamic complex stress conditions[D]. Xi’an: Institute of Geotechnical Engineering, Xi’an University of Technology,2005.

[18]陈存礼, 高鹏, 何军芳. 考虑结构性影响的原状黄土本构关系[J]. 岩土工程学报, 2007, 29(9): 1330−1336.CHEN Cun-li, GAO Peng, HEN Jun-fang. Constitutive relationship of intact loess considering structural effect[J].Chinese Journal of Geotechnical Engineering, 2007, 29(9):1330−1336.

[19]Zienkiewicz O C, Humpheson C L R W. Associated and non-associated visco-plasticity and plasticity in soilmechanics[J].Geotechnique, 1975, 25(4): 671−689.

[20]张鲁渝, 郑颖人, 赵尚毅, 等. 有限元强度折减系数法计算土坡稳定安全系数的精度研究[J]. 水利学报, 2003, 34(1): 21−23.ZHANG Lu-yu, ZHENG Ying-ren, ZHAO Shang-yi, et al. The feasibility study of strength2reduction method with FEM for calculating safety factors of soil slope stability[J]. Journal of Hydraulic Engineering, 2003, 34(1): 21−23.

[21]郑颖人, 赵尚毅. 有限元强度折减法在土坡与岩坡中的应用[J]. 岩石力学与工程学报, 2004, 23(19): 3381−3388.ZHENG Ying-ren, ZHAO Shang-yi. Application of strength reduction fem in soil and rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3381−3388.

[22]刘金龙, 栾茂田, 赵少飞, 等. 关于强度折减有限元方法中边坡失稳判据的讨论[J]. 岩土力学, 2005, 26(8): 1345−1348.LIU Jin-long, LUAN Mao-tian, ZHAO Shao-fei, et al.Discussion on criteria for evaluating stability of slope in elastoplastic FEM based on shear strength reduction technique[J].Rock and Soil Mechanics, 2005, 26(8): 1345−1348.

[23]刘金龙, 陈陆望, 王吉利. 边坡稳定性分析方法简述[J]. 水电能源科学, 2008, 26(1): 133−136.LIU Jin-long, CHEN Lu-wang, WANG Ji-li. Refining on methods of slope stability analysis[J]. Water Resources and Power, 2008, 26(1): 133−136.