索拱组合结构的动力建模及其内共振分析

吕建根 ，赵跃宇，王荣辉

(1. 华南理工大学 土木与交通学院，广东 广州，510641；2. 仲恺农业工程学院 城市建设学院，广东 广州，510225；3. 湖南大学 土木工程学院，湖南 长沙，410082)

1 索拱组合结构的动力学方程

索拱组合结构模型如图1所示。为了建模方便，将索的运动在坐标系xOy中描述，拱的运动在中描述。图1中：θc和θg分别为索和拱的水平倾角；lc和lg分别为索和拱在相应坐标系中的跨度；dc和dg分别为索的初始垂度和拱的矢高。

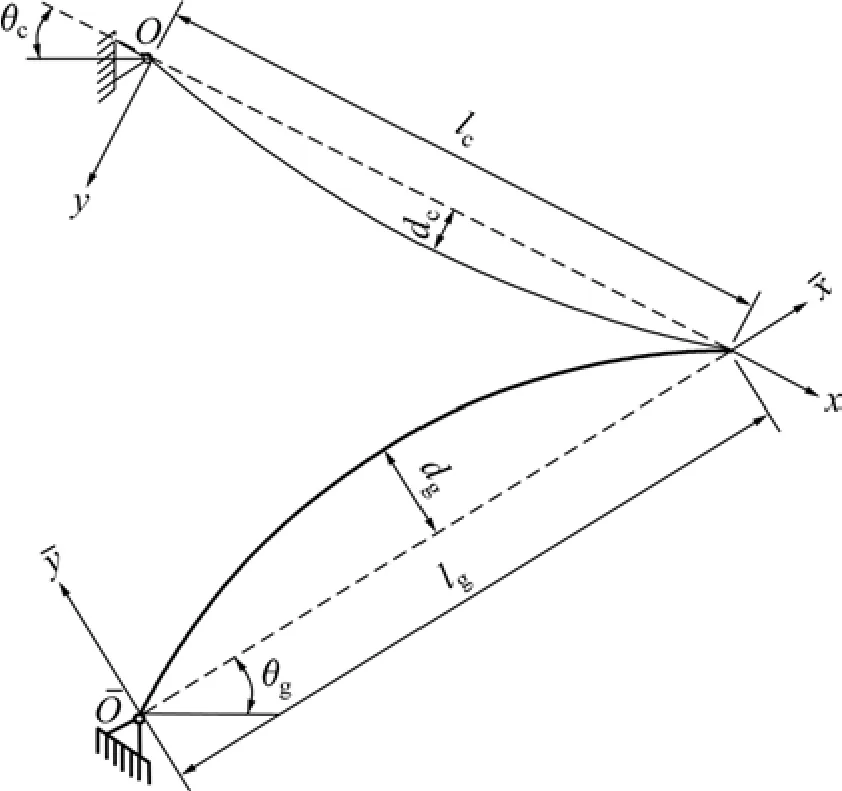
图1 索拱组合结构相互作用分析模型Fig.1 Mechanical model of cable-stayed arch

对于如图1所示坐标系，索和拱在右端端点铰接。根据位移协调条件，其连接关系式如下：

式中：ug和uc分别为拱和索在长度方向的纵向位移；vg和vc分别为拱和索的横向振动位移。

根据索的三维非线性运动控制方程[12]，通过化简整理可得到拉索平面运动学方程：

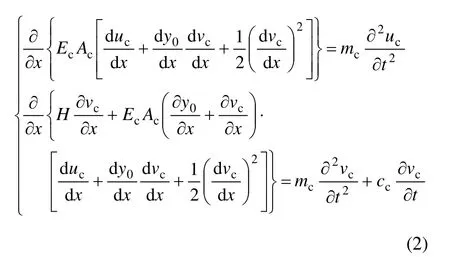
式中：EcAc为索的抗压刚度；mc为索的单位长度质量；H为索的初始张力；y0为斜拉索的初始线性方程，为x的函数；cc为弹性索的结构阻尼系数。

由于弹性索纵向变形远小于其横向变形，而横向振动频率与纵向振动频率相差很大，因此，纵向惯性力可以忽略。将式(2)中第 1式两边同时对 xc在区间[0, lc]内积分，结合式(1)，可以得到弹性索在考虑纵向位移后的横向运动微分方程：

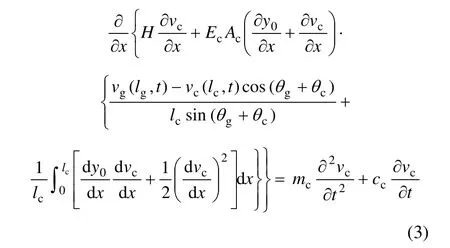
在大跨度缆索吊装施工过程中，悬臂拱在如图1所示的局部坐标系下，悬臂拱的矢跨比 dg/lg通常都小于 1/10，可以将吊装过程中的悬臂拱当成浅拱考虑[13]，得到考虑右端点纵向位移后拱横向运动微分方程[14−15]：

我国会计法律法规对会计人员的职业行为和专业素质提出了更高要求，国家关于会计工作的相关法律法规，职业道德要求是每一名会计人员在日常工作中必须遵守的规范。通过对会计人员继续教育培训，确保会计队伍全面掌握最新的法律法规，以及对会计人员工作行为的要求。在全新的历史时期，我们应该充分认识到会计人员继续教育也是国家法律法规管理工作提出的新要求，是加强会计队伍有效管理的重要组成部分，更是加强会计人才队伍建设的重要内容。开展会计人员继续教育培训的目的是为了提高会计人员的政治素养、业务能力、职业道德水平，使其及时更新专业知识，补充和拓展专业素质。

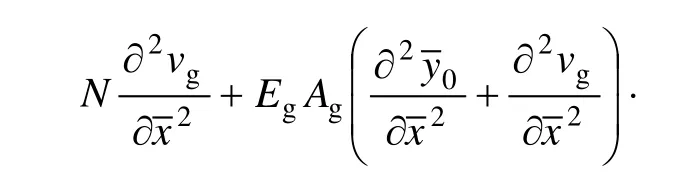
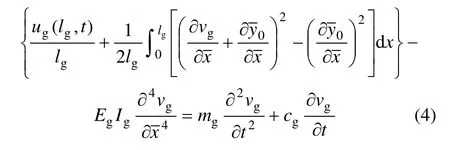
将式(1)中的第1式代入式(4)，得到：

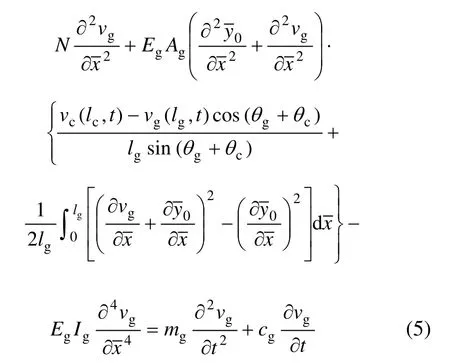
式中：N为拱的初始轴向力；EgIg为拱的面内抗弯刚度；为拱在局部坐标系中的初始拱轴线方程；cg为弹性拱的结构阻尼系数；mg为拱的单位长度质量；EgAg为拱的抗压刚度。

联立式(3)和式(5)，即得到索拱组合结构耦合横向运动方程。

2 索拱组合结构的内共振分析

在拱桥施工过程中的索拱组合结构中，扣索的自振频率通常比弹性拱的自振频率低很多，索拱之间相互激励而产生的内共振往往是扣索的高阶与弹性拱的低阶振动，因而，在对索拱组合结构相互作用的内共振分析过程中，必须包括索拱的高阶模态。下面对索拱耦合运动方程(3)和式(5)进行 Galerkin高阶模态截断，设

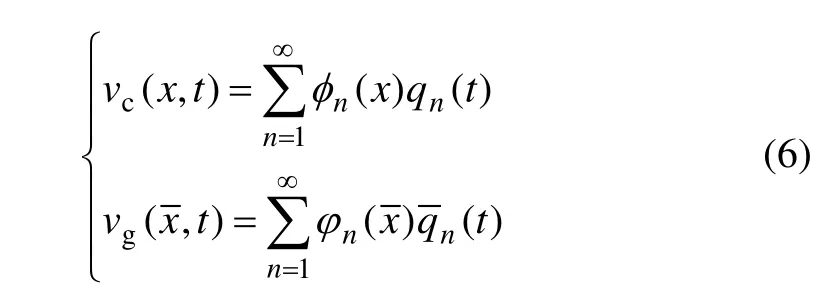
其中： φn(x)和ϕn(x)分别为索和拱的振型函数；qn(t)和( t )分别为索和拱的振动函数。

将式(6)代入式(3)和式(5)，在式(3)两边乘以 φi(x)并在[0, lc]内积分，在式(5)式两边乘以ϕi()并在[0, lg]内积分，利用振型函数的正交性，得到索拱组合结构

多阶离散动力学方程：

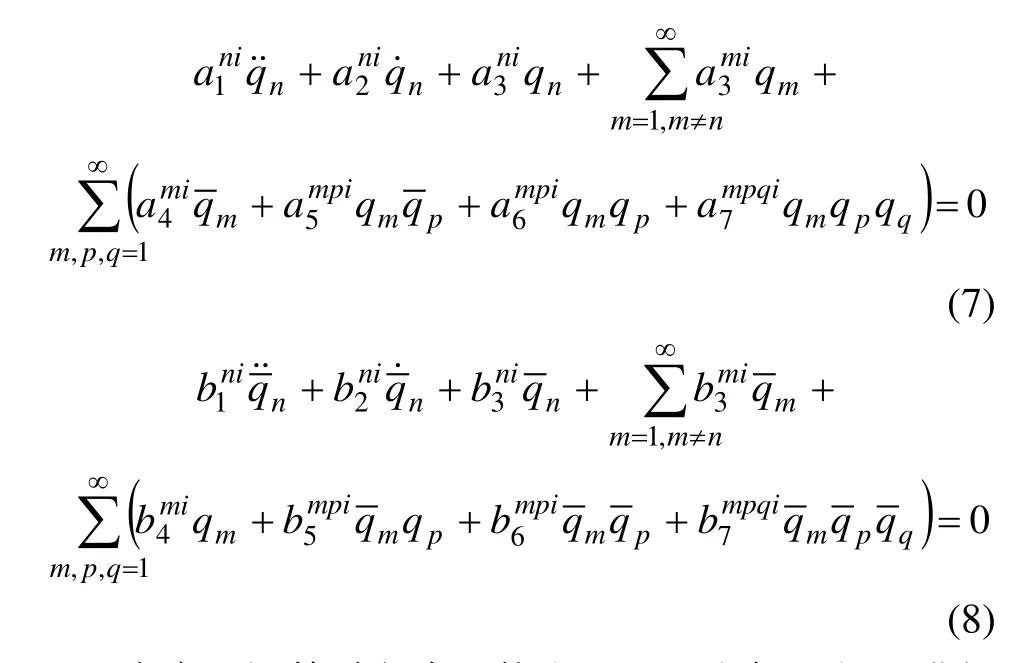
在实际运算过程中，均取 i=n。对式(7)和(8)进行化简，对式(7)两边同除以，对式(8)两边同除以，引入任意小的正数ε，并定义系数(见文献[16])，代入式(7)和式(8)，可得到：

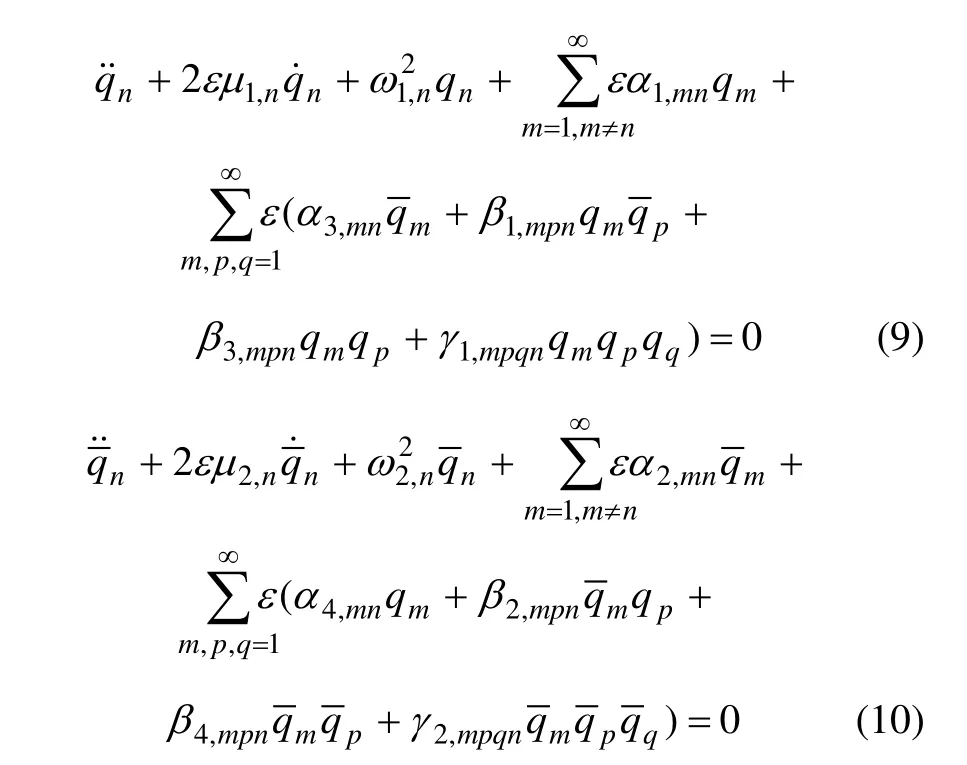
采用多尺度摄动方法寻找qn和的一致渐近解，引入快变时间尺度T0=t和慢变时间尺度T1=ε t ，设解的形式如下：

将式(10)代入式(9)，可以得到索拱组合结构的一阶近似方程：

式(11)复数形式的解为：

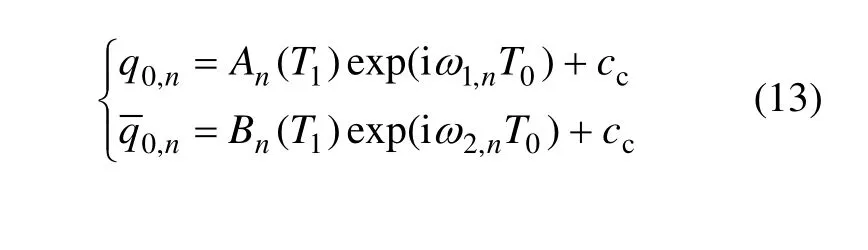
将式(12)代入二阶近似方程并整理得：

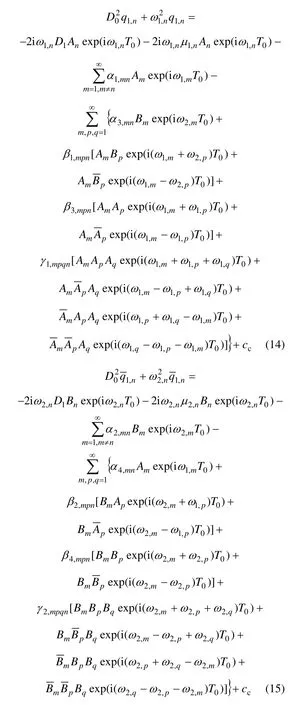
式中：cc为 c相应的共轭项。从式(13)可以看出：当时，索和拱之间存在相互作用的内共振；同时，由于索和拱的自振频率相差很大，若进行低阶模态截断，则只有索和拱自身模态之间的亚谐波和超谐波内共振产生，索拱之间不会相互作用而产生内共振，但是，若考虑索和拱的高阶模态，则在索的高阶模态和拱的低阶模态之间将产生内共振。因此，对索和拱组合结构体系进行相互作用的非线性动力学分析时，应进行高阶模态截断，而且随着模态的增加，内共振模式将大大增加。

3 索拱组合结构内共振的数值模拟

为了证实所建立的索拱组合结构非线性动力学模型及分析理论的正确性，以某钢管混凝土拱桥缆索吊装施工过程中第1节段结构体系为数值研究对象，忽略扣塔振动的影响，建立索拱组合结构的非线性动力学力学模型(参考图1)，索和拱的结构参数分别见表1和表 2。求解方程系数，可知该结构体系为弱非线性动力学问题。

表1 索的结构参数Table 1 Structural parameters of cable

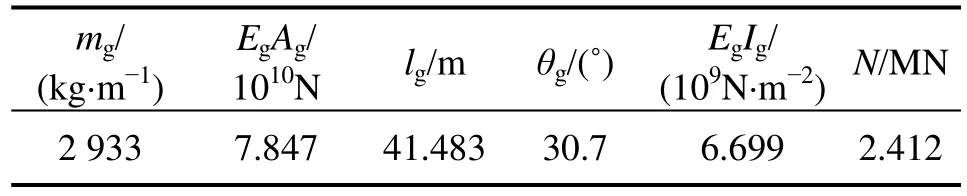
表2 拱的结构参数Table 2 Structural parameters of the arch

给定索和拱的初始位移均为0.01 m，绘制索和拱的100 s时间历程曲线，见图2。从图2可以看出：在非共振情形下，索和拱之间的振动相互耦合非常弱，索和拱的振幅都约等于初始位移，因此，若索拱组合结构的结构设计参数都处在结构的非共振区域以内，则索和拱的动力学特性可以单独进行分析，可不考虑振动时索和拱之间的相互影响。

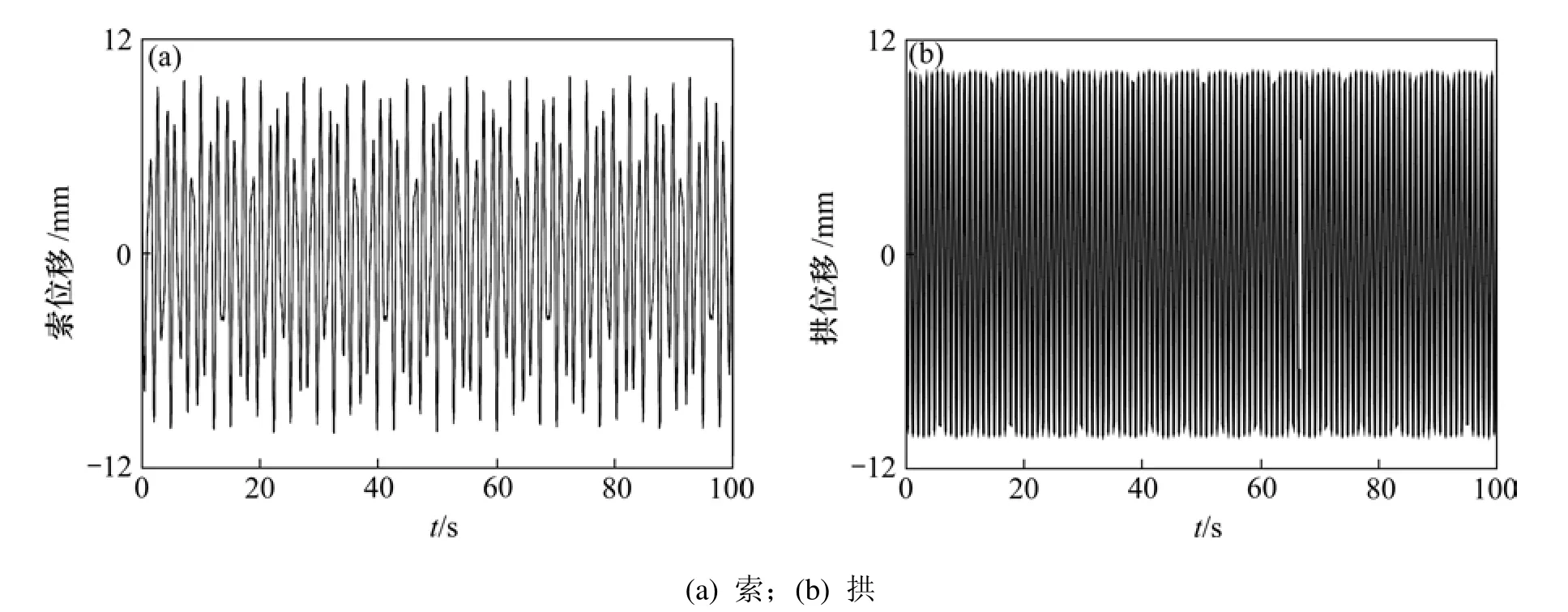
图2 索拱组合结构非内共振情形下的时间历程Fig.2 Time history of cable-stayed arch structure under non-resonance state

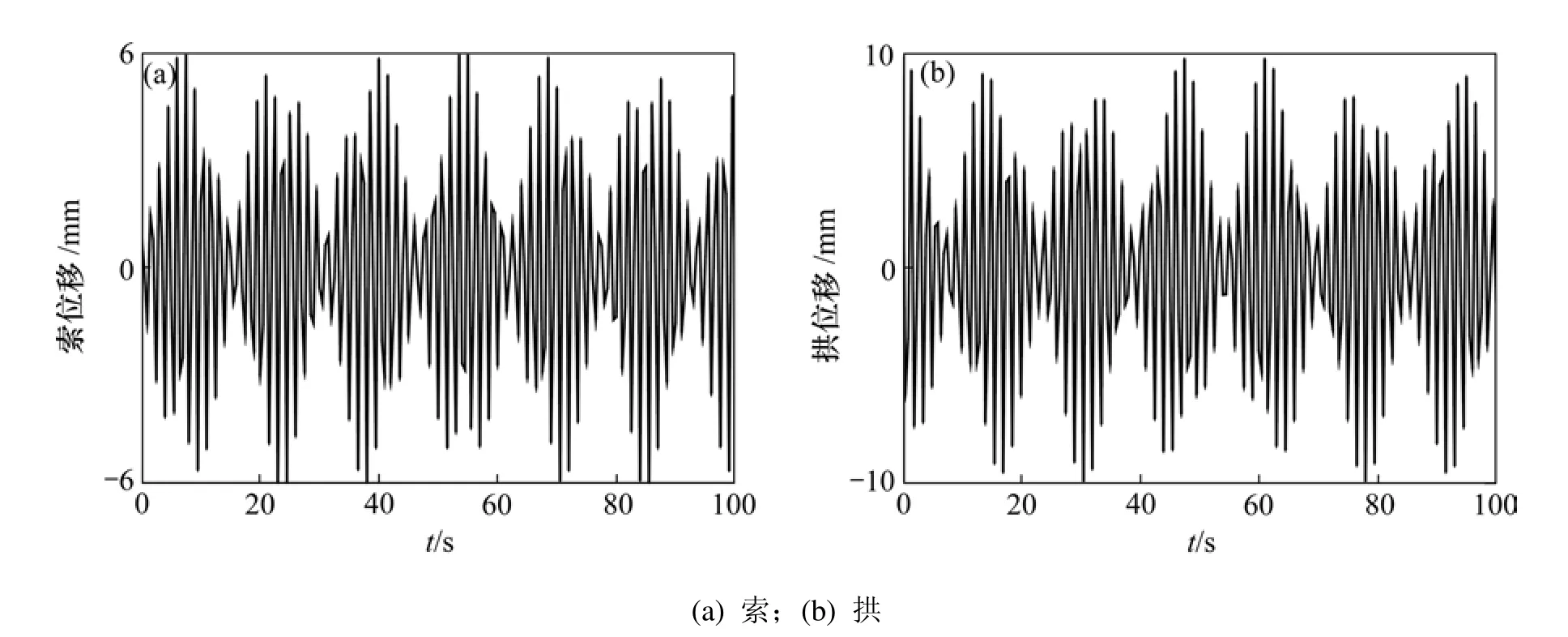
图3 索拱组合结构内共振情形下的时间历程Fig.3 Time history of cable-stayed arch under internal resonance state

从数值分析结果可知：在非内共振情况下，索和拱的最大振幅都与初始位移基本相同，分别为9.7 mm和 9.8 mm；而在内共振情况下，索的最大振幅达到60.5 mm，拱的最大振幅为9.9 mm。说明在内共振情况下，拱对索的激励效果非常明显，导致拉索产生大幅度振动，而索对拱的激励很小，基本上可以忽略。其主要原因是索拱相互激励的效果与索拱之间的单位质量比、抗压刚度比及抗弯刚度比等有密切关系。

4 结论

(1) 利用索拱组合结构的连接条件及边界条件，建立了索拱组合结构的非线性动力耦合运动学控制方程。

(3) 当索拱组合结构的结构设计参数都在非共振区域时，索和拱的动力学性质均可单独进行分析，并可不考虑耦合作用。

(4) 当结构设计参数在索和拱的内共振区域时，在设计过程中，索与拱之间的相互耦合作用是不容忽视的关键问题。

(5) 在索拱内共振时，一般可以忽略索对拱的激励，但不能忽略拱对索的激励，其激励效果与索拱之间的单位质量比、抗压刚度比及抗弯刚度比等有关。

[1]赵雷, 杜正国. 大跨度钢筋混凝土拱桥钢管混凝土劲性骨架施工阶段稳定性分析[J]. 西南交通大学学报, 1994, 29(4):446−452.ZHAO Lei, DU Zheng-guo. Analysis of stability during construction of the steel-tube concrete stiff skeleton of long-span RC arch bridge[J]. Journal of Southwest Jiaotong University,1994, 29(4): 446−452.

[2]陈宝春, 孙潮. 石潭溪大桥施工受力分析[J]. 中国公路学报,1998, 11(4): 51−57.CHEN Bao-chun, SUN Chao. Mechanic analysis of the construction phase of Shitanxi bridge[J]. China Journal of Highway and Transport, 1998, 11(4): 51−57.

[3]盛洪飞, 郭伟, 王锐, 等. 无风撑钢管混凝土中承拱桥非线性试验分析[J]. 哈尔滨建筑大学学报, 1997, 30(4): 103−108.SHENG Hong-fei, GUO Wei, WANG Rui, et al. The nonlinear analysis of concrete filled steel tubular half trough arch bridge without wind brace[J]. Journal of Harbin University of Architecture, 1997, 30(4): 103−108.

[4]陈宝春, 徐爱民, 孙潮. 钢管混凝土拱桥温度内力计算时温差取值分析[J]. 中国公路学报, 2000, 13(2): 52−56.CHEN Bao-chun, XU Ai-min, SUN Chao. Analysis of thermal difference magnitude in thermal inner force calculation of CFST arch bridge[J]. China Journal of Highway and Transport, 2000,13(2): 52−56.

[5]赵长军, 王锋君, 陈强, 等. 大跨度钢管混凝土拱桥空间稳定性分析[J]. 公路, 2001(2): 15−17.ZHAO Chang-jun, WANG Feng-jun, CHEN Qiang, et al.Analysis of space stability of steel pipe concrete arch bridge with large span[J]. Highway, 2001(2): 15−17.

[6]剧锦三, 郭彦林. 索−拱结构的平面内稳定性研究[J]. 建筑结构学报, 2001, 22(2): 84−87.JU Jin-san, GUO Yan-lin. Instability behavior in the plane of cable-arch structure[J]. Journal of Building Structures, 2001,22(2): 84−87.

[7]赵跃宇, 康厚军, 王连华, 等. 索−拱结构面内稳定性研究[J].湖南大学学报: 自然科学版, 2006, 33(3): 1−5.ZHAO Yue-yu, KANG Hou-jun, WANG Lian-hua, et al.Instability behavior in the plane of cable-arch structure[J].Journal of Hunan University: Natural Science, 2006, 33(3): 1−5.

[8]方淑君, 李德建, 曾庆元. 三线铁路预应力连续梁桥列车−桥梁时变系统空间振动分析[J]. 中南大学学报: 自然科学版,2008, 39(2): 394−399.FANG Shu-jun, LI De-jian, ZENG Qing-yuan. Stochastic space vibration analysis of prestressed continuous bridge time-varying system in three-track railroad[J]. Journal of Central South University: Science and Technology, 2008, 39(2): 394−399.

[9]Matsumoto M, Shiraishi N, Shirato H. Rain-wind induced vibration of cables of cable-stayed bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 41/44:2011−2022.

[10]汪至刚, 孙炳楠. 斜拉索的参数振动[J]. 土木工程学报, 2002,35(5): 28−33.WANG Zhi-gang, SUN Bing-nan. Parametric vibration of the cable in cable-stayed bridge[J]. China Civil Engineering Journal,2002, 35(5): 28−33.

[11]赵跃宇, 吕建根. 索−拱组合结构中斜拉索的非线性参数振动[J]. 土木工程学报, 2006, 39(12): 67−72.ZHAO Yue-yu, LÜ Jian-gen. Non-linear parametric vibration of cables in cable-arch composite structures[J]. China Civil Engineering Journal, 2006, 39(12): 67−72.

[12]王连华, 赵跃宇. 受支承运动作用的拉索大幅振动[J]. 土木工程学报, 2008, 41(8): 65−71.WANG Lian-hua, ZHAO Yue-yu. On the large amplitude vibrations of stay cables induced by support motions[J]. China Civil Engineering Journal, 2008, 41(8): 65−71.

[13]XU Jian-xue, HUANG Hong, ZHANG Pei-zhen. Dynamic stability of shallow arch with elastic Supports-application in the dynamic stability analysis of inner winding of transformer during short circuit[J]. International Journal of Non-linear Mechanics,2002, (37): 909−920.

[14]Lakrad F, Schiehlen W. Effects of a low frequency parametric excitation[J]. Chaos, Solitons and Fractals, 2004(22):1149−1164.

[15]Pinto O C, Goncalves P B. Active non-linear control of buckling and vibrations of a flexible buckled beam[J]. Chaos, Solitons and Fractals, 2002(14): 227−239.

[16]吕建根. 大跨度索拱组合体系非线性静动力性能研究[D]. 长沙: 湖南大学土木工程学院, 2007.LÜ Jian-gen. The research on nonlinear static-dynamic mechanics performance of long-span cable-stayed arch system[D]. Changsha: School of Civil Engineering, Hunan University, 2007.