五坐标加工中非线性误差校核及超差处理方法的研究*

李永桥 陈 强 谌永祥

(西南科技大学制造科学与工程学院，四川绵阳 621010)

各种CAD/CAM系统前置处理阶段，一般都采用弧弦逼近方式，以工件不动，刀具运动的原则，按精度要求将自由曲面离散成一系列微小直线段，得到走刀步长和加工宽度，最终获得刀位数据。由于曲面曲率不断变化，曲面各点的法向矢量的变化导致刀轴矢量不断变化，所以当采用五坐标数控机床加工工件时，刀具的运动形式是各移动轴和旋转轴驱动下的合成运动，此时刀具相对于工件的运动轨迹已不再是离散而成的微小直线段，而是一条非线性的空间曲线，这条曲线与连接两切触点的直线之间的偏差是一种非线性误差，如何有效控制该误差是曲面加工技术中的一个重要问题。因此，对于五坐标加工，一般还需在后置处理中再根据刀位文件中的离散刀位信息对非线性误差进行有效计算并在超差时进行相应处理。

1 非线性误差的产生机理

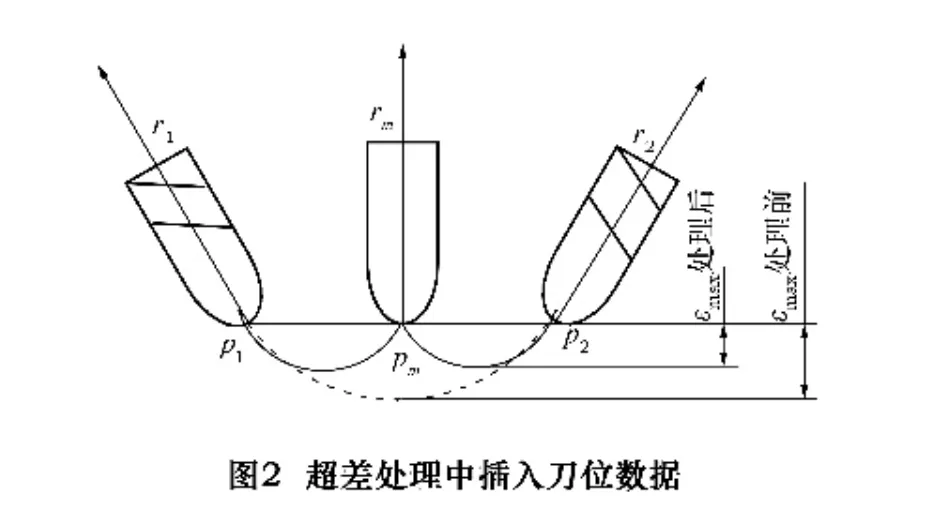
图1所示为五坐标加工过程中，相邻刀位点之间刀具的运动示意图，借此描述非线性运动误差的产生机理。其中：刀位轨迹数据由刀位点位置p和刀具轴线方向矢量r组成；pL(t)所描述的直线为理想中的编程曲线；当五坐标机床将非线性运动转换为各轴的线性插补运动时，其合成运动轨迹为p(t)所描述的实际加工曲线。p(t)偏离直线pL(t)，两者间的最大偏离量εmax即可近似作为非线性误差的估计。如前所述，该误差应该是三维意义下的误差，即p(t)实际是一条三维空间曲线，这里简单以二维图进行示意。

2 非线性误差的计算分析

本文采用基于机床运动模型正反算方法估算非线性误差，方法核心思想是：如图1所示，设相邻刀位数据为(p1，r1)、(p2，r2)，直线 p1p2经过点 p1、p2。首先通过正向机床运动模型变换，将相邻两个刀位数据由工件坐标系变换到机床坐标系，得到机床各个运动轴运动量。然后模拟数控系统线性插补算法，获得任意时刻机床各轴运动状态。最后，再将各时刻机床运动量由机床坐标系变换到工件坐标系下，得到各时刻刀具刀位点在工件坐标系中的坐标信息，并求得该点与直线p1p2的距离h。设所有时刻中，t时刻处获得最大的距离值ht，则ht便为该相邻刀位数据间的非线性误差。该方法可有效地对非线性误差进行近似估算，如此反复运用该方法，可获得整个刀位文件误差分布情况。其具体操作步骤如下：

(1)机床运动变换模型正算

以双转台A-B结构五坐标机床为例，设有相邻刀位数据为(p1，r1)、(p2，r2)，直线 p1p2经过点 p1、p2。经机床运动模型变换，得出机床各运动轴运动量分别为(X1，Y1，Z1，A1，B1)、(X2，Y2，Z2，A2，B2)。由于数控系统做线性插补，则从(X1，Y1，Z1，A1，B1)运动到(X2，Y2，Z2，A2，B2)的过程中，任意一时刻机床运动状态可描述为

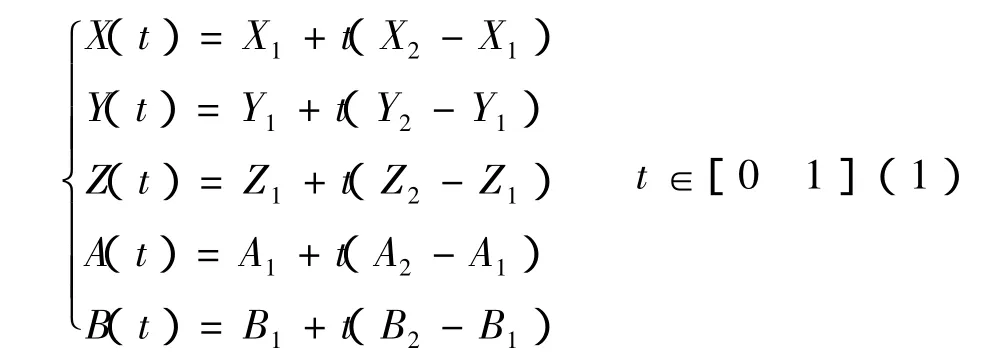
(2)机床运动变换模型反算

根据机床运动学变换模型理论可知，如果机床各个运动副的运动量为已知条件，则可计算刀具在工件坐标系下的刀轴矢量情况和刀位点情况，即：

(3)估算非线性误差

经过前两个步骤，得到了在时间段t内，各个时刻处工件坐标系下的刀位点 p(t)。设p(t)到直线p1p2的距离为 ε(t)，则：

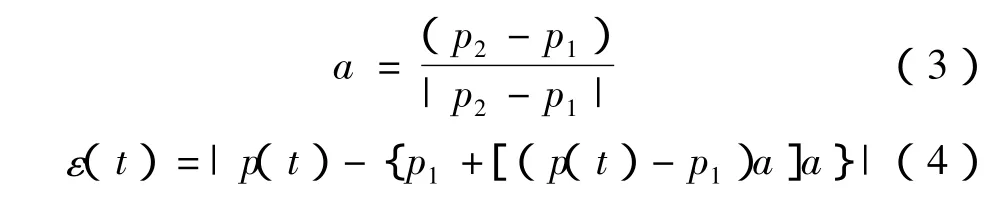
将ε(t)对参数t求导，设在t=ts取得最大值，则最大值 εmax为：

对于εmax的求解，由式(5)严格确定极为困难，实际求解中可根据非线性加工误差的分布情况，直接取中点，即 ts=0.5。

3 非线性误差的超差处理

当εmax大于允许值时则需要对该程序段进行处理，目前针对超差的处理方法归纳起来总共有3种：切触点偏置法、线性化法和自适应线性化法。切触点偏置法不能保证偏置刀触点后的误差在给定的误差范围内。线性化法会造成加工数据量急剧膨胀，影响机床加工能力，且当走刀步长过小时，还会造成机床振颤的现象。自适应线性化法首先是判断程序段非线性误差是否超差，然后将超差程序段刀位数据线性分割，减小步长和旋转角度对非线性误差的影响。

按照2节所述步骤计算相邻刀位数据非线性误差εmax，如果εmax小于误差许用值，则跳过该段数据，转入求解下段相邻刀位数据非线性误差。如果εmax大于误差许用值，如图2，则利用插入刀位数据方法对原刀位数据进行分割，插入的刀位点(pm，rm)计算公式为：

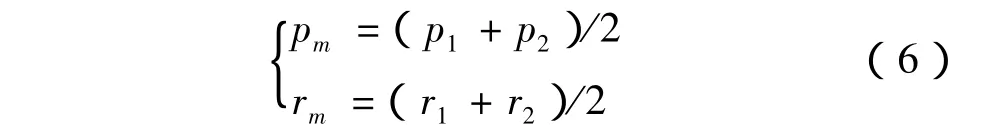
然后，计算对应于(pm，rm)的机床各轴位置(Xm，Ym，Zm，Am，Bm)，再次检验(p1，r1)和(pm，rm)间及(pm，rm)和(p2，r2)间的非线性误差，若仍然超差，则按上述过程继续插入新的刀位点，直至满足要求。超差处理流程如图3所示，本文根据如上所述的思路编制后置处理程序对原始刀位数据进行处理。

4 应用及仿真验证

以叶轮叶片加工为例，对非线性误差超差处理流程进行检验。如图4a所示，为CAD/CAM系统前置处理产生的刀具路径，获得的刀位文件中共有68条走刀语句，对其进行后置处理后，得到 NC代码文件，在VERICUT软件中模拟加工过程，如图4b所示，在叶片中部附近位置有明显的过切现象。

利用本文的非线性误差估算方法对该叶片的加工误差进行估算，获得非线性误差分布情况，如图5a所示。从图中可以看出，中部附近的相邻刀位语句间的非线性误差较大，该图也印证了图4b的加工结果。图5b反映了刀位文件描述的刀轴矢量在工件坐标系下的分布情况。

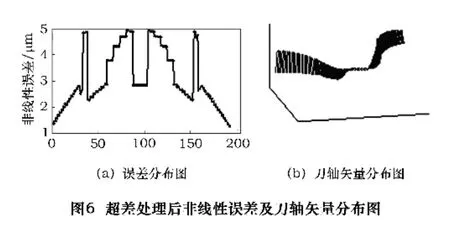
按照本文所述的非线性误差超差处理流程对该刀位文件进行处理，误差需用值取为ε=0.005 mm，得到新的共193条走刀语句的刀位文件。新的刀位文件其非线性误差分布情况如图6a所示。从图中可看出所有的非线性误差都被严格控制在误差许用值范围之内，获得了预期的结果。图6b显示了插入新的刀位数据后，新的刀位文件描述的工件坐标系下的刀轴矢量分布图。图7显示了利用新的刀位数据进行模拟加工的结果。结果显示，采用本文所述非线性误差超差处理方法产生的刀位文件，能正确驱动机床完成加工任务，同时消除工件中部附近的过切现象。

5 结语

非线性误差是五坐标数控加工中特有的，也是较难解决的问题。本文提出的非线性误差计算方法为五坐标机床的非线性误差判断提供了依据。此外提出的超差处理方法可根据加工对象的精度要求，对 CAM软件产生的刀位数据进行处理，使其非线性误差符合精度要求。通过编制程序，仿真验证了本文所述方法的正确性，从而为后置处理中超差处理提供了可靠依据。

［1］周艳红，周济，周云飞.五坐标数控加工的理论误差分析与控制［J］.机械工程学报，1999，35(5)：54-57.

［2］吴大中，王宇晗，冯景春，等.五坐标数控加工的非线性运动误差分析与控制［J］.上海交通大学学报，2007，41(10)：1608-1612.

［3］王丹，陈志同，陈五一.五轴加工中非线性误差的检测和处理方法［J］.北京航空航天大学学报，2008，34(9)：1003-1006.

［4］张健，赵福令，杨连文，等.五轴数控加工后处理关键技术分析与实现［J］.机床与液压，2007，35(1)：65-68.

［5］段春辉.五轴联动数控机床通用后置处理系统研制［D］.成都：西南交通大学，2007.

［6］周艳红，周济.数控加工技术［M］.北京：国防工业出版社，2002.

［7］丘立庆.数控加工编程通用后置处理器的研究与开发［D］.南宁：广西大学，2006.