Fitzhugh-Nagumo方程行波解及孤立波解

陈自高, 张金辉

(华北水利水电学院 数学与信息科学学院，河南 郑州 450011)

非线性发展方程被广泛用来描述科学领域内各种复杂的非线性现象，因而如何求解这些非线性发展方程具有重要的意义．近年来，多种获取非线性发展方程精确解的方法陆续被提出，如齐次平衡法[1]，双曲正切函数法[2]，试探函数法[3]， sine-cosine法[4]，扩充的双曲正切函数法[5]，修正的双曲正切函数法[6]， Jacobi椭圆函数展开法[7-8]，F展开法[9-17]等．这些推广的方法都是通过用一个辅助方程的解来替代双曲正切函数法中的双曲正切函数来实现的，这表明如果选择不同的辅助方程就可以得到非线性发展方程不同的精确解．但这种方法以选取的辅助方程能够引出新的孤立波解为前提，故问题的关键在于如何选取合适的辅助方程． 注意到以上所利用的辅助方程一般都是常系数的，对于变系数的辅助方程很少有作者进行研究．本文在Bernoulli辅助方程的基础上做了进一步的推广，把常系数的Bernoulli辅助方程改进为变系数的，并利用它的解给出非线性发展方程的精确解．由于辅助方程的变系数特点，故利用改进的变系数Bernoulli辅助方程可以得到非线性发展方程较为丰富的精确解．

反应扩散方程是非常重要且应用广泛的一类偏微分方程，它描述了生物学中物种数量的迁徙变化，人体或动物等复杂的组织发育形成的过程，人体生理学中的种种现象以及许多有趣的化学反应，具有强烈的实际意义．一类反应扩散方程

ut-uxx-u(1-u)(u-a)=0

(1)

就是一种简单形式的Fitzhugh-Nagumo反应扩散方程，其中f(u)=u(1-u)(u-a)称为扩散源．在生物学中，此方程是一类描述神经再生及传播的演化方程，由该方程可推演出铌(Nb)分子的性质；该方程还从生物现象学的角度就肌球蛋白分子球形部分Ⅱ的行为给予描述[18]．该方程不仅应用在生物群体动力学领域，还广泛出现在生化反应的文献中．因此，研究Fitzhugh-Nagumo方程的精确解在理论和应用方面都具有重要意义．

本文主要利用变系数Bernoulli辅助方程法，并借助数学符号软件Mathematica，给出了方程(1)新的显式精确解，其中包括一般形式的行波解、扭状正则孤立波解和奇异孤立波解．

1 变系数Bernoulli辅助方程法

假设给定一个(1+1)维非线性偏微分方程

F(u,ux,u1,uxx,uxt,utt,…)=0,

(2)

这里的F是关于u=u(x,t)和它的各阶导数的多项式，其中包含非线性项和最高阶导数项．下面，我们简要地介绍变系数Bernoulli辅助方程法的主要步骤．

第一步：设方程(2)具有行波解

u(x,t)=u(ξ),ξ=kx+ct,

(3)

其中，k和c是待定常数．行波变换(3)把方程(2)转化为关于u=u(ξ)的常微分方程

F(u,u′,u″,…)=0.

(4)

第二步：假设方程(4)的解可以表示为函数ω(ξ)的如下多项式：

(5)

这里的正整数n由平衡方程(4)中的最高阶导数项与非线性项所确定，αi(ξ)(i=0,1,2,…,n)是待定函数，ω(ξ)满足下面的变系数Bernoulli辅助方程：

ω′(ξ)=ω(ξ)+q(ξ)ω2(ξ),

(6)

其中，q(ξ)为关于ξ的单变元函数．

第三步：把式(5)代入方程(4)并考虑变系数Bernoulli辅助方程(6)，合并并整理ωi(ξ)相同次数的项，并令ωi(ξ)的各次系数为0得到关于ai(ξ)(i=0,1,2,…,n),q(ξ),k,c的常微分方程组．

第四步：从第三步得到的常微分方程组中解出ai(ξ)(i=0,1,2,…,n)，q(ξ),k,c,然后便可得到了方程(6)的解ω(ξ)，把方程(6)的解ω(ξ)以及ai(ξ)(i=0,1,2,…,n),q(ξ),k,c代入式(5)，便得到了方程(2)的行波解．

注1 变系数Bernoulli辅助方程(6)的解为

(7)

其中，c1为积分常数．

2 Fitzhugh-Nagumo方程的精确解

设方程(1)具有行波解

u(x,t)=u(ξ),ξ=kx+ct,

(8)

其中，k和c是待定常数．行波变换(8)把方程(1)化为关于u=u(ξ)的常微分方程：

u3(ξ)-au2(ξ)-u2(ξ)+au(ξ)+cu′(ξ)-k2u″(ξ)=0.

(9)

由齐次平衡原则，考虑方程(9)中的最高阶导数项u″(ξ)和非线性项u3(ξ)之间的齐次平衡，可设

u(ξ)=a1(ξ)ω(ξ),a1(ξ)≠0.

(10)

把式(10)代入方程(9)并考虑变系数Bernoulli辅助方程(6)，令ωi(ξ)的系数为0，则得到一个关于a1(ξ),q(ξ),k,c的常微分方程组

ω1: -a1(ξ)k2-2a1′(ξ)k2-a1″(ξ)k2+aa1(ξ)+

ca1(ξ)+ca1′(ξ)=0,

ω2: -3q(ξ)a1(ξ)k2-a1(ξ)q′(ξ)k2-

cq(ξ)a1(ξ)=0,

(11)

由常微分方程组(11)中的ω3可知

(12)

或

(13)

以下分两种情况进行讨论.

情形1 将式(12)代入常微分方程组(11)中的ω2，并化简得：

(14)

求解常微分方程(14)，得：

(15)

其中，c2为积分常数．将式(12)代入常微分方程组(11)中的ω1，并化简得：

aq(ξ)+cq(ξ)+cq′(ξ)-q(ξ)k2-2q′(ξ)k2-q″(ξ)k2=0.

(16)

利用式(15)，求解常微分方程(16)得：

(17)

或

(18)

故由式(17)、(15)、(7)及式(12)，可得方程(1)的精确解：

(19)

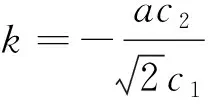
又由式(18)、(15)、(7)及式(12)，可得方程(1)的另一精确解：

(20)

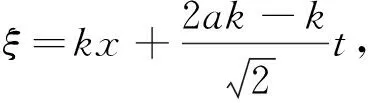
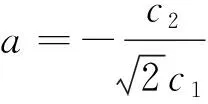
情形2 将式(13)代入常微分方程组(11)中的ω2，并化简得：

(21)

求解常微分方程(21)得：

(22)

其中，c2为积分常数．将式(13)代入常微分方程组(22)中的ω1，并化简得：

aq(ξ)+cq(ξ)+cq′(ξ)-q(ξ)k2-2q′(ξ)k2-q″(ξ)k2=0.

(23)

利用式(22)，求解常微分方程(23)，得：

(24)

或

(25)

故由式(24)、(22)、(7)及式(13)，可得方程(1)的精确解

(26)

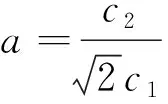
又由式(25)、(22)、(7)及式(13)，可得方程(1)的另一精确解

(27)

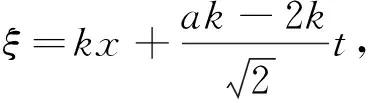
取波数时，方程(1)有奇异孤立波解

注2 在变系数Bernoulli辅助方程法中，辅助方程的变系数q(ξ)是未知的函数，需要由常微分方程组确定．在这一点上，本文所采用的方法同其他的展开法有所不同．

注3 若取变系数Bernoulli辅助方程为：

ω′(ξ)=p(ξ)ω(ξ)+ω2(ξ),

(28)

其中，p(ξ)为关于ξ的单变元函数．类似地，可得到方程(1)的四组精确解

(29)

(30)

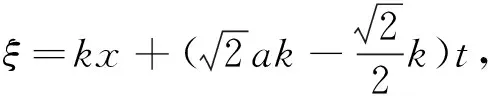
(31)

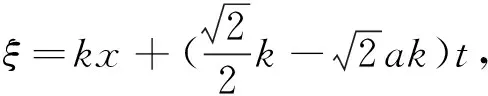
(32)

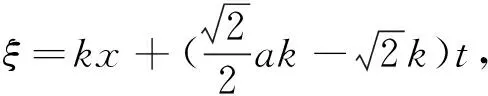
对于方程(1)的解(29)～(32)，取波数为特定值，同样可以得到相应的孤立波解．由于篇幅限制，这里从略．

参考文献：

[1] WANG M L. Solitary wave solutions for variant Boussinesq equations[J]. Phys切 Lett, 1995(A199):169-172.

[2] PARKES E J, DUFFY B R. An automated tanh-function method for finding solitary wave solutions to nonlinear evolution equations[J]. Comput. Phys Commun, 1996(98):288-300.

[3] 闫振亚，张鸿庆. 具有三个任意函数的变系数KdV- MKdV方程的精确孤子解[J]. 物理学报，1999, 48 (11): 1957-1961.

[4] YAN C. A simple transformation for nonlinear waves[J]. Phys Lett, 1996(A244):77-84.

[5] FAN E G. Extended tanh-function method and its applications to nonlinear equations[J]. Phys Lett, 2000(A277): 211-218.

[6] ELWAKIL S A, ELLABANY S K, ZAHARAN M A, et al. Modified extended tanh-function method for solving nonlinear partial differential equations[J]. Phys Lett, 2002(A299): 179-188.

[7] PARKES E J, DUFFY B R, ABBOTT P C. The Jacobi elliptic-function method for finding periodic-wave solutions to nonlinear evolution equations[J]. Phys Lett, 2001(A295):280-286.

[8] LIU S K, FU Z T, LIU S D, et al. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations[J]. Phys Lett, 2001(A289):69-74.

[9] ZhOU Y B, WANG M L, WANG Y M. Periodic wave solutions to a coupled KdV equations with variable coefficients [J]. Phys Lett, 2003(A308):31-36.

[10]WANG M L, ZHOU Y B. The periodic wave solutions for the Klein-Gordon-Schrdinger equations[J]. Phys Lett, 2003(A318):84-92.

[11]李向正, 张金良, 王跃明,等. 非线性Schdinger方程的包络波解[J]. 物理学报, 2004, 53(12):4045-4051.

[12]WANG M L, LI X Z. Applications of F-expansion to periodic wave solutions for a new Hamiltonian amplitude equation[J]. Chaos, Solitons and Fractals, 2005, 24(6): 1257-1268.

[13]WANG M L, LI X Z. Exact solutions to double Sine- Gordon equation[J]. Chaos, Solitons and Fractals, 2006, 27(2): 477-486.

[14]ZHANG J L, WANG M L, LI X Z. Solitary waves for Cubic-Quintic nonlinear Schrdinger equation with variable coefficients[J]. Commun Theor Phys, 2006, 45(2): 343-346.

[15]LIX Z, WANG M L. A sub-ODE method for finding exact solutions of a generalized KdV-mKdV equation with high-order nonlinear terms[J]. Phys Lett, 2007(A361):115-118.

[16]WANG D S, LIU Y F, ZhANG H Q. Symbolic computation and families of Jacobi elliptic function solutions of the (2+1)-dimensional Nizhnik-Novikov-Veselov equation [J]. Appl Math Comput， 2005(168): 823-847.

[17]ZhANG J F, DAI C Q, YANG Q, et al. Variable- coefficient F-expansion method and its application to nonlinear Schrdinger equation[J]. Opt Commun, 2005(252):408-421.

[18]WAZ A M. Analytic study on Burgers, Fisher, Huxley equations and combined forms of these equations[J]. Appl Math Comput, 2008(195):754-761.