基于机器视觉的智能化布匹瑕疵检测方法

李 鑫，王新莉，赵让乾，吴素珍

(河南工程学院 机械工程系，河南 郑州 451191)

布匹瑕疵检测是纺织品质量控制和管理的主要环节之一.长期以来，国内大多数的织布厂主要依靠人工进行检测.这种传统的检测方法不仅速度慢、劳动强度大，而且易受人为因素的影响，误检率和漏检率高.为了解决这些问题，近年来基于机器视觉的瑕疵检测方法备受关注.

1 检测原理概述

纹理是布匹的重要特征，纹理分析是采用机器视觉对布匹进行瑕疵检测的重要内容.常用的纹理表达和描述方法主要有4种：统计法、结构法、频谱法和时频域变换法.为了满足在线检测的实时性要求，本文将统计法与时频域变换的方法相结合，提出了一种智能化的布匹瑕疵检测方法.

统计法是一种借助灰度直方图的矩来描述纹理，利用求取到的统计特征量(如标准差)找到疵点的检测方法.这种方法简单易行，但对图像质量的要求较高，易受噪声的影响.

时频域变换法，是将图像信息分解到各子域，再分析抑制图像纹理的信息频段，从而增强疵点信息频段，完成检测，如Gabor变换、小波变换等.

为了提高检测速度，先对图像进行初检测.将图像分成大小相等的局部窗口，计算每个窗口的标准差及灰度平均值，将其与无瑕疵图像的平均标准差及灰度平均值相比较，从而确定待检测图像有无瑕疵及瑕疵的大致区域.然后，采用一种基于Gabor滤波器的检测方法对有瑕疵的区域进行精确检测，确定其位置及大小.该方法是一种通过提取布匹在不同尺度不同方向的纹理特征，进而滤去纹理突出瑕疵(非纹理部分)的检测方法.

2 相关理论

2．1 标准差及灰度平均值

标准差是一个用来反映数值相对于平均值离散程度的统计量.对于一幅不含疵点的布匹图像而言，图像的纹理特征是确定的，若将其等分成若干子窗口，简称子块，那么各子块的标准差和灰度平均值应该大小接近，在小范围内波动.当疵点出现时，图像的纹理特征遭到破坏，疵点附近的灰度值一定会发生较大变化，其标准差和灰度平均值都会超出正常的范围，从而检测出疵点的存在.

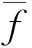
(1)

则其标准差δ为：

(2)

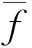
2．2 Gabor滤波器

Gabor变换的基本函数具有与人类视觉基元相似的性质，也是唯一能够达到时频测不准下界的函数，这些特点对于研究图像特征检测或空间频率滤波是极其重要的.

Gabor变换由STFT发展而来， 2D-Gabor函数由一均值为0的Gauss函数和一个给定方向和频率的复变正弦波函数调制而成，其中高斯包络提供空域定位能力，弦波函数则提供频域分析能力.二维的Gabor函数表达式：

(3)

其中，g(x,y)是特殊情况下的Gabor函数，它的高斯函数具有环形对称性，与正弦项的相位差为0，以原点为中心.ejwx是沿x轴的复变正弦波.上述表达式可以写作：

Gabor(x，y)=GaborR(x，y)+jGaborl(x,y).

(4)

将Gabor(x,y)中的x, y坐标以θ角度进行方向坐标变换：

x′=x·cosθ+y·sinθ，

y′=-x·sinθ+y·cosθ，

可得Gabor函数的实部为：

(5)

Gabor函数的虚部为：

(6)

其中，f0是频带的中心频率，θ是方向角，σ决定了通过频率的带宽，这些参数决定了Gabor函数在空域和频域中的位置.

本文中，θ选择0°， 45°， 90°和135°，分别建立这4个方向上的二维Gabor滤波器的实部和虚部模板，用这些模板对图像进行卷积运算便得到处理结果的实部和虚部，两者的和即为图像的最终处理结果.

3 瑕疵检测算法

3．1 利用标准差及灰度平均值进行初检测

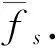
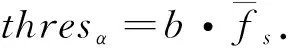
3．2 建立图像的金字塔模型

初检测后，瑕疵所在的大致区域已经确定，接着在该区域采用一种基于Gabor滤波器的检测方法就可完成对瑕疵的精确检测.

纹理与尺度有密切联系，一般仅在一定的尺度上可以观察到.因此，要分析纹理需要确定一定的尺度.利用多分辨率技术检测纹理，是获得理想瑕疵检测的好途径.在本文中，对布匹瑕疵检测使用多分辨率的过程转化为建立金字塔结构的过程.通过将频域中以45°为步长旋转并对频率在空间域内减半采样，就可以建立金字塔模型.

由于原始坯布是按照经纬向规律织成的，在对角方向也有明显的纹理特征，所以在实践中仅采用水平和垂直两个方向进行滤波.基于图像大小规范化和计算代价的考虑，在算法实现时采用4层金字塔结构，每层包含两幅图像，分别代表布匹在0°和90°方向上的特性.求取下一层金字塔原始图像，对上一层原始图像进行数据缩减采样之前，要对其进行一次低通滤波，以消除高频噪声的影响.建立金字塔模型的步骤如下：

(1) 采集的原始图像作为金字塔的第0层；

(2) 对每层的原始图像在0°和90°两个方向上进行Gabor滤波；

(3) 与步骤(2)同时，对该层原始图像进行低通滤波；

(4) 对步骤(3)得到的图像减半采样，从而获得金字塔下一层的原始图像；

(5) 返回步骤(2)，继续操作，直到生成4层(0～3)建立金字塔模型，将第3层(最高层)的低通滤波结果保存为tlpr.

至此，描述了纹理在8个方向上的特征，下面进行二值化操作，对纹理进行滤除.

首先，获取各通道图像的对比图.将得到的各通道图像都除以第3层图像的原始图像tlpr,即：

Tpq(x，y)=tpq(x，y)/tlpr(x，y)，

(7)

式中，p=0，1，2，3是金字塔的层数，q=0，1分别代表水平和垂直两个方向.

同理得到的无瑕疵模板各通道对比图Rpq(x，y)，

即：

Rpq(x，y)=rpq(x，y)/rlpr(x，y).

(8)

其次，获得待检测图像与无瑕疵模板对比图.将上步获得的待检测图像与无瑕疵模板的像素灰度平均值相减，并取绝对值，即：

(9)

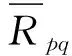
(10)

M,N分别为输入的原始图像的行数和列数.

最后，对得到的图像进行二值化.为了消除噪声，以εδpq为阈值对上步得到的各通道图像进行二值化 .

(11)

其中，ε为常数，它的值越小，检测精度越高，但是瑕疵误报的可能性越大.本系统中取ε=2.δpq为无瑕疵模板的像素灰度的标准差，即：

(12)

至此，就获得了8个通道下的滤波结果，建立了图像的金字塔模型.这部分算法的流程如图1所示.

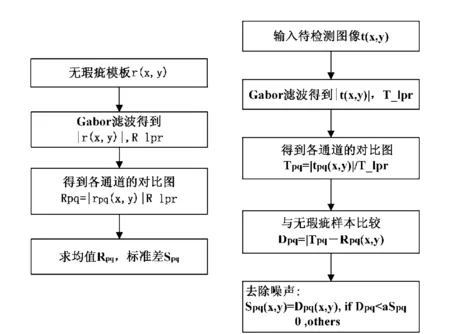
图1 建立金字塔模型算法流程图Fig.1 Flowchart of establishing pyramid model

3．3 图像融合

建立的金字塔模型是原图像在不同分辨率、不同方向上的处理结果.但是，这8通道的处理结果都只侧重于布匹纹理的一个方面，不够全面.若据此判断，会带来较大的误报可能.所以，必须对所有图像反映的信息进行合理的综合，就是要进行图像融合.按一定的算法对这8通道的图像进行叠加，得到的最终的融合图像可以体现出不同频率不同方向下瑕疵呈现出的纹理和形状特征.

逻辑滤波器法是最直观的在空间域进行的像素级图像融合方法，即将两个像素的值进行逻辑运算.本文采用这种方法对获得的8通道图像进行了融合.步骤如下：

(1)层内融合.对金字塔每层内各个方向上的图像进行叠加，即对应像素的逻辑或操作；

(2)层间融合.对相邻层图像像素进行叠加，即采用逻辑与操作，得到P01,P12,P23；

(3)对上步得到的图像采取或操作，进行最终融合，得到图像P.

经过上述操作得到的二值化图像经常会含有噪声引起的斑点.为了解决这个问题，我们对图像进行形态处理.

腐蚀与膨胀是最基本的形态处理.腐蚀处理能够将粘连的目标物进行分离，膨胀处理可以将断开的目标物进行连接，但是经过这两种处理后，目标物的面积都会发生改变.因此，在本文中对融合得到的图像进行开运算，即使用一个结构元素对图像先腐蚀再进行膨胀的运算.

R=P·S=(PΘS)⊕S，

(13)

式中，P为融合后得到的二值化图像，S为结构元素.通过开运算，在基本保持目标原有大小不变的情况下，去除了小颗粒噪声，得到最终的结果图像R.

4 实验结果

为了对上述算法进行验证，本文选用纹理均匀的蓝布.输入的图像大小为384×384， 256级灰度.对于瑕疵样本1，初检测中，根据阈值thresδ=3.810 4和thresa=83.751 4对原始图像进行第一次处理，可得Bi2(1，2……11，12)子块为有瑕疵区域，再经过Gabor滤波检测，即可得到图2的处理结果.同理，对瑕疵样本2进行处理，结果如图3所示.

依据得到的处理结果，用户即可对瑕疵进行定位并确定其大小.实践证明，这种检测方法速度快，准确率高，具有良好的检测效果.

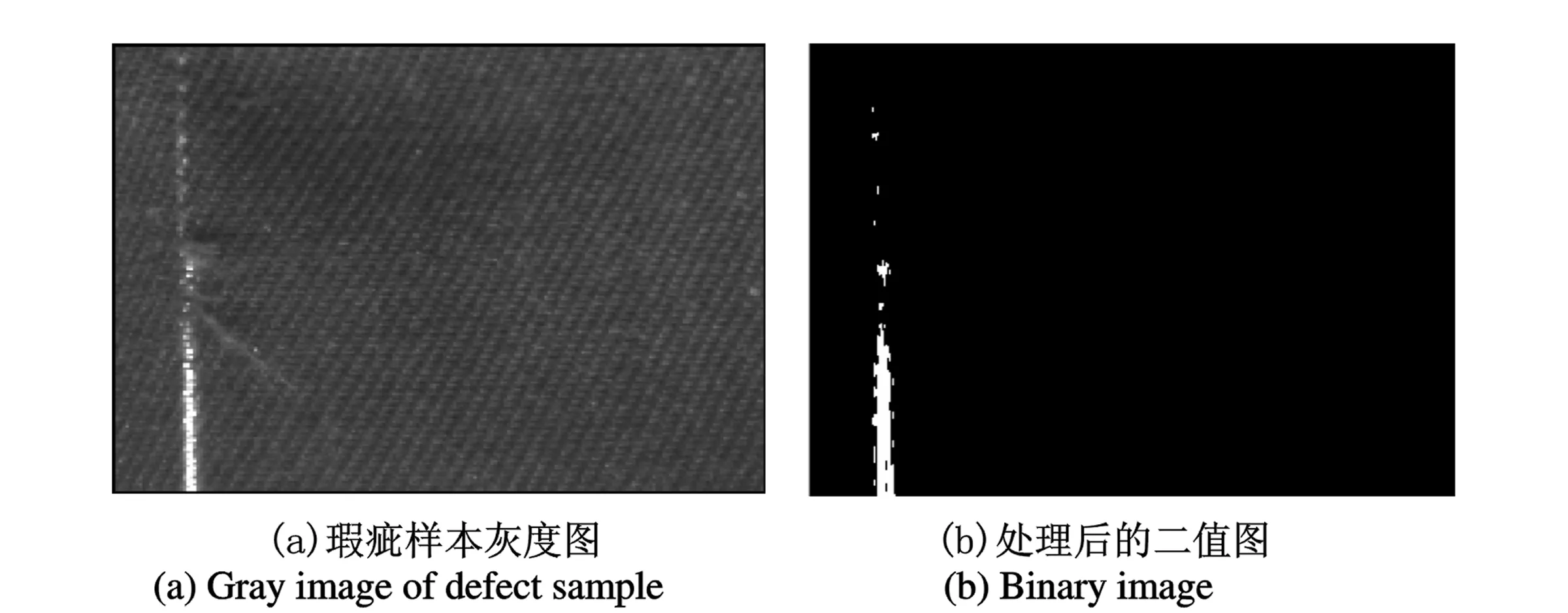
图2 瑕疵样本1检测结果Fig. 2 Detection result of defect sample 1

图3 瑕疵样本2检测结果Fig.3 Detection result of defect sample 2

参考文献:

[1] ESCOFET，NAVARRO. Detection of local defects in textile webs using Gabor filter[J].SPIE,1996(2785):163-170.

[2] 张轶.实时布匹瑕疵检测技术研究[D].天津:天津工业大学，2004.

[3] 肖乐，朱玉文,丁丽宏,等.基于Gabor滤波器的布匹瑕疵自动检测方法[J].北京理工大学学报，2002(6)：718-721.

[4] 曾姝彦，张广军，李秀智.基于Gabor滤波器的图像目标识别方法[J].北京航空航天大学学报，2006(8):954-957.

[5] 章毓晋.图像分析[M].2版.北京：清华大学出版社，2005：279-298.

[6] 朱虹.数字图像处理基础[M].北京：科学出版社，2005:154-161.

[7] 夏明革,何友,唐小明,等.像素级图像融合方法分类与比较[J].火力与指挥控制，2002，27(3)：161-164.

[8] 卿湘运，段红，魏俊民.基于局部熵的织物疵点检测与识别的研究[J].纺织学报，2004，25(5)：57-59.

[9] 努尔顿，左保齐.织物疵点智能化判别[J].丝绸，2003(11)：28-30.