区间值狄里克莱级数及其收敛域
段 玉
(湖南商学院信息学院,中国 长沙 410000)
狄里克莱级数是在19世纪中L· 狄里克莱研究数论时引进的.它可看作是泰勒级数的推广,也是拉普拉斯—斯蒂尔杰斯变换的一个特例.很多学者分别对狄里克莱级数与区间值函数项级数进行了一系列的研究.如:余家荣[1]研究随机狄里克莱级数的a.s.(几乎必然)收敛性和在a.s.收敛半平面内的a.s.增长性;为此,还研究了狄里克莱级数在收敛半平面内的增长性,推进了Valiron G.和Arnold L.的有关结果.马生全[2-3](2000~2002年)研究了复区间值函数与复模糊值函数的一致收敛性;郭志林[4](2005年)研究了区间值函数项级数一致收敛的概念和判别方法,给出了一致收敛性的区间值函数项级数的分析性质;其他请参考文献[5~7].到目前为止,还没有关于区间值狄里克莱级数的研究.本文试图引入区间值狄里克莱级数有关概念,并得到区间值狄里克莱级数的绝对收敛与一致收敛的有关定理.
1 预备知识
记R为实数域,C为复数域,C0⊂C
定义1称a=[al,au]={x|al≤x≤au}为一个区间数,al与au分别为区间数的下限(左端点)和上限(右端点),当al=au时,区间退化为一个实数.
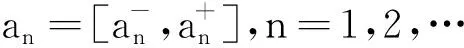
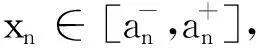
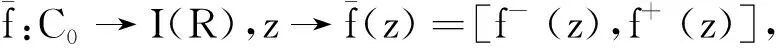
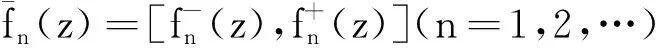
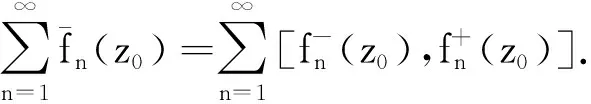
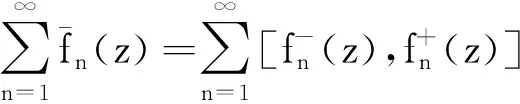
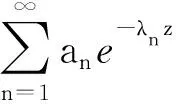
2 区间值狄里克莱级数
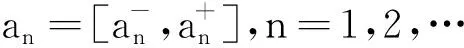
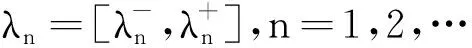
显然,区间值狄里克莱级数是一种特殊的区间值复函数项级数.
3 有关结论
3.1 系数区间值狄里克莱级数的收敛性
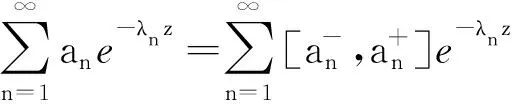
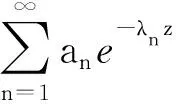
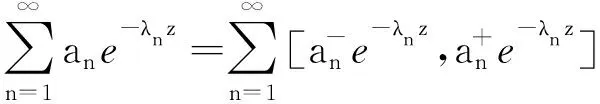
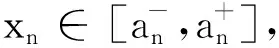
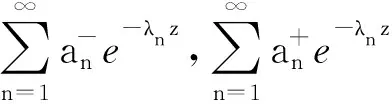
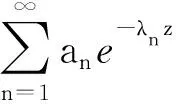
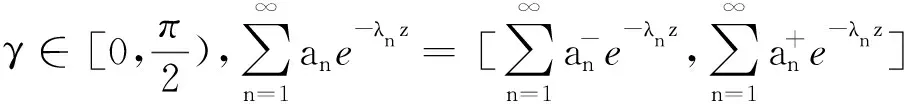
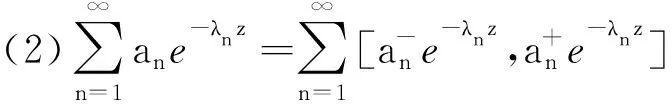
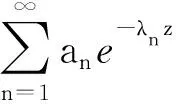
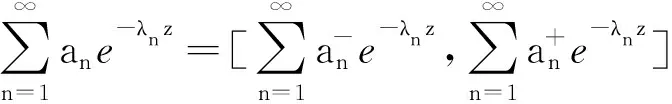
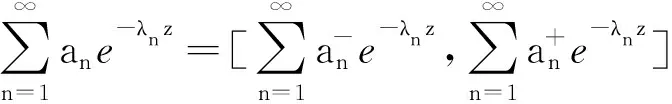
(2) 同理,应用文献[1]定理1.2 (2)可证(2)(证明略).
3.2 指数区间值狄里克莱级数的收敛性
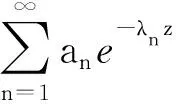
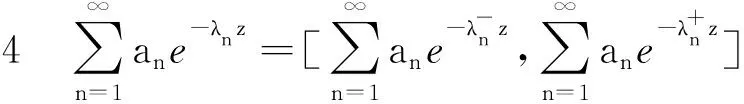
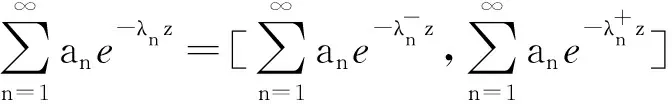
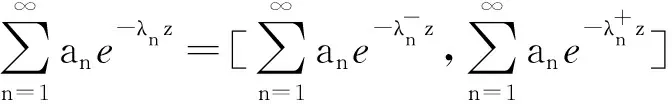
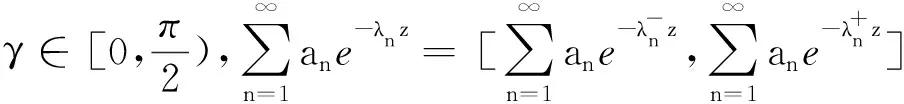

证明与定理2相似(略).
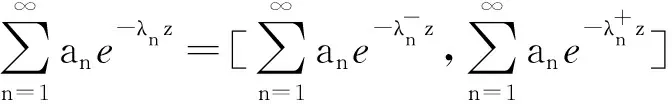
证(1)的证明参见定理3(1)的证明;
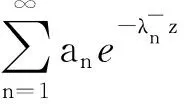
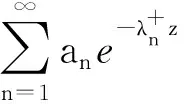
参考文献:
[1] 余家荣.狄里克莱级数与随机狄里克莱级数[M].北京:科学出版社,1997.
[2] 马生全.复区间值函数与复模糊值函数的一致收敛性[J].辽宁工程技术大学学报,2001,(10):615-617.
[3] 马生全.模糊复分析[M].北京:民族出版社,2001.
[4] 郭志林.Fuzzy区间值函数项级数及其一致收敛性[J].广西右江民族师专学报,2005,(6):9-10.
[5] 周礼刚,陈华友.两类区间数判断矩阵的一致性研究[J].运筹与管理,2008,(8):48-49.
[6] 武进贵,郭志林.实Fuzzy数项级数及其收敛性[J].百色学院学报, 2006,(3):10-12.
[7] 何 波,郭嗣琮,孟 毅. 结构元线性生成的模糊数列极限与级数收敛性[J].科学技术与工程, 2005,(15):1 055-1 056.

