基于因子和聚类分析的城镇居民家庭消费性支出应用研究
冯建中,何先平
(长江大学信息与数学学院,湖北 荆州 434023)
基于因子和聚类分析的城镇居民家庭消费性支出应用研究
冯建中,何先平
(长江大学信息与数学学院,湖北 荆州 434023)
以2007年全国31个地区城镇居民家庭消费性支出数据作为样本,建立了消费性支出评价指标体系,运用因子分析法进行分析,提取出3个主因子,然后利用聚类分析对各地区进行了分类。
消费性支出;因子分析;聚类分析
消费是指人们为了满足生活需要,对物质产品的消耗和享受服务的行为过程。随着近几年我国社会和经济的发展,城镇居民消费水平不断提高,消费结构发生了显著变化。而且作为社会总需求最重要的组成部分,居民的消费增长直接影响到整个国民经济增长的速度和质量。国内外对居民消费增长问题的研究由来已久,其中对消费结构变化的研究已成为近年来学者们研究的热点[1]。但目前关于消费结构的研究多集中在其变动趋势方面,消费性支出的地区性横向比较分析[2]则相对较少。而对我国来说各地区的经济发展不平衡,居民的消费水平和消费性支出也存在着很大的差异。因此,对我国各地区城镇居民人均消费性支出的各项指标进行统计分析,明确我国居民的消费性支出差异的数量特质,就显得尤为必要。
1 评价指标体系的建立
要对城镇居民消费性支出水平进行准确的描述,必须构建合适的指标体系。指标体系的构建必须遵循以下原则:全面性原则、整合性原则、代表性原则和实际可操作原则。在总结相关研究成果的基础上,遵循以上原则,本研究建立了如下指标体系(单位:元):食品X1、衣着X2、居住X3、家庭设备用品及服务X4、医疗保健X5、交通和通信X6、教育文化娱乐服务X7、杂项商品和服务X8。数据来源于《中国统计年鉴2008》[3]。
2 因子分析模型及其步骤
因子分析的数学模型为:
X=AF+ε
式中,X=(X1,X2,…,Xp)′为原指标,F=(F1,F2,…,Fm)′为X的公共因子,A为因子载荷矩阵,ε为特殊因子。
本研究使用的因子分析步骤如下[4]:(1)将原始数据标准化,仍记为X;(2)建立相关系数矩阵R;(3)解特征方程|R-λE|=0,计算特征值和特征向量,当累计贡献率不少于85%时,取前k个主成分代替原来的m个指标,计算因子载荷矩阵A;(4)对A进行最大正交旋转变换;(5)对主因子进行命名和解释。如需进行排序,则计算各个主因子的得分Fi=αix,以贡献率为权重,对Fi加权计算综合因子得分。
2.1 数据分析

表1 相关系数矩阵特征值与方差贡献率Table 1 The eigenvalues of correlation coefficient matrix and contribution rate of variance
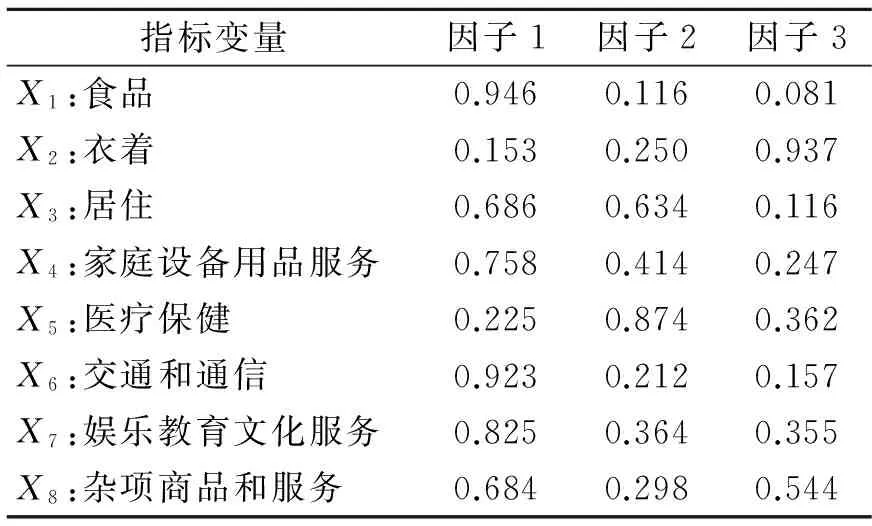
表2 旋转后的因子载荷矩阵Table 2 Rotated factor pattern matrix
对原始数据进行标准化以消除指标间不同量纲对分析结果的影响,建立指标间的相关系数矩阵R,计算其特征值和累计贡献率[5],前3个特征值及其贡献率如表1所示。由表1可见,前3个特征值的方差累计贡献率已经达到90.406%,信息损失仅为9.594%,取前3个特征值建立因子载荷矩阵。由于初始因子载荷矩阵结构不够简明,各因子的含义不够突出。为此采用方差最大正交旋转变换,使各变量在某些因子上产生较高载荷,而在其余因子上载荷较小,从而得到旋转后的因子载荷矩阵,如表2所示。
2.2 因子命名及解释
根据表2将指标分为3类,第一个主因子在X1(食品)、X3(居住)、X4(家庭设备用品及服务)、X6(交通和通信)、X7(教育文化娱乐服务)、X8(杂项商品和服务)上载荷比较大,特别是在X1、X6、X7上更为明显,这个因子主要体现了城镇居民消费性支出的整体水平及日常消费中占主导地位的食品消费,是衡量消费性支出水平的最主要因子,因此可以定义其为基本生活因子。第二个主因子在X5(医疗保健)上具有较大载荷,称之为健康投资因子。第三个主因子在X2(衣着)上具有较大载荷,称之为衣着消费因子。
2.3 标准因子得分函数模型
根据SPSS程序运行结果,得到标准因子得分函数模型为:
F1=0.404X1-0.165X2+0.044X3+0.157X4-0.322X5+0.34X6+0.198X7+0.131X8
F2=0.296X1-0.272X2+0.545X3+0.118X4-0.945X5+0.192X6-0.5X7-0.198X8
F3=0.106X1-0.945X2+0.34X3+0.062X4-0.128X5-0.07X6+0.089X7+0.374X8
利用该模型可以计算从不同角度反映各地区城镇居民消费性支出的水平。再以3个主成分对应的方差贡献率为权数计算综合分值,得分只代表在构建的指标下各地区的相对差别。综合得分公式为:
F=0.7883F1+0.1422F2+0.07F3
用该公式计算各地区的综合分值,可以排序出2007年我国31个地区城镇居民消费性支出水平的高低,结果见表3。
根据表3中各地区主因子得分数据,采用系统聚类法进行聚类分析,根据得到的聚类谱系图,31个地区被分为3类的最终结果如下:
第一类:北京、上海、浙江、广东。
第二类:天津、江苏、福建。
第三类:河北、山西、内蒙古、辽宁、吉林、黑龙江、安徽、江西、山东、河南、湖北、湖南、广西、海南、重庆、四川、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆。
3 结果分析
首先,随着我国经济的迅速发展,各地区在消费性支出方面都有了较大幅度的提高,我国的城镇居民人均消费性支出也由2002年的6 029.88元增长到2007年的9 997.47元,增幅在65%以上。但是,就反映食品、居住、家庭设备用品及服务、交通和通信、教育文化娱乐服务、杂项商品和服务的基本生活因子F1而言,我国31个地区综合消费水平发展极不平衡,存在较大的差异。得分最高的上海和得分最低的黑龙江相差4.3分,并且只有上海、广东、浙江、北京、福建、江苏、海南、天津、广西、四川、西藏11个地区得分在0分以上,其余2/3的地区得分都小于0,这与我国各地区整体经济发展水平的实际情况吻合,说明大部分地区还处于全国消费平均水平之下,有待进一步提高和引导消费。为此,对于那些F1得分小于0的地区,只有大力发展经济,使得大家的可支配收入水平提高,才能有效地扩大内需,拉动消费。

表3 各地区因子得分和综合测评得分及排序Table 3 Factor and comprehensive assessment score of every area and sequence
其次,从健康投资因子F2和衣着消费因子F3的得分来看,各地区的排序变化相对比F1要大得多。如辽宁、山西、河北、吉林、黑龙江较之前的得分,名次分别上升了16、19、26、26和22位;而上海、四川和西藏较之前的得分名次分别下降了24、19、20位,这与各地区城镇居民的消费观念、所处地理位置和条件以及民族习惯有着很大的关系。F2得分靠前的天津、北京、河北和吉林等地区,居民的健康投资意识较强,其医疗保健等卫生条件也相对较好;而西藏、贵州、江西等地区的F2得分较低,可能是当地经济发展制约或所处地理环境较为恶劣所引起的。对于衣着消费因子F3随意性可能稍微大点,可能与经济发展水平、消费习惯以及民族原因有关,如得分前5位分别是内蒙古、北京、浙江、上海和新疆就可以看出端倪。
最后,从因子总得分F值来看,得分超过0分(全国平均水平)的仅有8个地区,74.2%的地区在全国平均水平之下,这说明我国各地区城镇居民的消费结果差异很大,消费性支出水平发展很不平衡。根据F值排序,可以把我国31个地区分为3类:第一类是Fgt;1,包括上海、广东、北京、浙江,属于经济较发达地区,其消费性支出的综合测评得分远远高于其它地区;第二类是0lt;Flt;1,包括福建、天津、海南、江苏,属于中等消费水平地区;第三类是Flt;0,包括其余的23个地区,属于消费水平较低地区。
另外,从因子分析和聚类分析的结果可以看出,各地区综合测评得分与聚类结果基本一致,这也充分说明把因子分析法应用到多指标城镇居民消费性支出水平评价中是成功的,所得结果客观、可信。
4 结束语
整体上来看,尽管受到就业压力加大等不利因素的影响,但由于扩大内需、刺激消费等多重政策的实施,2007年我国各地区城镇居民消费继续保持良好增长态势[6]。从消费结构看,基本生存消费(如食品、居住、家庭设备用品及服务、杂项商品和服务)比重下降,享受和服务型需求(如衣着、医疗保健、交通和通信、教育文化娱乐服务)比重上升。我国各地区城镇居民的消费结构差异很大,消费性支出水平发展很不平衡,很多地区的消费水平和消费结构都有待进一步的提高。
[1]孙彩虹.我国城镇居民消费结构变动的因子分析[J].重庆工商大学学报(西部论坛),2007,(1):103~105.
[2]余明江,季 丽,胡云霞.我国城镇居民消费性支出的因子分析[J].安徽工业大学学报,2008,25(2):221~225.
[3]中华人民共和国国家统计局.中国统计年鉴·2008[M].北京:中国统计出版社.2009.
[4]王庆丰,党耀国,王丽敏.基于因子分析和聚类分析的县域经济发展研究——以河南省18个县(市)为例[J].数理统计与管理,2009,28(3):495~501.
[5]卢纹岱.Spss for Windows统计分析 [M].北京:电子工业出版社,2002.311~315.
[6]祁京梅.2007年消费形势分析和2008年走势预测[EB/OL].http://www.china.com.cn/economic/zhuanti/08jjbg/2008-01/23/content_9575705.htm,2008-01-23.
2009-11-04
冯建中(1980—),男,河南正阳人,理学硕士,讲师,研究方向为高等数理统计.
10.3969/j.issn.1673-1409(S).2010.01.025
F126.1
A
1673-1409(2010)01-S097-04
——“习作单元”阅读文的教学指向

