混沌量化算法研究及测试分析
唐立法,周健勇,董斌辉,郭磊芳
(上海理工大学 管理学院,上海 200093)
自Matthews在1989年首次将混沌用于密码学研究以来,混沌已经应用到数据加密、数字水印、图像加密等信息安全各个方面,并得到了广泛的研究和发展。由于混沌在信息安全中的应用都是要利用混沌系统的随机特性,大都体现在通过量化后的随机序列的性能上,因此生成随机序列的随机性将直接影响到系统的安全性,所以混沌量化是其应用的第一步,也是最关键一步。本文从混沌量化算法的原理入手,分析与比较当前主要的混沌量化算法,通过相关检验比较各种算法的优劣,最后从生成密码学安全的伪随机角度,在对现有算法的分析和测试数据的基础上提出一种改进的量化算法。
1 混沌量化原理
在混沌密码研究中,目前并没有关于混沌量化的标准定义,混沌序列量化后的序列也称之为混沌伪随机序列,本文采用文献[1]中的数字混沌定义得到混沌量化的定义。混沌量化就是将实数的混沌序列量化转换为特定的一组符号序列。
定义1:令Xd为一个有限集合,Fd为一个定义在Xd上 的 自 映 射 , 即 Fd:Xd→Xd, 则 xn+1=F(xn),x0∈Xd,n=0,1,2,3…称为有限域上的迭代映射。
定义2:设F为一个定义在连续相空间X上的混沌映射,则按下面数字化方法获得的有限域上的迭代映射Fd称为数字混沌映射:取一个有限的分割 β={C0,C1,…,Cm-1}覆盖相空间 X,将 F:X→X 用 Fd:Xd→Xd代替,此处Xd={0,1,2,…,m-1}。将数字化后的混沌映射称为数字混沌,而类似上述将实数序列转化为整数序列(或比特位)的过程称为混沌量化。
2 常见的混沌量化算法及测试分析
2.1 常见的混沌量化算法
自混沌应用于信息安全以来,混沌量化虽然是混沌应用的必须过程,但只是作为一个辅助手段来对混沌序列加以利用,大量文献设计的基于混沌的安全系统都随意地采用量化方法。由于现有量化算法有限,且大多数方法在原理上类似,各种量化方法的量化效率不清楚,给实际应用带来了很大的安全隐患。下面是一些常见的一维Logistic混沌系统量化算法(可以推广到其他多维混沌系统),混沌系统在混沌区内输出的时间序列为{xn}。
(1)实数值序列,混沌迭代直接形成的序列,这种方法的序列不宜直接用于加密,而且理论研究已经表明[2],直接采用原始混沌序列作为密钥的平凡混沌加密是可破解的。因此,该方法极不安全,一般不予采用。
(2)二值量化,又称二次粗粒化方法[3]。该方法也是最常见的量化方法之一,主要是定义一个阙值μ*,然后将{xn}量化得到 0、1组成的符号序列{yn},量化函数如下:

(3)位序列设计[4,5]。该方法是把混沌实数值序列转化为一定长度的浮点数形式而得到:

其中 yi(xk)∈{0,1}是 xk的第 i位,所需的序列即为{yn},这样混沌系统每迭代一次就可以得到长为L比特的二值序列。对于每个混沌实数值转化成的二值序列还可以作部分变化,只从中抽取部分序列,不仅随机性得到提高,同时也提高了密钥强度。上述是针对(0,1)区间的情况,可以推广到普遍情况下的生成位序列方法[6]。
(4)多次粗粒化。可以分为等分区间和不等分区间两类。其实质是将相空间进行分割,然后与给定符号序列进行关联。给定一个由m个符号组成的符号集合S={s0,s1,…,sm-1}和一个 m+1个临界点组成的集合 R={R0,R1,…,Rm},用下列转换函数将时间序列{xn}转化为符号序列{yn}:

(5)整数求余量化。是指从实数值混沌序列中利用抽取函数取出若干位有效数字构成整数,并对此整数求余,一般是对256求余,生成一个0~255内的整数,便于加密时使用。
上述是常见的一维混沌量化的相关方法,每一种都可以推广到高维混沌系统。当然由于高维混沌系统特有的性质,也有其他的量化方法,如文献[7]就采用混沌吸引子分区的方式来量化二维Henon混沌系统。
2.2 混沌量化方法的比较研究
由于混沌安全系统主要是利用混沌系统的随机性能,有的甚至直接将量化序列作为相关密钥使用,因此量化后序列的随机性是衡量量化算法优劣的主要指标之一。对于上面常见的五类量化算法,本文选取其中两种典型方法:二值量化和等分区间多次粗粒化。下面测试采用的混沌系统为Logistic混沌映射,将分别采用谱测试和FIPS140-2对随机数进行标准测试。由于Logistic混沌系统在系统参数μ0=4.0时产生的序列随机性要好于其他参数值,为了测试混沌系统参数带来的影响,同时测试了μ0取不同值时的情况。
(1)二维谱测试
这是目前一种常用的直观的测试方法,它在综合检验和评价随机数序列的质量方面有其独特的优点。二维谱测试将随机数序列的相邻元素组成重叠对(二维矢量),将它们标绘在相应的平面区间上,构成散点图。根据散点图中点的分布,可以直观地判断随机数序列分布及相关特征。如果一个随机数序列缺乏均匀性,很容易地从散点图观察到。本文分别采用选定的两种量化算法对Logistic混沌序列进行量化,将量化后序列依次组合成0~255内的整数,并将相邻的元素组成二维矢量,绘制在的平面区间上。二维谱测试的点分布图如图1。
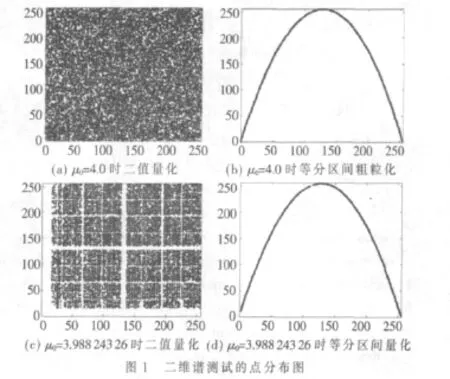
从上述散点图可以看出,当参数μ0=4.0时,二值量化比较均匀地分布在平面区间上,但是多次粗粒化却呈现很强的规律性。这是由于Logistic混沌方程相邻两点具有比较固定的迭代关系造成的。而呈现抛物线是由于等分区间粗粒化没有考虑方程中概率密度的关系造成的,虽然从一定程度上反映了多次粗粒化的缺点,但是其序列的其他性质还有待检验。而当参数μ0减小很少时,两种量化方法都出现了明显的改变。虽然图1(d)与图1(b)在形状上大致相同,但此时粗粒化量化效果更差。而二值量化出现了明显的断裂与分块,量化后的随机性出现明显的下降。因此二值量化算法在μ0=4.0时才具有较好的量化效果,而多次粗粒化由于混沌系统本身和测试原理的关系,出现了明显的规律性,这在信息安全应用中是一个极大的安全缺陷。
(2)FIPS 140-2测试
FIPS 140-2是NIST[8]所发表针对密码模块的安全需求,它具体实现了4随机性统计测试方法,而且提供了统计量的计算值必须满足的精确界限。其测试序列长度固定为20 000比特位,若其中任何一个测试失败,则该序列便未通过FIPS 140-2统计性测试。表1、表2是1 000次测试中FIPS140-2测试的通过次数。

表1 μ0=4.0时量化算法的测试通过次数

表2 μ0=3.98194327时量化算法的测试通过次数
从上述测试结果可以看到,粗粒化量化的效果比较差,这与谱测试结果类似。而对于二值量化,μ0=4.0时量化序列通过率明显好于μ0=3.981 943 27时量化后的序列。随着变小,其通过率急剧下降接近于0,说明量化序列的随机性要依赖于混沌序列的随机性,对μ0极度敏感。上述测试结果与二维谱测试结果相吻合,再一次说明了这两种量化算法的缺陷,这在信息安全应用中应该引起极大的重视。
3 混沌量化算法的改善
3.1 改进建议
混沌系统由于其轨迹的复杂性以及对初值的高度敏感性,一般的量化都不能有效地保留其混沌特性,这是量化的难点。因此要利用混沌序列的先天特性,还必须使用外部手段和方法对混沌序列进行处理。针对传统量化函数的特点以及混沌安全系统的要求,在设计和改进混沌量化算法时应考虑以下问题:(1)稳定性,即量化函数的优劣不依赖于混沌系统所产生的混沌序列。(2)量化的非周期性,即周期性混沌轨道不应产生周期性的量化序列。(3)混沌轨道的映射关系应为多对多,而不是传统的多对一。(4)量化效率,即量化函数应该同时考虑整个系统的速度。
从上述对Logistic混沌系统的量化和测试结果可以看到,被大量文献所采用的二值量化方法和多次粗粒化方法都存在很大缺陷。因此使用Logistic混沌的安全系统应该注意:若使用二值量化来量化混沌系统,则系统参数μ0应该取固定值4,否则参数的变化会使得随机序列的性能急剧下降;另外尽量不要使用多次粗粒化方法,因为量化后序列相邻两点存在比较固定的关系,很容易遭到攻击。
3.2 算法的改进
下面提出一种等分区间的动态量化算法,即将(0,1)区间等分为 28=256份,每一个区间对应一个 8位的0~255内的二进制整数。传统算法是将每个等分区间一一对应一个整数,按大小顺序相对应,通过改进则可以使区间的对应模式动态改变,由密钥控制,即不同的密钥将决定不同的区间对应模式,而且在量化的过程中也可以对模式动态地进行修改,而不是一成不变。图2是传统量化与改进的动态量化原理对比图。
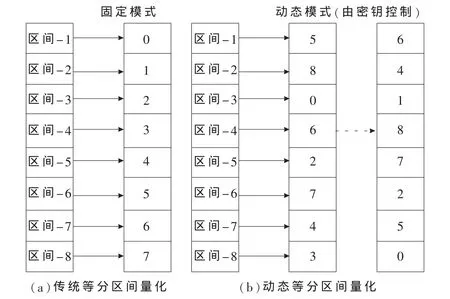
图2 传统量化与改进的动态量化原理对比图
如图2(b)所示,改进后算法由密钥来控制划分的模式,因此根据密钥的不同,量化的模式也不相同,形成一种实现简单、结果复杂而且效率很高的动态量化算法。图3为对该动态量化算法进行二维谱测试结果。
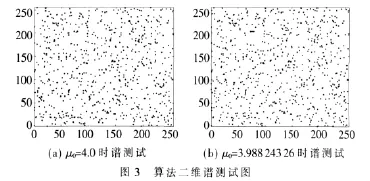
由图3可以看出,改进后的动态量化算法谱测试中点的分布有了明显改善,说明其随机性有了较大提高。表3是采用相同参数值对改进的算法进行FIPS140-2测试的数据,从结果对比来看,随机性明显好于传统算法。而且经过多次测试以及其他随机性测试也出现了同样的结果,这说明通过外部手段的作用,可以改变混沌伪随机序列的相关性能,从而可以合理利用μ0处于混沌范围内的其他值。同时也说明合理的选择动态模式会对随机性产生重要影响。

表3 改进的动态量化算法的FIPS140-2测试结果
本文从随机性角度对上述常见的两种量化算法进行了对比测试,并在此基础上进行了改进,其结果对于设计安全的混沌加密算法具有一定的指导作用。本文的测试一方面采用多种测试手段和标准,测试次数和系统初值分布全面,测试结果可靠,同时也可推广到高维混沌系统。
[1]陈关荣,汪小帆.动力系统的混沌化——理论、方法与应用[M].上海:上海交通大学出版社,2006.
[2]高俊山.基于混沌理论的加密过程的研究[J].自动化技术 与 应 用 ,2001(6):13-16.
[3]ZHOU H,LING X T.Generating chaotic secure sequences with desired statistical properties and high secuirty[J].Bifurcation and Chaos, 1997,7(1):205-213.
[4]PING Li, ZHONG Li, Siegfried Fettinger, et al.Application of chaos-based pseudo-random-bit generators in internet-based online payments.Studies in Conputational Intelligence(SCI)37, 2007:667-685.
[5]陈果,廖晓峰.一种新的基于混沌映射到分组加密方法[J].计算机工程与应用,2005(24).
[6]李建华.现代密码技术[M].北京:机械工业出版社,2007.
[7]黄方军.基于数字化混沌理论的信息安全研究 [D].武汉:华中科技大学,2005.
[8]胡汉平,董占球.混沌流密码研究[J].计算机安全,2005(9).

