样本大小对非平衡数据分类的影响*

职为梅，范 明，叶阳东

(郑州大学 信息工程学院，河南 郑州 450052)

分类是数据挖掘中的重要任务之一，在商业、金融、电讯、DNA分析、科学研究等诸多领域具有广泛的应用。统计学、机器学习、神经网络等领域的研究者提出了很多分类方法[1]。分类稀有类是分类中的一个重要问题。这个问题可以描述为从一个分布极不平衡的数据集中标识出那些具有显著意义却很少发生的实例。分类稀有类在现实生活中的很多领域都有广泛的应用。例如，网络侵入检测、欺骗探测和偏差探测。在网络入侵中，一个计算机通过猜测一个密码或打开一个ftp数据连接进行远程攻击。虽然这种网络行为不常见，但识别并分析出这种行为对于网络安全很有必要。

普通分类问题中，各个类包含的数据分布比较平衡，稀有类分类问题中，数据的分布极不平衡。例如：将一批医疗数据分类为“癌症患者”和“非癌症患者”两个类，其中 “癌症患者”是小比例样本(假设占总样本的1%)，称其为目标类，“非癌症患者”为多数类样本，称为非目标类，从大量数据中正确识别“癌症患者”就是稀有类分类问题。由于在数据集中所占比率太小，使得稀有类分类问题比普通分类问题更具挑战性。

研究表明，解决稀有类分类问题的方法总体上可以分为：基于数据集的、算法的[2]，以及使用组合分类器方法，如 Bagging、Random Forest及 Rotation Forest等。

影响稀有类分类的因素有很多，本文针对其中的一个因素——样本大小进行研究。实验基于上述的若干组合分类器，在特定的类比率[3]下通过改变样本大小，观察样本大小对稀有类分类的影响。

1 影响稀有类分类的因素

通常认为影响稀有类分类的因素是不平衡的类分布(Imbalanced class distribution)，但是大量的研究和实验证明，数据的不平衡性只是影响稀有类分类的一个因素，还有一些重要的因素影响稀有类分布，如小样本规格(Small sample size)和分离性(Separability)[2]。下面简单讨论这些因素对稀有类分类的影响。

(1)不平衡的类分布：研究表明，类分布越是相对平衡的数据分类的性能越好。参考文献[4]探讨了训练集的类分布和判定树分类性能的关系，但是不能确定多大的类分布比率使得分类性能下降。研究表明，在有些应用中1：35时不能很好地建立分类器，而有的应用中1：10时就很难建立了。

(2)样本大小：给定特定的类分布比率(稀有类实例和普通类实例的比值)，样本大小在确定一个好的分类模型中起着非常重要的作用，要在有限的样本中发现稀有类内在的规律是不可能的。如对于一个特定的数据集，类分布比率为 1：20，其中稀有类实例为 5个，非稀有类实例为100个。改变该数据集的样本大小，使得稀有类实例为50个，非稀有类实例为1 000个。结果是类分布同样为1：20，但是前者没有后者提供的稀有类信息量大，稀有类分类的性能没有后者高。

(3)分离性：从普通类中区分出稀有类是稀有类分类的关键问题。假定每个类中存在高度可区分模式，则不需要很复杂的规则区分它们。但是如果在一些特征空间上不同类的模式有重叠就会极大降低被正确识别的稀有类实例数目。

根据以上分析可知，由于影响稀有类分类的因素多种多样，使得稀有类分类问题更加复杂，分类的性能降低。本文在其他因素相同的前提下研究样本大小对稀有类分类的影响。实验证明在类分布相同的情况下，样本越大稀有类分类的性能越好。

2 稀有类分类的评估标准

常用的分类算法的评估标准有：预测的准确率、速度、强壮性、可规模性及可解释性。通常使用分类器的总准确率来评价普通类的分类效果。而对于稀有类分类问题，由于关注的焦点不同，仅用准确率是不合适的。

由线性拟合可以得到Q(hkl)，然后对所有的峰取平均可以得到t/G.图5是铬的P-t/G图.从图中可以看出，t/G在超过19 GPa后变得平坦，表明此时铬由于屈服发生塑性形变，此时t/G的数值为0.005.

在稀有类分类问题中应更关注稀少目标类的正确分类率。在评价稀有类分类时，还应该采用其他的评价标准。

这里假设只考虑包含两个类的二元分类问题，设C类为目标类，即稀有类，NC为非目标类。根据分类器的预测类标号和实际类标号的分布情况存在如表1所示的混合矩阵(Confusion Matrix)。

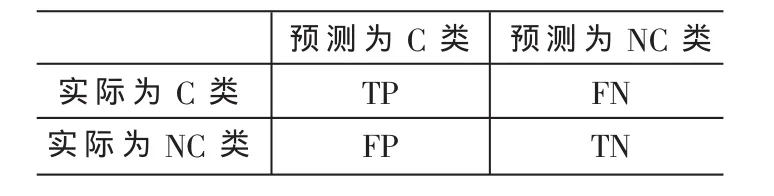
表1 二元分类问题的混合矩阵

根据表1得到如下度量：

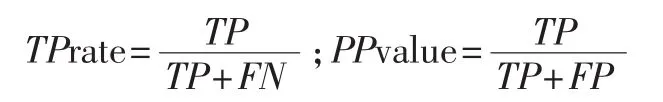
通常情况下使用召回率(recall)即 TPrate、精确率(precision)即PPvalue和F-度量来评估稀有类分类。F-度量(F-measure)由下式定义：F＝；其中R为recall，P 为 precision。

3 组合分类器介绍

组合分类器是目前机器学习和模式识别方面研究的热门领域之一，大量研究表明，在理论和实验中，组合方法比单个分类模型有明显的优势。组合方法由训练数据构建一组基分类器，通过对每个基分类器的预测进行投票后分类。常用的组合分类器有：Bagging、Random Forest及 Rotation Forest。

3.1 Bagging介绍

Bagging[5]算法是一种投票方法，各个分类器的训练集由原始训练集利用可重复取样 (bootstrap sampling)技术获得，训练集的规模通常与原始训练集相当。基本思想如下：给定s个样本的集合 S，其过程如下：对于迭代t(t=1，2，...，T)，训练集 St采用放回选样，由原始样本集S选取。由于使用放回选样，S的某些样本可能不在St中，而其他的可能出现多次。由每个训练集St学习，得到一个分类算法Ct。为对一个未知的样本X分类，每个分类算法Ct返回它的类预测，算作一票。Bagging的分类算法C*统计得票，并将得票最高的类赋予X[1]。

3.2 Random Forest介绍

随机森林是一种组合分类器方法，构成随机森林的基本分类器是决策树。基本思想如下：首先设定森林中有M棵树，即有M个决策树分类器，且全体训练数据的样本总数为N。使用bagging方法，即通过从全体训练样本中随机地有放回地抽取N个样本，形成单棵决策树的训练集。重复M次这样的抽样过程分别得到M棵决策树的学习样本。单棵决策树建造过程不进行剪枝，森林形成之后，对于一个新的样本，每棵树都得出相应的分类结论，最后由所有树通过简单多数投票决定分类结果。

3.3 Rotation Forest介绍

Rotation Forest是一个基于判定树的组合分类器，其基本思想如下：假设x=[x1，…，xn]为不含类标号的数据集X的一个元组，则该数据集可以表示为N×n的矩阵；定义Y=[y1，…，yN]为X中元组对应的类标号集合，其中 yi∈{w1，…，wc}；定义 D1，…，DL 为组合方法中的基分类器；F为属性集合。Rotation Forest意在建立L个不同的准确的分类器。特征集F被划分成K个子集，在每个子集上运用PCA[6](principal component analysis)进行特征提取，合并所有的主成份重建一个新的特征集，原始数据被映射到新的特征空间。基于新的数据集训练得到Di分类器。L次不同的属性集划分得到L个不同的提取特征集，映射原始数据得到L个不同的数据集，分别训练得到L个分类器。对于未知样本的实例X，组合L个分类器计算每个类的置信度，将其归类于置信度最高 的 类 中[6，7]。

4 实验结果及其分析

为了验证稀有类分类算法受到样本规格大小的影响，使用UCI机器学习库[8]中的稀有类数据集sick作为实验数据集。实验环境选择weka平台，使用weka平台提供的unsupervised resample数据预处理方法改变样本的大小。实验采用十折交叉验证的方法统计分类的准确率。

sick数据集的基本情况为：30个属性(带类标号)、2个类(0，1)，共有实例3 772条。其中 sick和negative类分别拥有实例数目3 541和231，分别占总样本比例93.88%和6.12%。sick类可看作稀有类。

4.1 实验结果

基于每个数据集，采用weka平台提供的unsupervised resample数据预处理方法改变样本规格的大小，使得实例数目分别是原始数据的倍到10倍不等。对这些处理后的数据集分别应用组合分类器bagging、FandomForest和Rotation Forest算法进行分类。

表2是应用Rotation Forest算法在处理后得到的sick数据集上关于sick类的实验结果。sick数据集样本被扩充了若干倍不等。

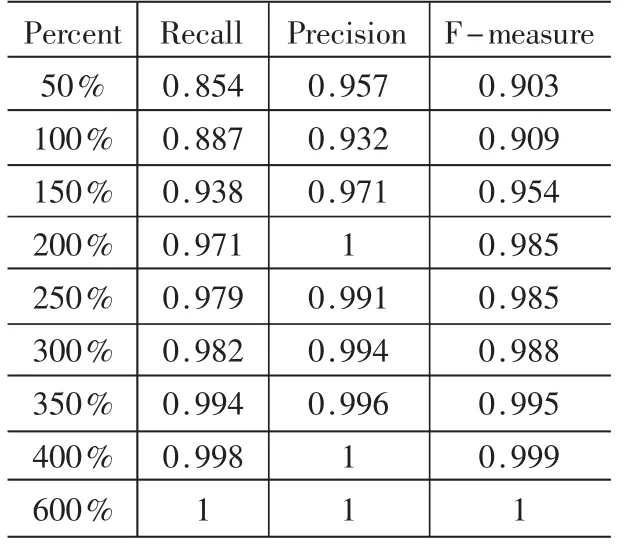
表2 Rotation Forest在sick上的实验结果

表3是应用Random Forest算法在处理后得到的sick数据集上关于sick类的实验结果。sick数据集样本被扩充了若干倍不等。

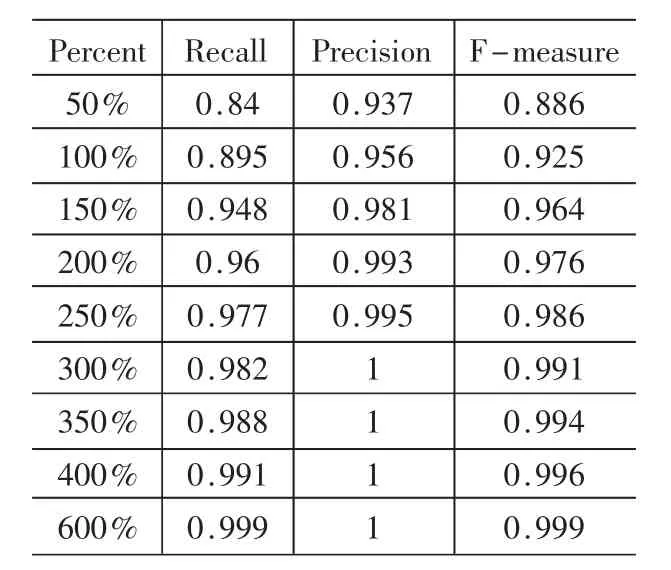
表3 Rotation Forest在sick上的实验结果

表4是应用Bagging算法在处理后得到的sick数据集上关于sick类的实验结果。sick数据集被扩充了若干倍不等。Bagging算法在sick数据集上实验时，样本被扩充到10倍后，recall值仍没有达到1，后来实验又将样本扩充至12倍，但由于内存不够实验终止。

通过上述表格中的实验结果，可以看到随着样本规格变大，衡量稀有类分类的这些参数也呈递增。这也意味着随着稀有类实例数目的增加，算法可以获得更多关于稀有类的信息，从而有利于对稀有类实例的识别。

4.2 结果分析

通常认为影响稀有类分类的重要因素是数据分布的不平衡性，也就是说对于稀有类问题，普通的分类算法往往失效，但本文的实验结果表明，数据分布的不平衡性影响稀有类分类的一个因素，在特定的类比率下，使样本规格变大，普通的分类算法往往也可以取得很好的分类结果。

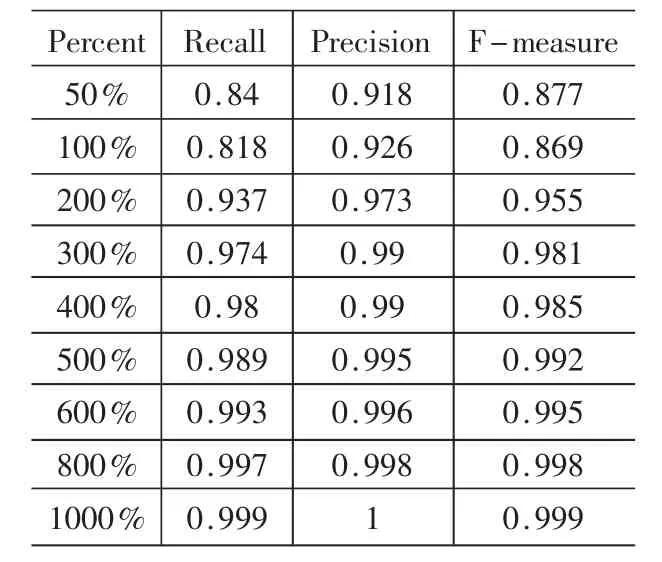
表4 Bagging算法在sick上的实验结果

本文对稀有类分类问题进行了研究，分析了影响稀有类分类问题的因素，探讨了稀有类分类的评估标准。针对影响稀有类分类的一个因素：样本规格的大小进行研究，在同等类分布比率下，改变样本规格的大小，在weka平台下进行实验，得到数据集中稀有类的recall、precision和F-measure值。实验结果表明，在特定的类比率下，使样本规格变大，普通的分类算法往往也可以取得很好的分类结果。同时也说明，数据分布的不平衡性只是影响稀有类分类的一个因素，即使数据分布极不平衡，通过增加样本中稀有类实例的数目(类比率不变)，也可以提高稀有类分类的各个指标。

本文中的实验基于多个组合分类器进行，每个组合分类器在每个数据集下的实验结果都表明了样本大小是影响稀有类分类正确的重要因素。在数据分布及不平衡下提供足够的稀有类实例仍然可以获得好的分类结果。

[1]HAN J，KANBER M，著，数据挖掘：概念与技术[M]，范明，孟小峰，译.北京：机械工业出版社，2001.

[2]Yanmin， Mobamed S.Kamel， Andrew K.C.Wong， Costsensitive boosting for classification of imbalanced data.Patter Recognition， 2007(10)：3358-3378.

[3]VISA S，RALESCU A.Issues in mining imbalanced data sets-a review paper[C].In Proceedings of the Sixteen Midwest Artificial Intelligence and Cognitive Science Conference， 2005：67-73.

[4]WEISS G，PROVOST F.Learning when training data are costly：the effect of class distribution on tree induction[C].J.Aritif.Intell.Res， 2003(19)：315-354.

[5]Breiman.Bagging predictiors[M].Machine Learning， 1996，24：123-140.

[6]KUNCHEVA L I，RODRIGUEZ J J， An experimental study on Rotation Forest ensembles[C].In：MCS 2007， Lecture Notes in Computer Science， vol.4472， Springer， Berlin，2007：459-468.

[7]RODRIGUEZ J J， KUNCHEVA L I， ALONSO C J.Rotation forest：a new classifierensemblemethod[C].IEEE Trans.Pattern Anal.Mach.Intell.2006，28：1619-1630.

[8]BLAKE C.MERZ C.UCIrepositoryofmachinelearning databases.http：//www.ics.uci.edu/～mlearn/MLRepository.html.1998.