B-值随机级数的强可积性
2010-11-26 04:27张颖周娟
湖北大学学报(自然科学版) 2010年4期
张颖,周娟
(湖北大学 数学与计算机科学学院,湖北 武汉 430062)
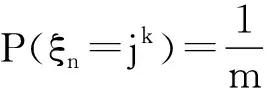
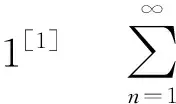
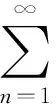
(1)
则
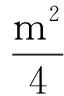
(2)
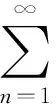
(3)
则
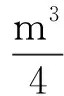
(4)
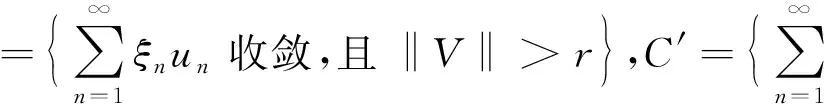
再定
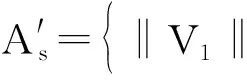
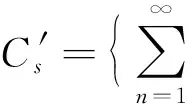
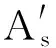

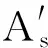
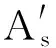
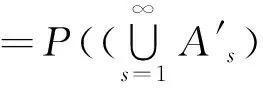
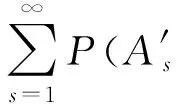
故
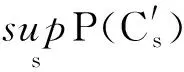
(5)
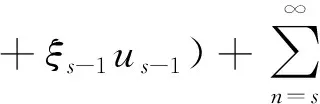
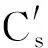
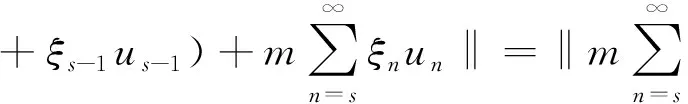
故V(1),V(2),…,V(m)中至少有一个向量在‖x‖≤r之外,相应有
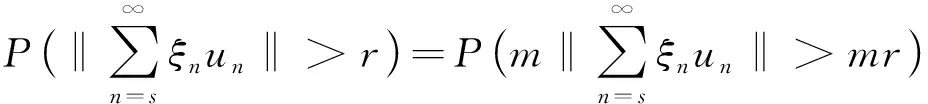
即
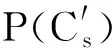
(6)
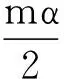
以同样的方法证明定理的第二部分,这里假设(3)式成立.
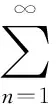
定理1的证明由Holder不等式只须证1≤p<∞成立即可.
设级数a.s.收敛,并考虑t≥0的一个连续递增函数φ(t),那么

(7)
其中P(t)=P(‖V‖>t).
又
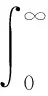
若
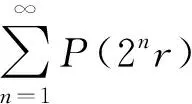
(8)
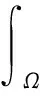
特别地,取φ(t)=tp,若从某项开始P(2nr)=0,则‖V‖p∈L1(Ω)显然成立.进而‖V‖属于所有的Lp(Ω)(0 这是由于 参考文献: [1] 杨薇娜.随机级数的a.s.S-可和性与a.s.收敛性[J].湖北大学学报:自然科学版,2006,28(1):7-8. [2] J-P卡昂纳.函数项随机级数[M].武汉:武汉大学出版社,1996:20-25.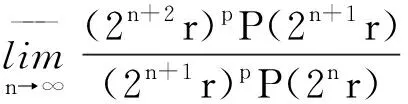




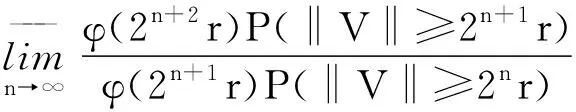
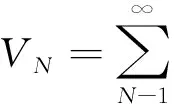
猜你喜欢
疯狂英语·新读写(2022年7期)2022-11-22
中等数学(2022年6期)2022-08-29
海峡姐妹(2020年2期)2020-03-03
校园英语·上旬(2019年6期)2019-10-09
学生天地(2019年30期)2019-08-25
数学年刊A辑(中文版)(2018年1期)2019-01-08
澳门月刊(2018年1期)2018-01-17
中学生数理化·七年级数学人教版(2017年6期)2017-11-09
山西大同大学学报(自然科学版)(2016年4期)2016-11-27
山西大同大学学报(自然科学版)(2016年6期)2016-01-30

