3-cactus上的连通p-median问题

陈光亭，辛 双，崔素辉

（杭州电子科技大学理学院运筹与控制研究所，浙江杭州310018）

0 引 言

p-median问题是选址理论中的经典问题，它是如下定义的：给定一个连通的无向图G=（V，E），V是顶点集合，E是边集合［1］。每一条边e∈E赋予一个非负的权重（长度）l（e），每一个顶点v∈V也有一个非负的权重 w（v）；d（vi，vj）表示vi和vj之间的距离，即连接vi、vj的最短路的长度。问题是找出一个含有p个顶点的子集H，使得v）d（v，H）最小。文献 1 证明了该问题是 NP-hard，文献 2 给出了一些近似方案。在树图上，文献1给出了一个O（p2n2）的算法，文献3给出了一个O（pn2）的算法 。在路图中，文献4给出了一个O（pn）的算法。在本文中研究这样的问题：选出的p个设施点是连通的，即由这p个顶点导出的子图是连通的，称为连通p-median问题。可以定义为：给定一个连通的赋权图G=（V，E），找出一个含有p个顶点的子集H，满足 G（H）连通，且v）d（v，H）最小［5］。由于树模型不能很好的表示现实的网络，而下面定义的cactus则能更好的反映现实的模型，因此本文研究cactus上连通p-median问题。

1 概念和符号

在一个图中，如果移去某个顶点及其关联的边，图的连通分支增加，那么该顶点叫做割点。一个没有割点的连通图称为不可分图；一个图中的极大的不可分子图称为块；圈是一个连通图，且每个顶点的度都是2。如果图中的块是个圈，那么称这个块为圈块。一个cactus是一个连通图，它的每一个块是三个或更多顶点的圈块。一个赋权的k-cactus（简记为WkC），它的每一个块至多包含k条边，每一条边和每个顶点都有一个非负的权重。如果k=3，则称为3-cactus。

应用广探法遍历一个图的顶点时，由于图顶点的有限性，广探法最终会停止；且图的每一个顶点恰被访问一次，因此遍历路径不会有圈形成。最终图的边可以分为两类：树边即广探法经过的边，和非树边即广探法未经过的边，非树边也称为桥边。

设G=（V，E，L，W）是一个赋权3-cactus图（简记为W3C），任选一个顶点r∈V作为图G的根，那么这个图就可以记为 G（r）。G（r）的距离块图 H（r）（简记为 W3B（r））是一个赋权图，是指将 G（r）中的每一个圈块转换成一个完全图 ，其它的结构保持不变 ；对H（r）中每一条边e=（u，v）∈H（E），令 lH（e）=dG（u，v），其中dG（u，v）表示u，v在G（r）最短路的长度。如果在赋权H（r）的底图上应用广探法，则访问路径可以得到一棵树，称为 H（r）的广探树，用 T（r）表示 H（r）的广探树。

对任一个赋权 3-cactus图 G=（V，E，L，W），任选一个顶点 r∈V作为根 ，记为 G（r），然后得到与G（r）相应的 H（r），对 H（r）应用广探法 ，得到相应的广探树 T（r）；在上述过程中 ，可以保持 G（r），H（r），T（r）中顶点的一致性，即在 T（r）中的顶点 v 与 G（r），H（r）中的顶点 v 代表同一个顶点。用 NT（u）表示H（r）中所有与u邻接的非树边的集合。对任意的u∈V（T），wT（u）=wH（u），lT（eu）=lH（u，v）=dG（u，v），eu=（u，v），v是u的父节点。对H（r）中的每一条非树边e=（u，v），令α（e）=lT（eu）+lT（ev））；其中WT（r）（u）=ANC（u）表示在 T（r）中 u 的前辈。

对 G（r）于中的顶点 ，可以分层标号 。令φ（r）=1，对任意的 v∈G（r），若（v，r）∈G（E），则φ（v）=φ（r）+1；对已标号的顶点 v，若（u，v）∈G（E），且 u 还没有标号，则φ（u）=φ（v）+1；对每一个顶点 v，定义son（v）=｛u|φ（u）=φ（v）+1，（u，v）∈G（E）｝，也称v是u的父节点，记为p（u）=v；若son（v）是空集，称v是叶顶点，否则为非叶顶点。对son（v）中的任意两个顶点u1，u2，若（u1，u2）∈G（E），则称u1，u2是兄弟 ，记 u1=b（u2）和 u2=b（u1），显然有φ（u1）= φ（u2）。对任意的顶点 u，用 G（u）表示由顶点集｛v|φ（v）≥φ（u）｝及删除边｛（u，x）|x=p（u）或 x=b（u）｝后所得到的子图。对 G（r）中的任意一对兄弟u，v ，用 G（u，v）表示由边（u，v）及 G（u）和 G（v）所组成的子图。对 G（r）的任一个连通 p-median M ，用δ（M）表示G（r）中所有顶点到M的赋权和。

引理1 设 M是G（r）的任意一个连通p-median，则下面两个结论中至少有一个成立：

（1）存在顶点 u，使得 M⊆G（u），且 u∈M；

（2）存在一对兄弟 u 和 v，使得 M⊆G（u，v），且 u，v∈M。

对任意的 G（u），用 Q（u）表示 G（u）上的任意一个最优连通 p-median（u∈Q）；对任意的 G（u，v），用Q（u，v）表示G（u，v）上的任意一个最优连通p-median（（u，v）∈Q）。显然有下面的引理成立：

引理 2 设Ω=｛Qu|u∈G（V）｝，Ψ=｛Q（u，v）|u，v是 G（r）中的兄弟｝。如果 Q∈Ω∪Ψ，且对任意的M∈Ω∪Ψ，都有δ（Q）≤δ（M），那么 Q是 G（r）的一个最优连通 p-median。

2 3-cactus上连通p-median问题的算法

用DT（u）表示T（r）中所有顶点到u的赋权距离和；B（u）表示T（r）的子树Tr（u）中的所有顶点到u的赋权距离和；B+（u）表示T（r）的子树Tr（u）中所有顶点到u的父节点P（u）的赋权距离和；Wr（u）表示T（r）的子树Tr（u）中所有顶点的权重和。

算法1

输入 一棵赋权树T（V，E）；

输出树T每个顶点的DT（u）。

第一步 任选一个顶点r∈V作为根，把输入的树T转化成一棵有根树，记这棵有根树为T（r）。

第二步对T（r）的每个顶点u∈V（T（r）），计算B（u），B+（u），Wr（u）；若v是T（r）的叶子，Wr（v）=w（v），B（v）=0，B+（v）=w（v）l（v，p（v））；若v不是T（r）的叶子，记son（v）=｛u|u∈V（T（r）），v是u的父节点｝，B（v）=u），B+（v）=B（v）+Wr（v）l（v，p（v））；B+（ r）=B（ r）。

第三步D（r）=B（r）；u∈V｛r｝，D（u）=D（p（u））-B+（u）+B（u）+（Wr（r）-Wr（u））l（（u，p（u）））。

算法2

输入 一个连通的赋权3-cactus。

输出 该图的连通p-median。

第一步 应用 Tarjan’s算法［6］，确定图 G（r）中的块。

第二步 得到相应的距离块图H（r）和对应于H（r）的广探树T（r）。

第三步对每一个顶点u∈G（r），在相应的广探树T（r）上计算R1（u）和R2（u）。

第四步对广探树T（r）中的每一个顶点u，应用算法1计算DT（u）。

第五步对H（r）中的每一个顶点u，计算DH（u）=DT（u）-R2（u）。

第六步对H（r）的每一条桥边e=uv，计算DT（e）；记它们的父亲为p（u）=p（v）=p（e）；DT（e）=DT（p（e））-（B（u）+B（v））+（BT（u）+BT（v））+（WT（r）-WT（u）-WT（v））min｛lT（u，p（e），lT（v，p（e））｝。

第七步DH（e）=DT（e），e是H（r）的桥边；Bh（u）=BT（u），u∈V（H）。

第八步对G（r）的每一个顶点v，计算RG（k-1，v，v），k≥1；对应于H（r）的每一条桥边e，计算RG（k-2，e，e），k≥2。

第九步从DH（v）-BH（v）+RG（p-1，v，v）和DH（e）-BH（e）+RG（p-1，e，e）（e=uv，BH（e）=BH（u）+BH（v））中找出最小的顶点 u 或边 uv，则 Q（u）或 Q（u，v）就是图 G 的连通 p-median；

给出计算RG（k-1，v，v）和RG（k-2，e，e）的递归算法：

若v是T（r）的叶子，则RG（k-1，v，v）=0，k≥1；

若u，v都是T（r）的叶子，且所对应的边是H（r）的桥边，则RG（k-1，（u，v），（u，v）=0，k≥2；

若uv是对应于H（r）的桥边，且u，v中至少有一个不是T（r）的叶子，则RG（k-2，uv，uv）=｛RG（i-1，u，u）+RG（k-i，v，v）｝，k≥2；若v不是T（r）的叶子，记son（v）=｛v1，v2，…，vs｝为v在T（r）中的子节点，判断 vi，vj是否为兄弟，若是，则

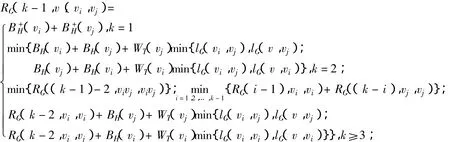
对vi，vj∈so（nv），且vi，vj是兄弟，用v*表示合并vi，vj后的记号，仍表示v的子节点，记（v*）=R（Gk-1，v，（vi，vj）），k=1；R（G（k-1）-1，v*，v*）=R（Gk-1，v，（vi，vj）），k=2；

R（G（k-1）-1，v*，v*）=R（Gk-1，v，（vi，vj）），k≥3；用so（nv）=｛v1，v2，…，vt｝（t≤s）表示合并v的子节点中是兄弟的所有子节点后的子节点集合，将原来G（r）中由vvi，vvj，vivj构成的圈，用vv*边来代替，这时G（r）也就转换成了一棵树。那么对于G（r）的每一个顶点，可以用下面的递归算法来计算所有的R（Gk-1，v，v），k≥1。

若 v 是 G（r）叶子，则 R（k-1，v，v）=0，k=1，2，…，p；否则，设 son（v）=｛v1，v2，…，vt｝，

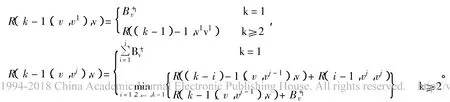
3 若干结论

结论1对任意的顶点v∈Gr（V），有DG（v）=DH（v）［7］。

结论2对任意的顶点v∈Gr（V），有BG（v）=BH（v）=BT（v），B+H（v）=（v）。

结论3若e=（u，v）∈Gr（E）是对应于H（r）的桥边，则有DG（u，v）=DH（u，v）=DT（u，v）。

4 算法复杂性分析

首先，在中T（r）计算DT（v），DT（e）（e是对应于H（r）的桥边）的复杂度为O（n）；其次计算G中每个顶点v的RG（p-1，v，v）的复杂度为O（d（v）p），其中d（v）表示v在G中的度；最后计算对应于H（r）的每个桥边e的RG（p-1，e，e）复杂度为O（p）。因此得到所有的RG（p-1，v，v）和RG（p-1，e，e）的复杂度为 O（pn）。应用 Tarjan’s［6］的算法，算法 2的第一步可以在 O（m+n）内完成；由图 W3C构造 W3B也是 O（m+n），其中m是图G中的边数，也是O（n）。因此整个算法的复杂度为O（pn）。

［1］ Kariv O，Hakimi SL.An algorithmic approach to network location problems.II：the p-medians［J］.JAppl Math，1979，37（3）：539-560.

［2］ Lin A JH，Vitter JS.Approximations with minimum packing constraint violation［M］.Brown University：Department of Computer Science，1992：29-92.

［3］ Tamir A.An O（pn2）algorithm for the p-median and related problems on tree graphs［J］.Operations Researc letters，1996，19（2）：59-64.

［4］ Hassin R，Tamir A.Improved complexity bounds for location problrms on the real line［J］.Oper Res Lett，1991，10（1）：395-402.

［5］ Chen Chien Tsai.The p-center problem with some practical constraints［J］.Department of Information Management，2006，52（1）：1-4.

［6］ Tarjan R E.Depth first search and linear graph algorithms［J］.SIAM journal on Computing，1972，2（1）：146-160.

［7］ Lan Y，Wang Y.An optimal algorithm for solving the 1-median problem on weighted 4-cactus graphs［J］.European joural of operational research，2000，22（1）：602-610.