关于加权的Bernstein-Markov型不等式

逯文鸣，赵 易

（杭州电子科技大学数学研究所，浙江杭州310018）

0 引 言

Bernstein算子是一类重要的线性算子，在逼近论及计算数学等方面有着许多应用。设C［0，1］表示在［0，1］上定义的连续函数全体，对任意的 f∈C［0，1］，Bernstein 算子有如下的定义：B（f，x）：=，k=0，1，…，n，关于Bernstein算子的研究结果非常丰富。其中，Bernstein-Markov型不等式是研究的问题之一。数学研究者们曾给出一系列的结论，比如在文献1中，有结论‖B′（f）‖［-1，1］≤n2·‖B（f）‖；而在文献2中，给出了‖φ2B″（f）‖［-1，1］≤Cn‖f‖［-1，1］。近年来，许多国外国内学者关注具有奇性的函数，DellaVecchia D，赵易等都对其进行了研究，参考文献3，4。通过多项式来研究带有奇点的函数的逼近及相关结论，无论在理论和应用方面都有重要意义。论文主要研究关于奇性函数的Bernstein-Markov型不等式，并把文献2的结果作了推广。

1 主要结论

要实现Bernstein多项式对此类函数的逼近，必须对其进行修正：对任意 f∈Cw，修正的Bernstein算子定义为：

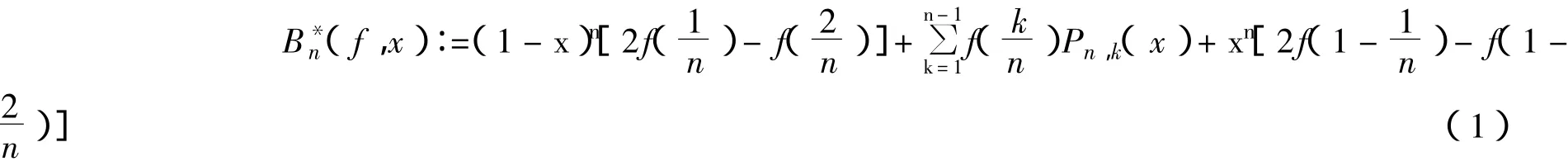
本文对上述不等式进行推广，有如下Bernstein算子关于奇性函数的Bernstein-Markov型不等式：

式中，分别令λ=0及λ=1，则有：

推论1

推论2

其中推论2即为文献2中结论，即不等式3，且此不等式从函数具有奇性的角度推广了文献2。

2 主要结果及证明

式中，Ih=［16h2，1-16h2］，

引理 1 对任意的α，β＞ 0，f∈Cw，有‖w（f）‖≤C‖wf‖。

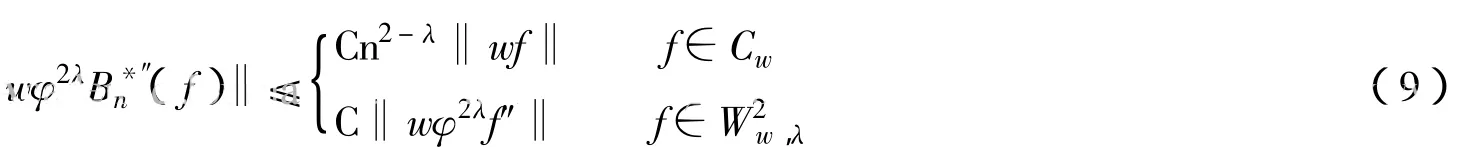
定理1 对任意的α，β＞0有：证明 （1）当 f∈Cw时，分两种情况讨论：1）当 x∈［0］时，我们有|w（x）φ2λ（x］时，类似可得

根据以上有：

容易算得A（0x）=n w（x）φ2λ-（2x）B*n（f，x）≤Cn2-λ‖wf‖ 。又有A（1x）=w（x）φ2λ-（4x）

［1］ Duffin R J，Scheaffer A C.A refinement of an inequality of the brothers mark off［J］.Trans Amer Math Soc，1941，（50）：517-528.

［2］ Della Vecchia，DMastroianni，G Szabados J.Weighted approximation of functions with endpoint or inner singularities by Bernstein operators［J］.Acta Math Hungar，2004，103（1-2）：19-41.

［3］ Ditzian Z，ToticV.Moduli of smoothness［M］.New York：Springer-Verlag，1987：112-157.

［4］ 郭顺生，陈伟英.Bernstein算子带权同时逼近的点态结果［J］.应用数学学报，2005，28（3）：466-481.

［5］ Wei Bao-rong，Zhao Yi.Weighted approximation of functions with singularities by Bernstein operators［J］.Zhejiang Univ Sci，2008，9（10）：1 451-1 456.