关联模式识别与预测在证券市场的应用

沈明宇

(武汉工程大学 智能机器人湖北省重点实验室，湖北 武汉 430073)

股价的预测长期以来都是人们所关注的焦点，传统的分析方法一般有两种：基本面分析法和技术分析法.但由于股价的变化情况一方面受供求、政治、经济、军事以及国际形势的影响，另一方面还受到其他一些复杂因素的影响(如：不完全信息和不确定性因素)，因此两种预测方法效果各有千秋，有时前者占上风，有时后者较准，总的来说效果并不十分理想.本文中一方面脉承文献[1]中所采用的混沌动力学方法，即将一维时间序列通过相空间扩维，变化为多维时间序列模式的分析思想，通过灰关联分析方法并结合其他金融理论找出最佳的维数，以此维数为基础将历史数据看成一个一个的“标准模式”，与现在的数据进行关联模式识别，以获得对未来的预测值；另一方面我们对灰关联分析方法进行改良.

1 股价时间序列扩维与灰关联分析

唯物辩证法告诉我们事物的发展是一种螺旋式的上升的过程，文献[1]基于混沌动力学和灰关联分析，提出了一种灰关联模式识别与预测方法，并将其应用于中长期径流预报中.我们对其进行了部分修改，并将其应用于股市短期预测中.其思路结合本文内容介绍如下.基于全信息观点即一个系统的输出(股指的变动)内含的信息最丰富，是系统输入(各种渠道的消息：这里的消息既包括政府公布的消息又包括人为炒作的假消息还包括通过各种途径得到的消息,但有一个前提是此消息必须是人们无法通过旧的信息推出的且尚未完全过时效的信息.)和系统本身(股市自身发展变化的规律)综合作用的结果，隐含着系统最本质的信源.但需要指出的是，过去股价分析仅习惯于一维时间序列分析，仅为信源的一个部分.本文中将吸取混沌动力学中相空间扩维思想，以获得股价变动更多的信息.因为股价序列从时间轴上看是一维的，如{x(k)} k=1,2,…,n,但按滑动生成的相空间看，则是多维信源，如：{x(k)}k,{x(k+1)}k,…,{x(k+l)}k.后者信息丰富得多.如果我们把扩维的每个序列视为一个个“模式”，则“过去”与“现在”，“现在”与“将来”的相似规律判别归为模式相似程度判别.从系统分析原理上讲，是多个数列的序化分析.将灰关联分析法应用到上述模式判别，便可进行未来相似模式的预测.这就是灰关联模式识别与预测的基本思想.其基本要点是一维时间序列的扩维和灰关联模式识别与预测.二者之间的联系有称之为灰周期的参数m(⊗)，这里⊗是灰变量特指符.不失一般性，记股价短期预测变量为x(t).它的离散样本集便构成一个一维序列x0，即： x0={x(1),x(2),…,x(n)}

(1)

(2)

其中Xp×m∈χ.

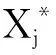
由于现有关联度多存在诸多不足，故本文中采用我们自创的关联度方法：三角关联度.

2 三角关联度

为使灰关联度模型能用于股市预测，我们构造了一种便于逆算的关联度—三角关联度，该关联度不仅沿用文献[2]的先定性分析，后定量计算的原则，将值域由[0,1]，扩展为[-1，1]，其具有文献[2]的一切优点，且计算公式简便，便于编程.

其具体计算步骤如下.

原始参考序列：X:{x(k),k=1,2,…,n},原始比较序列：Y:{y(k),k=1,2,…,n}.

(1)定性分析.类似于文献[2]已作的详细阐述，我们应先对所研究的序列作定性分析，然后根据具体情况选择初值化方法.

(2)一次累减生成序列.根据分析结果，若为第一种情况则：

ax(k+1)=x(k+1)-x(k),ay(k+1)=y(k+1)-y(k),k=1,2,…,n-1.

并将此过程称为绝对初值化方法.

若为第二种情况则：

并将其称为相对初值化方法，其实质是研究每单位基数的变化率.

(3)计算各段折线的关联系数

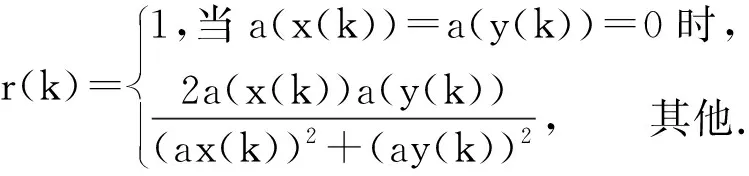
(4)计算三角关联度的值： r(X,Y)=(r(1)+r(2)+…+r(n-1))/(n-1).

3 对三角关联度性质的初步研究

我们建立平面直角坐标系，以a(x(k))为x轴上的坐标值，以a(y(k))为y轴上的坐标值(k=1,2,…,n-1),从坐标图形上观察a(x(k)),a(y(k))与r(k)的关系，从而得出一些基本性质.

图1 三角关联度的性质

从图1上我们不难发现

r(k) =2a(x(k))a(y(k))/(a(x(k))2+a(y(k))2)=

2sinA(k)cosA(k)=sin2A(k).

性质1 -1≤r(k)≤1,-1≤r≤1;

性质2 r(k)=1的充要条件是a(x(k))=a(y(k))(k=1,2,…,n-1);

性质3 r(k)=-1的充要条件是a(x(k))=-a(y(k)) (k=1,2,…,n-1);

性质4 归零性.r(k)=0的充要条件是a(x(k)),a(y(k))中有一个是0，而另一个不是.

定义1 a(X)=a(Y)当且仅当a(x(k))=a(y(k))(k=1,2,…,n-1)时;a(X)=-a(Y)当且仅当a(x(k))=-a(y(k))(k=1,2,…,n-1)时.

性质5 r=1的充要条件是a(X)=a(Y). r=-1的充要条件是a(X)=-a(Y).也就是说当且仅当每一段折线斜率相等(或互补)时,r才等于1(或-1).

如果X，Y定性分析为第一种情形，则有下列性质.

性质6 r=0的充分条件是X,Y中有一个是常数序列，另一个不是.逆则未必.

性质7 易证下列公式：(1)r(X,Y)=r(Y,X);(2)r(X+C1,Y+C2)=r(X,Y)(其中C1,C2为常数列).

另外，由于本文中采取了先定性，后计算的原则,因此此关联度值具有唯一性，不会产生序数效应，因而具有可比性；再由于扩展了其值域，具备了灵敏性，客观性，规范性，从而具备了刻划上的精确性.

具体计算步骤如下：

设X={x(k),k=1,2,…,n}为参考序列，Y={Yj(k),k=1,2,…,n}为被比较序列，j=1,2,…,m.

将全部的Rj(j=1,2,…,p-1)按从大到小排列，便获得灰关联分析的序关系.

4 关联模式识别的预测方法

由于股价变化的随机性较强，作中长期预测可能效果不太理想，故本文中只将这种方法用作短期预测.其方法归纳如下.

(1)收集历史数据，如每天的开盘价、收盘价、最高价、最低价等等.

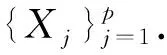
(3)取Xp={x(p),x(p+1),…,x(n)}为母序列，求出相空间各序列Xj(j=1,2,…,p-1)与Xp的关联度向量R和预报值向量，即

R={R1,R2,…,Rp-1},

Y={Y1,Y2,…,Yp-1}={x(m+1),x(m+2),…,x(n)}.

(4)由排序法确定关联度最大的相似模式序列Xp～Yj*，即

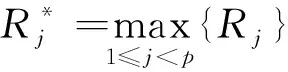
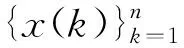
5 证券市场中的应用

本文中应用此方法采用1997年12月31日至1998年12月31日的上证综合指数对1999年的股市进行短期预测检验，预测结果见图2和表1：

表1 预测值与实际值的比较

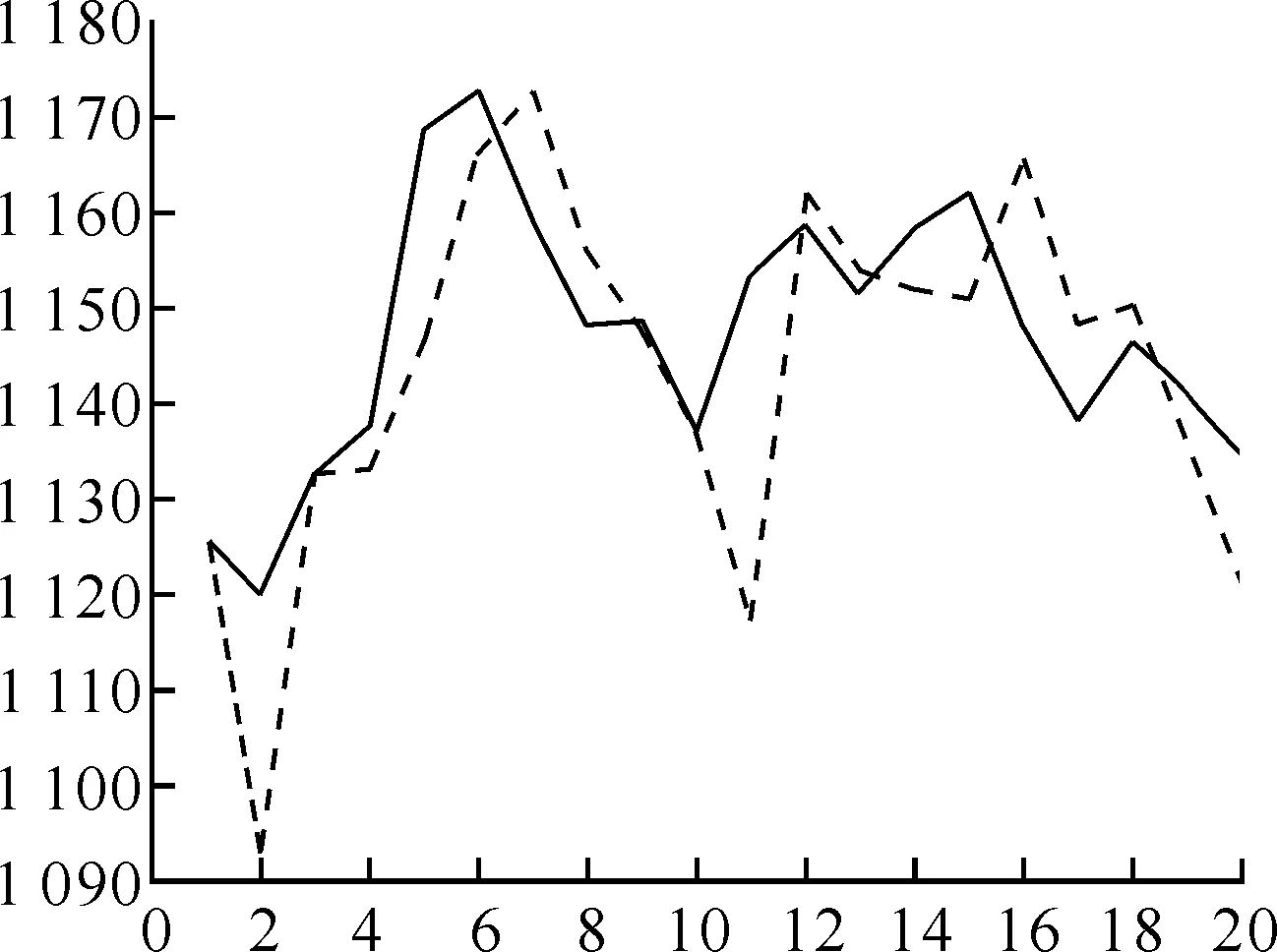
图2 预测值与实际值的比较

几点分析和说明如下.

(1)我们通过对上证综合指数股价序列进行相空间扩维，建立股指短期预测模式.

(2)对于维数的确定，我们是通过对1998年这一年的指数进行了不同维的关联分析，并结合江恩(W.D.Gann)理论中的重要的循环数将维数定为5日(即一周).实际上我们从经验上就知道股票的涨或跌持续的时间往往以周来计算.

(3)本文中采用的关联模型为我们自创的三角关联度模型，其优点前面已经阐述，在实际应用时也可根据实际需要采用其他模型进行预测.

(4)本文中方法预测效果较好，预测误差小于1%的达到70%，有一定的实际应用价值.

由于我们收集的数据较少，如果将所有历史数据收集起来，再根据这些历史数据进行不同维的关联分析确定更好的维数模式，预测效果会更好.

参考文献：

[1] 夏军.中长期径流预报的一种灰关联模式识别与预测方法[J].水科学进展,1993(3):190-197.

[2] 沈明宇,胡宝清.修正T型关联度及其在证券市场中的应用[J].系统工程理论与实践,2003(5):36-40.