2010年全国初中数学联赛模拟卷

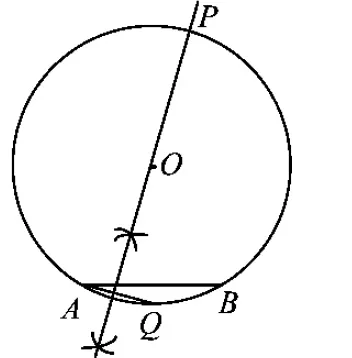
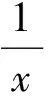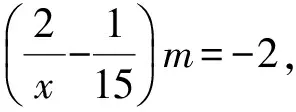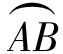2010年全国初中数学联赛模拟卷

1．已知：在△ABC中，∠ACB=90°，∠ABC=15°，AC=1，则BC的长为

( )

( )

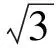
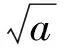
A.二者均为有理数 B.二者均为无理数

C.一个为无理数，另一个为有理数 D.以上3种情况均有可能

3．已知动点P在边长为2的正方形ABCD的边上沿着A-B-C-D运动，x表示点P由点A出发所经过的路程，y表示△APD的面积，则y和x的函数关系的图像大致为

( )

A. B. C. D.

4．已知二次函数y=ax2+c,且当x=1时，-4≤y≤-1，当x=2时,-1≤y≤5，则当x=3时，y的取值范围是

( )

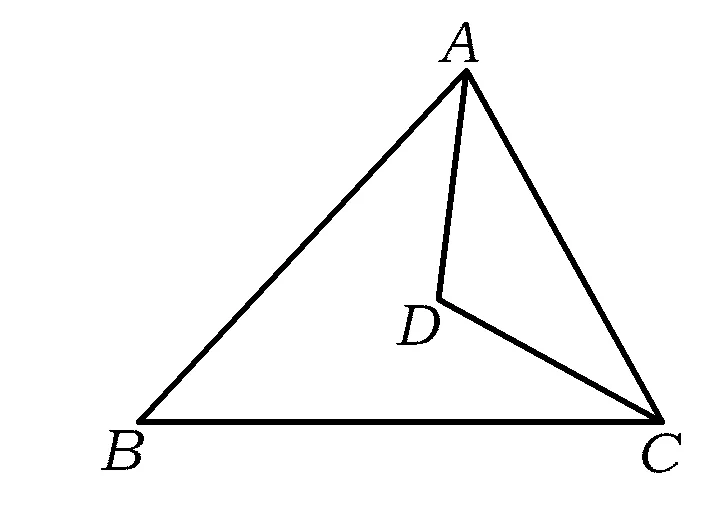
图1

5．如图1，已知在△ABC中，AB=AC，∠BAC和∠ACB的平分线相交于点D，∠ADC=130°，则∠CAB的大小是

( )

A.80°B.50°C.40°D.20°

6.若x0是一元二次方程ax2+bx+c=0(a≠0)的2个根，则判别式Δ=b2-4ac与平方式M=(2ax0+b)2的大小关系是

( )

A．Δ>MB.Δ=MC.Δ

二、填空题

7．将一个四边形的纸片一刀剪去一个角后，所得的多边形的内角之和是________.

8．观察下列各组数：(3，4，5)，(5，12，13)，(7，24，25)，(11，60，61)…，发现4=(32-1)÷2,12=(52-1)÷2,24=(72-1)÷2….若设某组数第一个数为k，则这个组的数为(k,________,________).

图2

图3

9．如图2是一个树形图的生长过程，依据图中所示的生长规律，第15行的实心圆点的个数等于________.

10．如果表示正方形ABCD各边长的代数式如图3所示，那么阴影部分的面积是________.

11.A,B,C,D,E,F这6个足球队进行单循环赛，当比赛进行到某一天时，统计出A,B,C,D,E这6个队已分别比赛了5，4，3，2，1场球，由此可知，还没有与B队比赛的球队是________

12.△ABC内接于⊙O，D是边BC上的中点，若∠ABC+∠DAC=90°，则△ABC是________三角形.

三、解答题

13．某同学买某种铅笔，当他买了x支，付了y元(x，y都是整数)时，营业员说：“你要再多买10支，我就总共收你2元钱，这样相当于每买30支，你可节省2元钱”,求x,y.

15．已知：关于x的方程①x2-(m+2)x+m-2=0有2个符号不同的实数根x1，x2，且x1>|x2|>0；关于x的方程②mx2+(n-2)x+m2-3=0有2个有理数根且两根之积等于2.求整数n的值.

16.讨论一道开放性试题，教师要求同组每个同学至少要和3个同学交换意见．某学习小组共有11位同学，讨论完成后有2位同学说自己和4个同学交换了意见．证明:至少还有1位同学也至少和4个同学交换了意见．

参考答案

13.解根据题意得，y的值只能是1或2.

此时m只能取15,30,45,60….经讨论后,只有当m=15，x=5时,才符合题意.

(2)当y=2时，

无论m为何整数均不合题意.故x=5,y=1.

图4

图5

(2)能取得最大值,如图5所示.

15.解由方程①及x1·x2<0，x1>|x2|>0,知x1>0,x2<0.由

Δ=(m-2)2+8>0,

得

x1+x2=m+2>0,x1·x2=m-2<0,

从而

-2

由方程②知

即

m2-2m-3=0,

解得

m=3(舍去)，m=-1,

代入方程②得

x2-(n-2)x+2=0.

因为方程的2个根为有理数，所以

Δ=(n-2)2-8=k2,

即

(n-2)2-k2=8,

得

(n-2+k)(n-2-k)=8,

从而

解得

n=5或n=-1.

16.证明因为甲、乙2人相互讨论1次，每人都说自己讨论了1次，在统计时，就被算作了2次.

在11个人中，若每人刚好只讨论了3次，则总次数将是11×3=33次，

由于其中有2个人是讨论的4次，因此总次数是33+2=35次．

根据前面的分析可知，对每一次讨论都有2个人报数，故总次数应该是2的倍数，故总次数>35．即总次数至少是36次，因此一定至少还有1个人是讨论的4次．

(浙江奥数网提供)