二维Landau-Lifshitz-Darwin耦合模型整体弱解的存在性
黄丙远, 丁时进
(华南师范大学数学科学学院,广东广州 510631)
二维Landau-Lifshitz-Darwin耦合模型整体弱解的存在性
黄丙远, 丁时进*
(华南师范大学数学科学学院,广东广州 510631)
运用先验估计和Galerkin方法,证明了二维Landau-Lifshitz方程耦合Maxwell方程的Darwin模型的整体弱解存在性.
整体弱解; Landau-Lifshitz方程; Darwin模型; Galerkin方法
本文考虑二维Landau-Lifshitz方程耦合Maxwell方程的Darwin模型
ut=u(Δu+HD)-u(u(Δu+HD)),
(1)
-Δ(HD+u)=×f+××u,
(2)
(3)
(4)
(5)

关于Maxwell 方程耦合Landau-Lifshitz 方程,已经有了很多工作.例如, GUO和SU[1]利用Galerkin方法建立了在三维空间中周期初值的整体弱解存在性,DING等人[2]利用Galerkin 方法及粘性消失逼近获得了Landau-Lifshitz-Maxwell方程的整体弱解存在性, CARBOU和FABRIE[3]利用Ginzburg-Landau逼近方法证明了在三维空间中Neumann 边值的整体弱解存在性,并且通过时间平均方法研究了弱解的长时间性态.
但是, 当没有高频现象或电流变化不快时,Darwin模型是Maxwell方程组的一个很好的逼近模型,已在文献[4]-[6]中研究过. Landau-Lifshitz方程耦合Darwin模型的局部正则解在文献[7]中已研究,本文考虑它在二维空间中整体弱解的存在性.
本文考虑的Landau-Lifshitz-Darwin模型是包含着Landau-Lifshitz方程与Darwin模型. 对于方程(5),容易得到它的解,我们只需要研究方程(1)~(4),证明它的周期边值的整体弱解存在性.
我们称函数f(x)为2D-周期函数, 如果f(x+
2Dei)=f(x) (i=1,2), 其中(e1,e2)为2的单位正交基,常数D>0.
这里对方程(1)~(4)提出下面初值条件

(6)
本文假设u0(x)是2D-周期. 我们记Ω⊂2 为二维空间中每个方向的宽度都是2D的, 也就是,Ω={x=(x1,x2)xixΩ, 0 注1 有关方程(2)~(4)的推导如下: (7) (8) (9) (10) 引理2[10]设ξ(t)在[0,T]上对几乎处处的时间t是非负可积函数,对于常数C1,C2≥0有积分不等式 成立. 那么,对于几乎处处的时间0≤t≤T,成立不等式 ξ(t)≤C2(1+C1eC1t). 引理3[11]设Banach空间X⊂E⊂Y且满足X''E. 那么下面的嵌入是紧的, 如果1≤q≤∞,或1 本部分我们将利用Galerkin方法获得问题(1)~(4)及(6)的整体弱解存在性. 设ωn(x) (n=1,2,3,…)为问题-Δωn=nωn,ωn(x-Dei)=ωn(x+Dei)的特征函数,且n(n=1,2,3,…)为相应的不同的特征值. 我们构造方程(1)~(4)及(6)的Galerkin近似解 (11) (12) (13) (14) 初值条件 (15) 显然成立 (16) 方程(11)写成以下形式 也就是 (17) 方程(12)写成以下形式 (18) 类似地, 方程(13)写成以下形式, 有 (19) 联合方程(17)和方程(18),我们得到关于αsN(t) (s=1,2,…,N)的非线性常微分方程 (20) 初值条件 (21) 问题(20)~(21)可归结为下面的一阶常微分方程 根据常微分方程组的基本理论, 方程组(11)~(16)存在唯一局部解. 由下面的先验估计,令N→∞,我们得到方程组(11)~(16)的整体解. (22) (23) 其中常数C,C1,C2,C3,C4不依赖于N. 方程(12)对时间t求导,得 (24) 把方程(3)变为 所以式(23)成立,其中C3=C2C2,C4=C2+C. 引理5 在引理4的条件下,对于初边值问题(11)~(16)的解, 有以下结果: (25) (26) (27) 其中常数C5,C6,C7,C8不依赖于N,2≤p<∞,q<2. 证明(1)用αsN(t)与方程(11)做向量积,并对s=1,2,…,N求和,得 那么成立 (28) (29) 用βsN(t)与式(11)做向量积, 并对积分求和,得 εuN (30) 应用引理1、引理4与式(28),得 (31) (32) 其中 用βsN(t)与式(12)相乘,对s=1,2,…,N求和再应用Cauchy不等式, 得 令ε=1/4,那么 (33) 联合式(32)与(33),有 C13+C14uN, (34) 其中 联合式(28)、(33)及(34),应用Gronwall不等式, 我们可得到式(25)、(27).利用嵌入定理及Hölder不等式,式(26)成立. 证毕. 引理6 在引理4的条件下,对于初边值问题(11)~(16)的解存在不依赖于N的C15>0,使得 (35) 其中p≥2. (36) 当s≥N+1, 成立 那么利用引理5,成立 证毕. 在引理6中取p=6,再应用引理4,有下面推论: 推论1 在引理4的条件下,对于初边值问题(11)~(16)的解存在不依赖于N的C16,C17>0,使得 (37) 首先, 类似于定义, 我们也可以定义问题(1)~(4)的弱解. 现在我们来证明下面定理. (38) (39) (40) (41) ∀p≥2; (42) (43) (44) (45) (46) 由式(41)与式(45)及引理3,有 uN(x,t)→u(x,t) inLp(QT), ∀p≥2. (47) 类似式(47)的证明,用式(43)、(46)及引理3,得 (48) (49) 用ηs(t)分别与式(11)~(13)做向量积,并对s=1,2,…,N的积分求和, 然后分部积分,得 (50) (51) (52) 利用引理4~引理6, 当N→+∞时,成立 (Ⅰ) 事实上 (Ⅱ) (Ⅱ)的证明和(Ⅰ)的证明类似,故此略去. (Ⅲ) 事实上 为了处理式(50)的最后一项,我们需要证明下面式子成立. (1)uNi=1,2; (53) (54) (asN→+∞), 其中已经用到式(41)、(47). 因此式(53)得证. 现在需要证明式(54). 由引理5知,(uN在L2(QT)中关于N一致有界, 那么(uN存在一个序列仍然记为(uN与一向量U(x,t)L2(QT), 使得对任意试验函数Ψ(x,t)C1(QT), 当N→+∞时,有 另一方面, 当N→+∞时, 其中已用到式(53). 事实上,当N→∞时, (55) 那么有 因此在分布意义下下式成立: uΔu=(U-(uH))L2(QT). 所以式(54)得证. 我们只需要证明 事实上, IN+JN+KN+LN. 由式(53), 当N→+∞时IN→0成立. 同时, 当N→+∞时, 成立 |JN|uN 类似地可得, 当N→+∞时,KN→ 0, [1] GUO B L, SU F Q. Global weak solutions for the Landau-Lifshitz-Maxwell equation in three space dimensions[J]. J Math Anal Appl, 1997,211: 326-346. [2] DING S J, GUO B L, Lin J Y, et al. Global existence of weak solutions for Landau-Lifshitz-Maxwell equations[J]. Disc Cont Dyna Syst, 2007,17(4): 867-890. [3] CARBOU G, FABRIE P. Time average in micromagnetism[J]. JDE, 1998,147: 383-409. [4] DEGOND P, RAVIART P A. An analysis of the Darwin model to Maxwell’s equation[J]. Forum Math, 1992,4: 13-44. [5] LIAO C X, YING L A. An analysis of the Darwin model of approximation to Maxwell equations in 3-D unbounded domains[J]. Comm Math Sci Commun, 2008,6(3): 695-710. [6] 廖才秀.达尔文模型的数值解及其应用[D].厦门:厦门大学,2008. [7] 陈美凤.Landau-Lifshitz方程耦合Darwin模型的解的存在性和唯一性[D]. 广州:华南师范大学, 2009. [8] JACKSON J D. Classical electrodynamics[M]. 3rd ed. New York:Wiley, 1999. [9] 陈亚浙. 二阶抛物型偏微分方程[M]. 北京: 北京大学出版社, 2003. [10] EVANS L C. Partial differential equations[M]. Rhode Island: Amer Math Soc Providence, 1998. [11] GUO B L, DING S J. Landau-Lifshitz equations[M]. Singapore: World Scientific, 2008. Keywords: global weak solution; Landau-Lifshitz equations; Darwin model; Galerkin method 【责任编辑 庄晓琼】 GLOBALEXISTENCEOFWEAKSOLUTIONSFOR2DLANDAU-LIFSHITZEQUATIONSCOUPLEDWITHDARWINMODEL HUANG Bingyuan, DING Shijin (School of Mathematics, South China Normal University, Guangzhou 510631, China) By using a priori estimate and the Galerkin method, the existence of the global weak solution for the two dimensional Landau-Lifshitz equation coupled with Darwin model of Maxwell equation is obtained. 2009-10-30 国家自然科学基金资助项目(10471045);广东省自然科学基金资助项目(7005795);国家973项目(2006CB805902) 黄丙远(1983—),男,广东湛江人,华南师范大学2007级硕士研究生,Email:huangby8@yahoo.cn;丁时进(1959—), 男, 湖南常德人, 博士, 华南师范大学教授,博士生导师,Email:dingsj@scnu.edu.cn. *通讯作者 1000-5463(2010)03-0024-07 O175.4 A



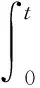


1 初边值问题的逼近解

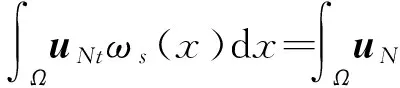

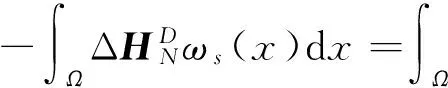

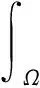
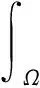
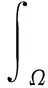
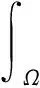
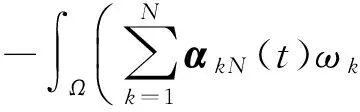
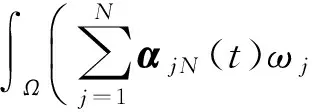
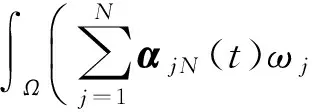
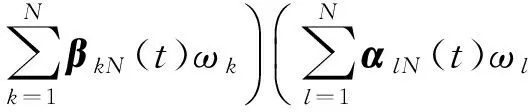
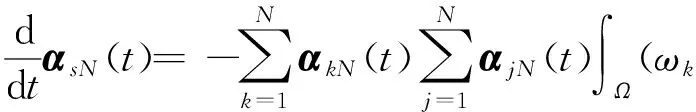
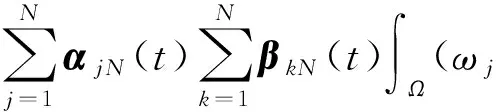
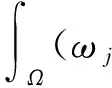

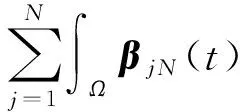
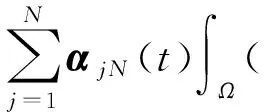

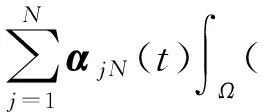
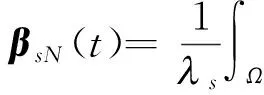
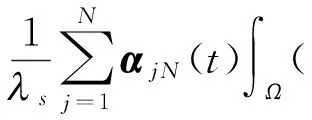
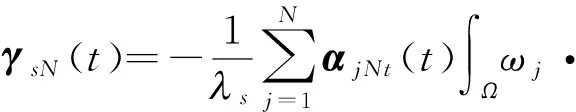
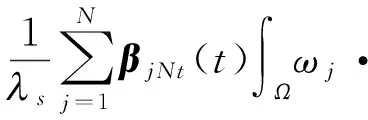
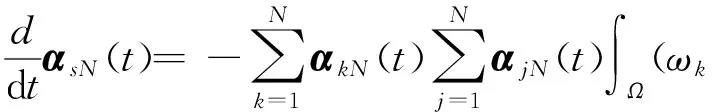
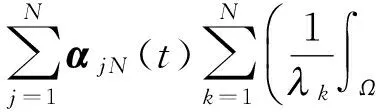
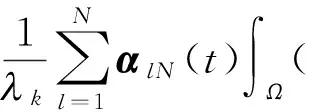
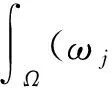



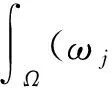
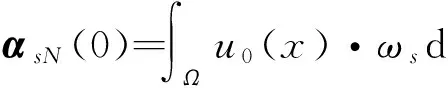
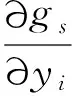


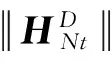


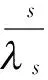
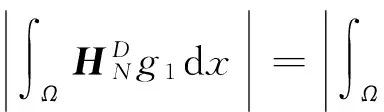
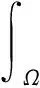
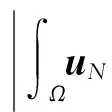
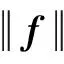
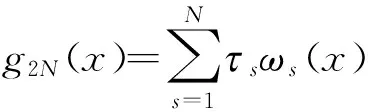
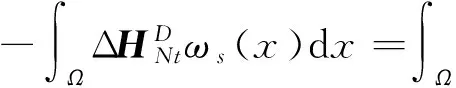
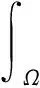
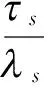
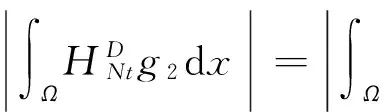

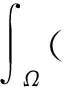
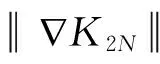
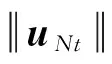
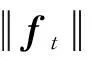

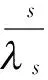
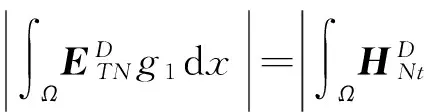
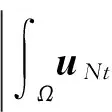
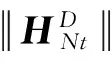
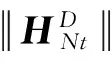
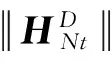
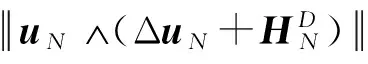
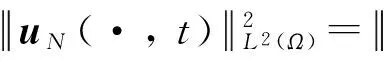

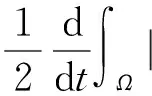
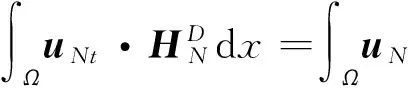
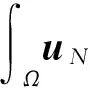
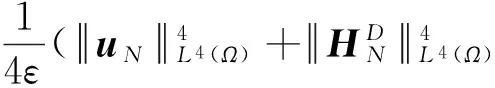

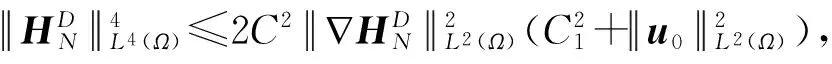
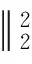
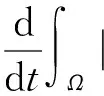
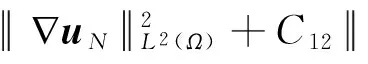
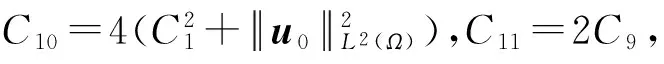
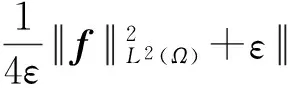
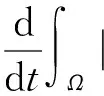

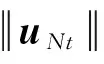

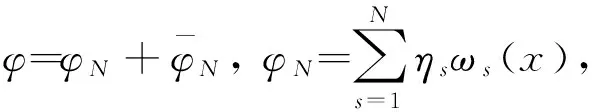
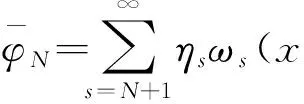
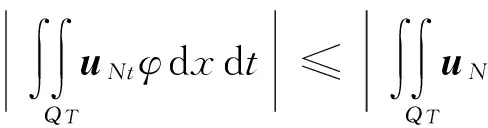
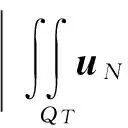
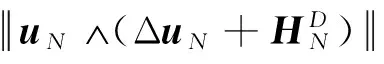
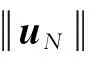
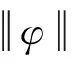
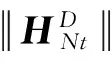
2 弱解的存在性