一类具有反馈控制Logistic模型周期解的存在性及全局吸引性
许钊泉, 翁佩萱
(华南师范大学数学科学学院, 广东广州 510631)
一类具有反馈控制Logistic模型周期解的存在性及全局吸引性
许钊泉, 翁佩萱
(华南师范大学数学科学学院, 广东广州 510631)
Logistic模型是种群生态学中一类描述种群动力学行为的最基本和重要的模型,而周期循环是自然界最常见的现象.基于对系统正平衡态位置及其稳定性进行控制的原理,提出一类具有周期系数和反馈控制的Logistic模型并对其动力学行为进行了研究,得到了正周期解的存在唯一和全局吸引的充分条件.
周期解; 全局吸引; 反馈控制; Logistic模型
随着社会保护环境、维护生态平衡意识的日益提高,如何有效管理和利用生物资源成为当今社会发展中颇为关注的问题.人们渴望通过各种手段使生物资源达到理想的平衡状态,达到维护生态平衡的目的. 数学生态模型中引进“反馈控制变量”作为一种外界手段可以通过捕获、改变物种生活环境等方式来实现,从而达到对物种的有效管理. 自GOPALSAMY和WENG在文献[1]中引入这个思想以来,许多学者对之很感兴趣,并致力于这类具有反馈控制变量的生态模型的研究,探索了这类系统的持久生存性、周期解的存在性及稳定性等问题[2-6]. 文献[1]研究了具有反馈控制变量模型:


(1)
给出了平衡点全局稳定的充分条件. 然而,我们知道自然界中有着很多周期因素,比如四季气候更替及生育规律等都会对物种有着很大影响. 基于这一考虑,我们研究具有周期系数的反馈控制系统:


其中ω>0,a(t),b(t),a1(t),a2(t),r(t),k(t),c(t)均为定义于+=[0,+∞)上的非负ω周期连续函数. 对于系统(2),我们考虑初值问题:


(3)

(4)

(5)
1 主要结果与证明
下面的4个引理描述了系统(2)的一些基本性质.
引理1 满足初值条件(3)的系统(2)的所有解在[0,+∞)上存在且恒为正.


由上式易见x(t1)>0, 这是矛盾的, 所以x(t)在[0,T)上恒为正的.从而由系统(2)的第2个方程有

由微分不等式的比较定理可得


而由系统(2)的第1个方程有
这是矛盾的, 这也就表明有限时间内x(t)不会趋向无穷大.同理可证有限时间内u(t)也不会趋向无穷大, 从而T=+∞,即满足初值条件(3)的系统(2)的所有解在[0,+∞)上存在且恒为正的.
引理2 满足初值条件(3)的系统(2)的所有解均有界,即对于满足初值条件(3)的系统(2)的任一解(x(t),u(t)),存在N*>0,M*>0, 使得 0 证明由引理 1可知满足初值条件(3)的系统(2)的解在[0,+∞)上存在且恒为正的, 假设满足初值条件(3)的系统(2)存在某个无界解x(t), 则存在序列tn,tn→∞(n→∞), 使得 (6) 然而对于足够大的n, 有 (7) 这与式(6)矛盾, 所以假设不成立, 从而存在N*>0,使得0 n≤x(t) ≤N,m≤u(t)≤M,t≥0, (8) 证明由系统(2)的第1个方程有 (9) 并注意到系统(2)的解恒为正的, 所以若0<φ(0)=x(0)≤N,由式(9)易见x(t)≤N对t≥0, 从而由系统(2)的第2个方程可得 (10) 由式(10)易见若0<φ(0)=u(0)≤M, 便有u(t)≤M对t≥0. 由上述结果及系统(2)的第1个方程有 (11) 若n≤φ(0)=x(0), 由式(11)易见n≤x(t)对t≥0,从而由系统(2)的第2个方程可得 (12) 若m≤φ(0)=u(0), 由式(12)易见m≤u(t)对t≥0. 引理4 若 (13) 则系统(2)满足式(8)的任何正解都是一致稳定的. 证明设Z1(t)=(x1(t),u1(t)),Z2(t)=(x2(t),u2(t))是系统(2)满足式(8)的任何2个正解, 则n≤xi(t)≤N,m≤ui(t)≤M(t≥0;i=1,2).定义一个李雅普诺夫函数V(t)=V(Z1(t),Z2(t))如下: (14) 沿着系统(2)的解计算V(t)的右导数得 (15) V(t)≤V(0). (16) 由中值定理易见 (17) 由式(14)、(17)有 (18) (19) 从而当 便有 定义1[7-8]向量函数P=(p1,…,pn):→n称为概周期的,如果对任意ε>0, 存在l=l(ε),使得对于任何长度为l的区间(a,a+l(ε)), 存在β使得ε.向量函数P=(p1,…,pn):→n称为渐近概周期的,如果它可表为一个连续概周期向量函数和一个当t→∞趋于零的连续向量函数之和, 即P(t)=F(t)+G(t), 其中F(t)为连续概周期向量函数 引理5[9]系统(2)的每一个有界且一致稳定的解是一个渐近概周期函数. 定理1 若引理3和引理4的条件满足,则系统(2)存在一个周期为ω的正周期解. 证明设N(t)=(x(t),u(t))为系统(2)满足引理3和引理4的假设条件的任一个解, 则由引理5,存在概周期函数N*(t)=(x*(t),u*(t))使得 x(t)=x*(t)+p(t),u(t)=u*(t)+q(t),t≥-ω, f(t,x*(t),u*(t))=r(t)x*(t)× 由文献[8]的定理2.7知f(t,x*(t),u*(t))是概周期的,又因为N(t)=(x(t),u(t))为系统(2)的解, 所以 f(t,x*(t),u*(t)),t≥0. (20) 显然当t→+∞时, f(t,x(t),u(t))-f(t,x*(t),u*(t))→ 0, (21) (22) 因此V(t)=V(N*(t),N*(t+ω))关于t非增且有界,从而 并且由式(21)有 (23) u*(s+ω)]ds≤V(0), 这表明 L1(0,∞). 是一致连续的.由Barbalat引理[11]有 定理2 若定理1的条件成立, 则系统(2)的正周期解N*(t)是全局吸引的. 证明设R(t)=(x(t),u(t))为满足初值条件(3)的系统(2)的任意解, 分别用R(t)和N*(t) 代替式(14)中的Z1(t)和Z2(t),仿照式(15)的推导易得 从而 (24) 这表明 是一致连续的.由Barbalat引理[11]有 运用本文类似的方法,我们不难证明周期系统: (25) 存在全局吸引正周期解的充分条件是 (26) 易见, 当r(t)=r,a1(t)=a1,a2(t)=a2,k(t)=k时,式(26)即为a1>a2. 作为系统(25)的特殊情形,文献[12]给出了系统: (27) (28) 此时bu=0,式(5)、(13)变为 (29) 由式(29)的第3个式子可知系统(28)的第2个方程仅有全局吸引的周期解u(t)=0, 从而可知此时控制变量u(t-ω)对系统(28)的第1个方程几乎没有什么影响,并注意到式(29)的第1个和第2个式子与式(26)相同,这也就表明控制变量u(t-ω)没有影响到系统(25)周期解存在性. 作为定理1和定理2的应用, 我们考虑系统(2)具有周期ω=π的系数: 则有: [1] GOPALSAMY K, WENG Peixuan. Feedback regulation of logistic growth[J]. Internat J Math Math Sci, 1993, 16: 177-192. [2] CHEN Fengde, SHI Jinlin. Periodicity in a Logistic system with several delays[J]. Computer and Mathematics with Applications,2004, 48(1-2): 35-44. [3] CHEN Fengde, YANG Jinghui, CHEN Lijuan. Note on the persistent property of a feedback control system with delays[J].Nonlinear Analysis: Real World Applications, 2010, 11: 1061-1066. [4] WENG Peixuan. Global attractivity in a periodic competition system with feedback controls[J]. Acta mathematics Applicatae Sinica, 1996, 12: 11-21. [5] LI Yongkun, Zhu Lifei. Existence of positive periodic solutions for difference equations with feedback control[J]. Applied Mathematics Letters, 2005, 18:61-67. [6] LI Yongkun. Positive periodic solutions for a periodic neutral differential equation with feedback control[J]. Nonlinear Analysis, Real World Application, 2005, 6:145-154. [7] AIZERMAN M A, GANTMACHER F R. Absolute stability of regulator systems (Translated from Russian)[M]. San Francisco:Holden Day, 1964. [8] YOSHIZAWA T. Stability theory and the existence of periodic solution and almost periodic solution[M]. Applied Mathematical Science, Vol.14, New York: Spring-Verlag, 1975. [9] HALANAY A. Differential equations; stability oscillations,Time Lags[M]. New York: Academic Press, 1966. [10] CORDUNEANU C. Almost periodic functions[M]. New York:Inter Science, 1989. [11] CORDUNEANU C. Integral equations and stability of systems[M]. New York: Academic Press, 1973. [12] LENHART S M, TRAVIS C C. Global stability of a biological model with time delay[J]. Proc Amer Math Soc, 1986, 96: 75-78. Keywords: Logistic model;positive periodic solution; global attractivity; feedback control 【责任编辑 庄晓琼】 EXISTENCEANDGLOBALATTRACTIVITYOFPERIODICSOLUTIONOFALOGISTICMODELWITHFEEDBACKCONTROL XU Zhaoquan, WENG Peixuan (School of Mathematics, South China Normal University, Guangzhou 510631, China) Logistic equation is one of the most important model describing the dynamics of species population,and periodic phenomena are very popular in the nature. Based on the consideration of the control of the position of positive equilibrium and its stability, a Logistic model with periodic coefficients and feedback control is proposed in the present article. Sufficient conditions are derived for the existence, uniqueness and global attractivity of positive periodic solution for the proposed model. 2010-01-14 国家自然科学基金资助项目(10571064);教育部高等学校博士学科点专项科研基金资助项目(20094407110001) 许钊泉 (1984—), 男,广西贵港人, 华南师范大学2008级硕士研究生,Email:xiaozhao20042008@163.com; 翁佩萱(1951—), 女, 广东潮州人,博士, 华南师范大学教授, 博士生导师, 主要研究方向:微分方程理论及应用, Email:wengpx@scnu.edu.cn. 1000-5463(2010)03-0019-05 O175.14 A

























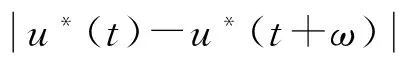

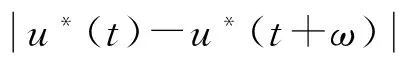














2 讨论










