基于LS-DYNA压力矫直钢管反弯挠度的计算

王志飞，田雅琴，黄庆学，王晓璐

(太原科技大学，山西 太原 030024)

1 前言

钢管在进行轧制或热处理后，由于受到外力、热应力或组织应力的影响，钢管不可避免地会出现弯曲变形，严重影响其后道工序的加工和产品质量，故对其进行矫直尤为重要。压力矫直法是以外加静载荷使钢管产生反向变形以达到矫直目的的一种方法，常用于对钢管端部、大直径钢管、低塑高强度钢管等矫直。随着生产发展的需要，国内钢铁企业对全自动液压矫直机的需求越来越大。所以，应积极开发创新技术附加值高的全自动压力矫直机系列及成套设备，完善检测和控制装置，以满足生产需要，为压力矫直工艺提供新的技术。因此对压力矫直参数的计算颇为重要，本文提出用有限元分析软件ANSYS/LS－DYNA计算压力矫直钢管反弯挠度的新方法。

2 曲率与反弯挠度计算

2.1 变形与曲率

对于斜辊矫直、平行辊矫直和压力矫直，在力学性能分析上可以将它们完全简化为集中载荷，和实际情况也相当吻合;在几何模型分析上可以从微小线段单元来考虑弯曲的曲率和变形，这样既接近于实际又对研究比较方便。本文从微小弧度段来分析弯曲时的曲率变化，其中工件原始状态呈弯曲态，具有原始弯曲半径ρ0，所对应弧心角为A0，管材的矫直曲率比方程式为

式中，C0为原始曲率比，C0=A0/At，A0为弧心角，A0=l/ρ0，At为弹性极限曲率角，At=2εt/H;H为断面高度;Cw为反弯曲率比，Cw=1/ρw; ρw为曲率半径;a=r/R。

2.2 曲率方程与挠度

2.3 反弯挠度

根据反弯挠度公式和曲率方程

其中，δw为弹性极限挠度，δt=l2Mt/(3EI)，I

根据曲率公式(3)得到反弯挠度δw，弯曲时的曲率变化如图1所示。

图1 弯曲时的曲率变化

根据公式(3)可知，反弯挠度δw需要通过弹性极限曲率角At计算，而极限曲率角At的公式计算中，需要确定参数断面高度H，弹性极限曲率角At为

式中，εt为弹性极限应变。

3 有限元计算过程

3.1 模型建立

依据有限元分析软件ANSYS建立模型如图2所示，单元为3Dsolid164;钢管为双线性随动强化模型，弹性模量E=150 GPa;泊松比P=0.35;切线模量为50 000 MPa。压头和支座为刚体模型，单元为3Dsolid164;弹性模量E=210 GPa;泊松比P=0.3。约束和加载:支座为全约束，压头只有Y方向可运动，接触面静摩擦系数为0.3，动摩擦系数为0.2，压下时间为10 s，反弯时间为5 s。

本文中采用手动定义，选用实体单元进行划分。整个钢管共划分出10600个单元，支座共划分出5180个单元，压头共划分出2570个单元。钢管建模及网格划分如图2所示。

图2 钢管压力矫直的模型

3.2 计算结果

经过矫直过程进行数值计算得到原始挠度δ0、压下挠度δ、反弯挠度δw的数据关系。计算不同厚径比和不同外径的多种型号钢管的挠度如表1～3所示。

表1 厚径比为0.2时挠度 mm

表2 厚径比为0.15时挠度 mm

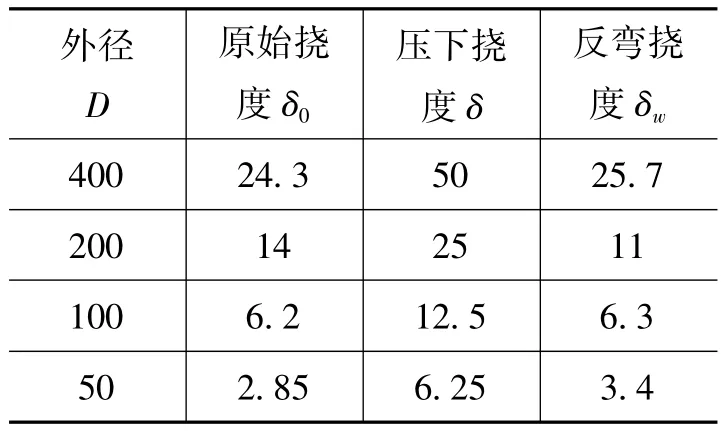
表3 厚径比为0.25时挠度 mm

图3为多组数据数值分析后的压下挠度－反弯挠度曲线图。

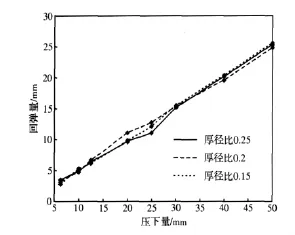
图3 压下矫直钢管压下挠度－反弯挠度曲线图

4 实验数据测试

4.1 测试实验数据

不同型号的钢管(以不同厚径比和不同外径)的反弯挠度如表4～6所示。

表4 厚径比0.2时挠度与断面高度 mm

表5 厚径比为0.15时挠度与断面高度 mm

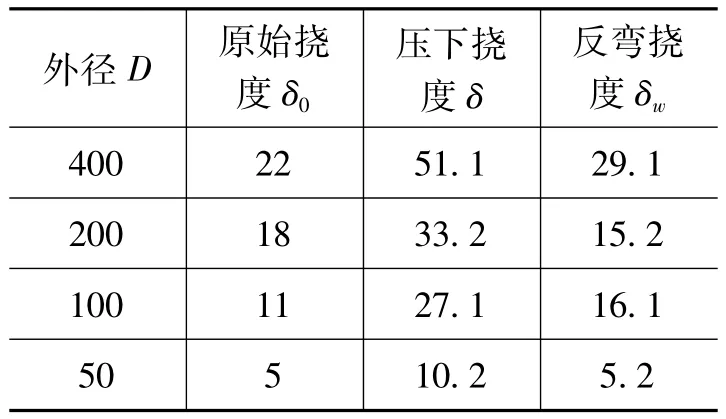
表6 厚径比为0.25时挠度 mm

4.2 仿真计算数据与实验数据对比

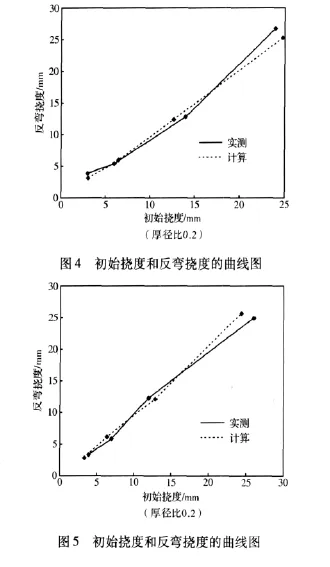
图4、图 5、图 6分别为厚径比是 0.2、0.15、0.25时仿真计算得到的挠度曲线与实测挠度曲线比较。图4、图5可以说明利用仿真计算得到δ0、压下挠度δ，反弯挠度δw与实测得到的数据基本一致的;图6波动较大，但整体趋势是一致的，这是由测试误差引起的。

5 结束语

以弹塑性理论和矫直理论为基础，用有元限仿真模拟钢管矫直，并分析计算了钢管的反弯挠度，计算结果和实验实测数据其中一致，证明了计算机仿真方法是正确的。为计算压力矫直钢管的参数计算提出了依据。

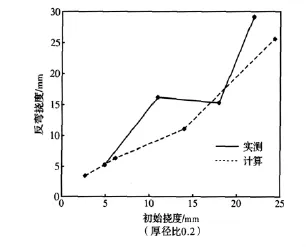
图6 初始挠度和反弯挠度的曲线图

［1］ 李俊．基于校直过程模型的校直工艺理论及实验研究［D］．上海:上海交通大学，2005．

［2］ 崔甫．矫直原理与矫直机械［M］．北京:冶金工业出版社，2002．

［3］ Kin Seung-Cheol，Chung Sung-Chong．Synthesis of the multi-step straighteness Control system for shaft straightening processes［J］．Mechatronics，2002，12:139－156．

［4］ LI Jun ZOU Huijun，XIONG Guoliang．Establishment and Application of Load-deflection Model of Press Straightening［J］．Key Engineering Materials Vols 2004．274－276．

［5］ 盛艳明，李俊．钢轨端部压力矫直的有限元分析［J］．重型机械，2007，(5)．