投资决策中NPV与IRR的矛盾性分析

耿秀艳

(北京物资学院,北京 101149)

投资决策中NPV与IRR的矛盾性分析

耿秀艳

(北京物资学院,北京 101149)

企业在进行投资决策时一般选用NPV和IRR等决策指标,而这两个指标在具体应用中会产生很多差异。从公式角度对两者产生矛盾的情况进行分析,认为产生矛盾的主要原因是本身的经济含义不同。再投资率的假设不同也是由于指标本身的定义引申出来的。在此基础上,对NPV和IRR进行总结,以便投资者对其有更本质的认识和应用。

NPV;IRR;矛盾性;再投资收益率

企业在进行投资决策时一般选用NPV和IRR等决策指标,而这两个指标在具体应用中会产生很多差异。从公式角度来看,产生矛盾的主要原因是本身的经济含义不同。再投资率的假设不同也是由于指标本身的定义引申出来的。根据一些调查NPV和IRR的使用很广泛,受到管理者的青睐。但是两者的优劣和其存在的矛盾一直是理论界进行讨论分析的热点。而且随着研究工作的深入,两者的缺陷逐步暴露出来,因此有必要对两者产生差异的原因进行研究,以便进行修正使之更好的为投资决策提供准确的预测分析。

一﹑从公式出发了解其基本概念和其经济含义

若想真正了解NPV与IRR的矛盾性,首先应该掌握各自的基本含义。

(一)NPV定义和公式

净现值(Net Present Value)是指项目从投资开始至寿命结束时一切现金流(包括现金流出和现金流入)的现值之和。计算公式为:

其中:CFt——第t年现金流(其中CF0为第一年现金流,即初始投资,CF0<0)

k——贴现率(企业要求的报酬率)

n——初始投资至项目结束时的年数

其经济含义:NPV反映企业在该项目上的绝对盈利能力,它实际上反映股东财富的增加或减少。NPV>0表示该项目可以获得比基准收益率更高的收益,可以接受; NPV=0表示项目产生的现金流刚好弥补了投资,可以接受;NPV<0表示项目不能接受。

(二)IRR定义和公式

内部报酬率(Internal Rate of Return)是指使项目的净现值等于零的贴现率。其公式为

其中:CFt——第t年的现金流(CF0为第一年现金流,即初始投资,CF0<0)

IRR——内部报酬率

n——初始投资至项目结束时的年数

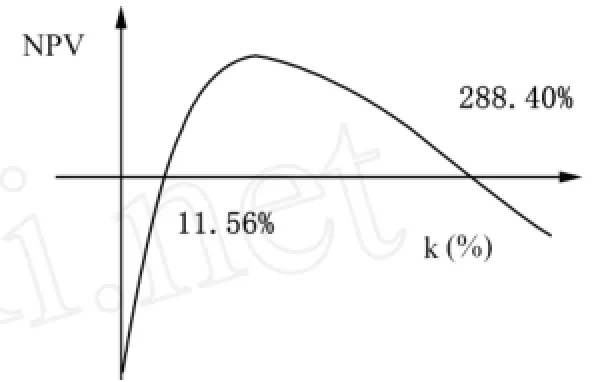
经济含义:IRR是以该项目所承担最高资本成本时体现的预期收益率,实际上动态反映了投资项目的真实报酬率。一般的说,IRR>k表示项目未来的内部报酬率大于企业的资本成本,其超出的部分在偿还成本后会留存,则企业可以接受;IRR=k表示预期收益率刚好弥补企业的资本成本,企业也可以接受;IRR

(三)从公式出发得出两者会产生矛盾的情形

由上述两公式可以看出,IRR公式是NPV公式的简化,两种方法使用同一个基本公式。只是在公式1中,贴现率k是指定的NPV是计算得出的,而公式2中,NPV为零计算IRR。

从数学角度看公式(-),不妨设X=(1+IRR)-1,得下列式子:

N次多项式,含N个根。其中X正实根的个数即为有意义的内部报酬率的数目。根据狄斯卡尔符号规则,正实根的个数不会超过方程式系数CF0,CF1,CF2……CFN中符号变更的次数。(如果有系数为零,可看作无符号)

因CF0<0,故其符号变更的次数≥1.(这里不考虑无根情况)

1.若变更一次,则IRR只有一个正实根,此时为常规项目,即初始投资后净现金流产生。对应于企业资金来源是否有限制,可以将常规项目分为:

(1)独立项目(相互独立的方案,投资资金没有限制):每个项目之间互不影响,只要符合要求,企业就会进行投资。对这类项目,采用NPV和IRR能得出完全一致的结论。此时可以运用净现值曲线分析,在某一确定的贴现率k0下,纵轴截距即表示在贴现率下净现值的数目,曲线与横轴的交点即为IRR。由此可见,只要NPV>0(方案可取),则选取的贴现率k0必定在IRR的左边,即IRR>k0,预期收益率高于贴现率,根据IRR的规则此方案也可取。

(2)互斥项目(投资资金受到限制,必须对项目进行排序,方便从中选择)下列两种情况会导致NPV曲线相交,使得两指标的结论产生矛盾:

第一种情况:初始投资规模不同。即项目的资本成本不同,这时采用NPV与IRR得出的结论是矛盾的。举个例子:

表1 项目A和B的现金流量表 单位:元

根据分析结果,如果采用NPV法,因NPVa>NPVb,应该选取A方案;若采用 IRR法,IRRa

第二种情况:现金流的发生时间不同。对于一些初始规模相同的项目,有的现金流发生在早期,有的发生在晚期。这种情况下运用两种方法得出的结论也是不一致的。现举例如下:

表2 项目C和D的现金流量表 单位:元

根据分析结果,如果采用NPV法,则项目D优于项目C,若采用IRR法,则项目C优于项目D。两者的排序是相反的。其净现值曲线如下图1。

图1 项目C和D的净现值曲线

由图可以看出,按照NPV法,“费希尔交点”ke左边,项目D优于项目C,ke右边,项目C优于项目D。而贴现率为10%,故D优于C,与IRR法矛盾。项目D的曲线比项目C的曲线要陡,说明贴现率的变化对D的影响要比C大。由公式可以推导分析,D的的现金流多产生于后期,贴现率对其更有影响,因此其曲线更具敏感性。

2.变更多次——IRR有多重根,为非常规项目。即项目在经过初始投资产生正的现金流后,又因为其他原因产生负的现金流,或者发生多次反复的情况,比如项目中间增加投资,发生维修费用,项目结束时需要支出清理费等。这种非常规项目,实际上会有两个或两个以上的内部报酬率,即多重内部报酬率(Multiple IRRs).此时投资者将无法正确选用项目,指标失效。NPV就不会遇到这种情况。如下例子:

其NPV曲线如下图2。

由图可以看出,在贴现率为10%的情况下,NPV =-103(元),此时应拒绝项目。而在 IRR下,只要贴现率在11.56%—288.4%之间,净现值为正,可以接受项目,否则拒绝。这种情况下两者也会产生矛盾,采用 IRR要比NPV复杂的多,且准确性很差,人们往往容易把碰到的第一个正解当做唯一解进行判断,容易误导投资者。

表3 项目E的现金流量表 单位:元

图2 项目E的净现值曲线

二、关于两者矛盾性的原因分析及其结论

根据上述分析,可以看出NPV与IRR的基本公式是一致的,这两个评价标准是紧密联系的。之所以会出现矛盾性,是因为两者不同的的经济含义导致两者的计算模式、计算理念不同。一个是绝对指标,一个是相对指标,由公式会得出不同的结论。对于NPV的计算公式,其中贴现率k是固定的,而所要求的IRR即是使NPV等于零的临界贴现率。两者出现矛盾性的直接原因就是贴现率k的不同。由此引出了一个经典问题:这两个指标隐含着不同的再投资假设—NPV中假设再投资收益率为其资本成本率,IRR法假设企业以其内部报酬率进行再投资。这些假设在对指标的使用、推导过程中起一定的作用,所以针对上述不同的情形,会得出不同的结论。

不论是NPV、IRR还是投资回收期等其他投资决策指标,对于投资者来说不同的指标提供了不同类型的信息,因此单纯用一种方法对投资项目进行分析是很不全面的。这些指标只是运用数学方法对投资项目进行量化分析,而制定决策要考虑很多定性因素,比如公司的战略、公共关系,营销策略,财务成本等其他很多方面。这些复杂的情况使得管理者在运用指标的时候更要谨慎、认真。

[1] 杨充霖,文先明.净贴现值和内在收益率的非自洽性及其深层原因研究[J].系统工程,2003(2).

[2] 吕长江.净现值法和内含报酬率法冲突的协调[J].数量经济技术经济研究,1998(4).

[3] 王士伟.NPV与IRR的一致性及矛盾性分析[J].会计之友,2009(5).

[4] 李海涛,陈通,王迎秋.再论净现值与内部收益率非自洽性的原因[J].西北农林科技大学学报,2008(1).

[5] 尤金·F·布里格姆,菲利普·R·戴夫斯.中级财务管理[M].王化成,黄磊,译.北京:中国人民大学出版社,2009.

F283

A

1671-8275(2010)04-0025-02

2010-03-15

耿秀艳(1986-),女,山东宁阳人,北京物资学院硕士研究生。研究方向:财务管理。

责任编辑:何玉付