一种多属性和准则定序分类模型

朱颢东，钟 勇

(1.中国科学院 成都计算机应用研究所，成都610041，zhuhaodong80@163.com;2.中国科学院 研究生院，北京100039)

多属性和准则定序分类是现实生活中一类重要的决策问题［1-2］，对于该问题的现有解决方法在获取决策者的偏好信息方面都存在困难.关系模型和函数模型是解决该方法的主要模型，但是这两个模型需要事先给出较多的偏好信息，例如准则权重、满意度等［3-4］，这为那些不熟悉这两个模型的用户增加了难度.粗糙集理论的出现为这类问题提供了较为可行的解决办法［5］.但是粗糙集理论是利用不可区分关系来解决问题的，但它在解决多属性和准则定序分类问题时能力较弱.Greco 等［6-9］学者使用优势关系来代替不可区分关系以增强粗糙集解决多属性和准则定序分类问题的能力，但也存在一定的局限性.本文在这些文献的基础上，对经典粗糙集理论进行了扩展，并给出了一个基于扩展粗糙集的决策分析方法.该方法使用“不可区分-相似-优势”关系来代替经典粗糙集理论中的不可区分关系来获取知识的粗糙近似.

1 一种新的不一致问题

经典粗糙集方法是通过不可区分关系来实现知识的获取，每个非空的属性子集P 都对应着U上的一个不可区分关系，记作IP:IP={(x，y)∈U×U:q(x)=q(y)，∀q ∈P}，如果(x，y)∈IP，则称x 和y 是p 不可区分的，这样定义的不可区分关系是一种等价关系，即满足自反性、对称性、传递性.关系IP的所有等价类的集合记作U/IP(形成U 上的一个划分).关系IP中的等价类称为P 初等集.对于由信息粒度引起的不一致问题，经典粗糙集理论是可以解决的，但是有准则属性出现时，需要在数据分析时考虑优势关系.

以公司进行破产风险评估作为例子.其中，用一个准则(投资回报)和一个属性(所在城市)来描述该公司.

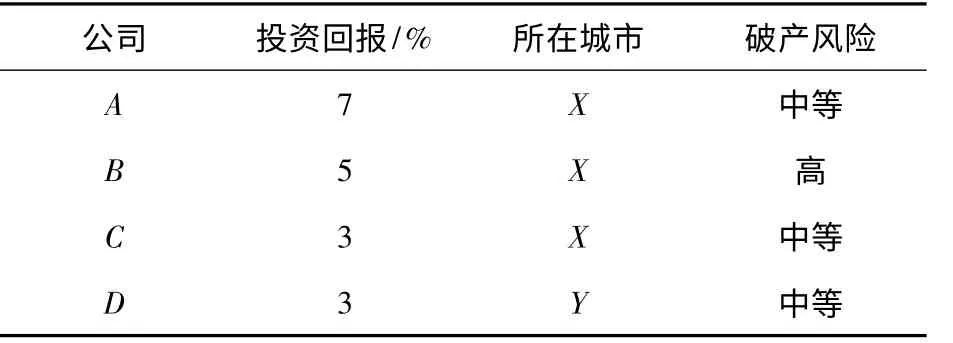
表1 破产风险评估表

表1 表明:因为A 的投资回报高于B 的投资回报，而A 的风险低于B 的风险，并且它们所在城市相同，因此A 的评估结果比B 的评估结果好，这是合理的.D 的评估结果也比B 的评估结果好，虽然B 的投资回报较高，但是B 和D 位于不同的城市，其投资条件可能不同，此结果并不违背优势原理.C 的评估结果好于B 的评估结果，虽然B 的投资回报较高，但是C 和B 处在相同的城市，评估结果违背了优势原理，使得B 和C 是一对不一致样本.

2 对经典粗糙集的扩展

2.1 对优势关系的扩展

已知S= ( U ，C ∪D，V，f)，其中，C～为定量属性子集为定性属性子集，C＞为准则子集，则且此外，对任意的P ⊆C，记

1)对∀q ∈C～，Rq为U 上一个相似关系，xRqy 为在定量属性 q 上 x 相似于为给 定的阈值 ).若∀x，y ∈U，∀q ∈P～⊆C～，有xRqy，则在P～上x 相似于y.

2)对∀q ∈C＞，Sq为U 上一个优势关系，xSqy 在准则属性q 上x 至少同y 一样好(f(x，q)≥f(y，q)).若，有xSqy，则在P＞上x 优于y.

3)对∀q ∈C≡，Iq为U 上一个不可区分关系，xIqy 为在定性属性q 上x 同y 不可区分(f(x，q)=f(y，q)).若∀x，y ∈U，∀q ∈，有xIqy，则在上x 和y 不可区分.

另外，如果决策属性集D 把论域U 划分为若干个决策类，令cl={clt|t ∈T，T=1，2，…，n}，为决策类集合，那么∀x ∈U 且仅属于一个clt∈cl，而且∀r，s ∈T，若r ＞s，则clr中的对象(严格地或弱地)优于cls的对象.定义［x ∈clr，y ∈cls，r ＞s］⇒［xSy］，其中，xSy 为x 不劣于y.由于决策类的这种偏好序关系，令={x|(x ∈clt)∨(∀y ∈clt∧xSy)}称为决策类clt的向上并集，称为决策类clt的向下并集，即.显然，

2.2 新的粗糙近似

经典粗糙集是用一种知识近似另一种知识，其中被近似的知识是决策属性集D 划分U 所形成的决策类，用于近似的知识是条件属性集C 划分U 所形成的基本集.但对定序分类而言，不但决策类具有偏好序，而且条件属性集含有准则，此时被近似的知识是决策类的向上并集和向下并集，用于近似的知识不再是仅由不可区分关系定义的对象集，而是由相似、优势和不可区分关系共通定义的对象集，这也是扩展方法与经典方法的主要区别.

对于∀P ⊆C，定义DP和为U 上的两个自反二元关系，称为“不可区分-相似-优势”关系，对∀x，y ∈U:①xDPy iff ∀q ∈P＞，xSqy;∀q ∈，xIqy ∧∀q ∈P～，yRqx.②iff∀q ∈P＞，xSqy;∀q ∈，xIqy ∧∀q ∈P～，xRqy.

给定P ⊆C，x ∈U，扩展方法中，用于近似的“知识粒”为:

1)在P＞上，y 优于x;在上，y 和x 不可区分;在P～上，x 相似于y 的对象y 的集合(x)={y ∈U:yDPx}.

2)在P＞上，y 优于x;在P≡上，y 和x 不可区分;在P～上，y 相似于x 的对象y 的集合:(x)={y ∈U}.

3)在P＞上，y 劣于x;在P≡上，y 和x 不可区分;在P～上，x 相似于y 的对象y 的集合(x)={y ∈U:}.

4)在P＞上，y 劣于x;在P≡上，y 和x 不可区分;在P～上，y 相似于x 的对象y 的集合(x)={y ∈U:xDPy}.

所以，∀P ⊆C，必定属于cl≥t 的全部对象形成了的P-下近似，记作)={x ∈U:;可能属于的全部对象形成了的P-上近似，记作t=1，2，…，n.类似地，可以定义的P-下近似和P-上近似.因此，决策类的边界为:∀P ⊆C，定义和的关于P 的近似精度为

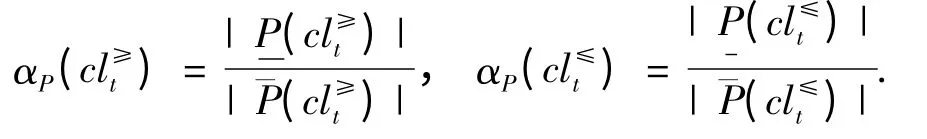
此近似精度描述的是利用P 对对象分类时可能决策中正确决策的百分比.

定义 划分cl 关于P 的近似分类质量为

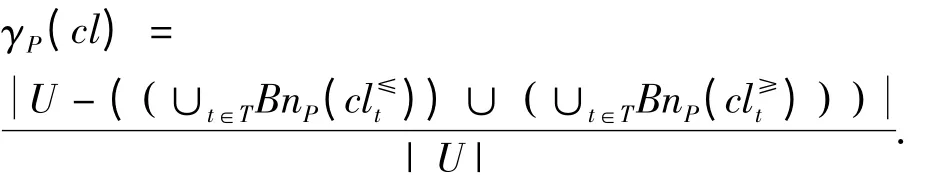
式中:P 能确切地划入cl 类的对象的百分比.

条件属性集C 的最小子集P ⊆C 称为决策表的一个约简，当且仅当γP(cl)=γC(cl).一个决策表可能有多个约简.

2.3 提取决策规则

由决策类的向上和向下并集的粗糙近似，可以获得3 类决策规则:

1)D≥-决策规则，由形成:若f(x，q1)≥rq1，…，f(x，qu)≥rqu且f(x，qu+1)=rqu+1，…，f(x，qv)=rqv且f(x，qv+1)相似于rqv+1，…，f(x，qz)相似于rqz，则x ∈;其中，P={q1，…，qz}⊆C，P＞={q1，…，qu}，={qu+1，…，qv}，P～={qv+1，…，qz}，{rq1，…，rqz}∈Vq1×Vq2×…×Vqz，t ∈T;

2)D≤-决策规则，由形成:若f(x，q1)≤rq1，…，f(x，qu)≤rqu且f(x，qu+1)=rqu+1，…，f(x，qv)=rqv且f(x，qv+1)相似于rqv+1，…，f(x，qz)相似于rqz，则x ∈;其中，P={q1，…，qz}⊆C，P＞={q1，…，qu}，P≡={qu+1，…，qv}，P～={qv+1，…，qz}，{rq1，…，rqz}∈Vq1×Vq2×…×Vqz，t ∈T;

3)D≥≤-决策规则，由形成:若f(x，q1)≥rq1，…，f(x，qu)≥rqu且f(x，qu+1)≤rqu+1，…，f(x，qv)≤rqv…，f(x，qv)=rqv且f(x，qv+1)=rqv+1，…，f(x，qw)=rqw且f(x，qw+1)相似于rqw+1，…，f(x，qz)相似于rqz，则x∈cls∪cls+1∪…∪clt;其中，P={q1，…，qz}⊆C，P＞={q1，…，qu}∪{qu+1，…，qv}，={qv+1，…，qw}，P～={qw+1，…，qz}，{rq1，…，rqz}∈Vq1×Vq2×…×Vqz，s，t ∈T，s ＜t，{q1，…，qu}和{qu+1，…，qv}能够相交.

3 实例验证

表2 是一个决策表，其中有8 家商场作为决策对象，其中，A1为交通条件、A2为位置、A3为面积，m2、A4为商场内环境、A5为同类商品平均价格、A6为服务态度、A7为客流量，d 为决策属性.表2 中d 把论域划分为赢利、盈亏平衡、亏损3 类.

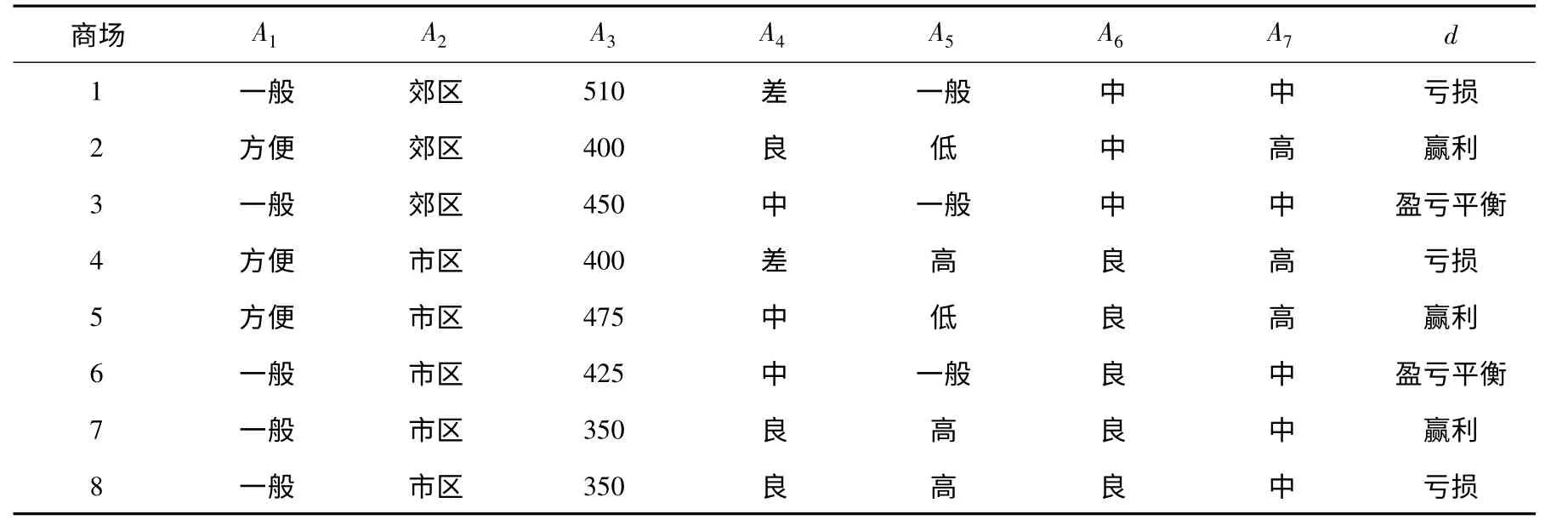
表2 一个具有多属性和准则的决策表

3.1 经典粗糙集方法的结果

显 然，C = {A1，A2，A3，A4，A5，A6，A7}，D ={d}.其中，cl1为亏损的商场类，cl2为盈亏平衡的商场类，cl3为赢利的商场类.cl1={1，4，8}，cl2={3，6}，cl3={2，5，7}.cl1，cl2，cl3的C-下近似、C-上近似、C-边界分别为，BnC(cl1)={7，8={3，6}(cl2)={3，6}，BnC(cl2)=φ={2，5})={2，5，7，8}，BnC(cl3)={7，8}.

因此，cl1，cl2，cl3的近似精度分别为0.5，1，0.5.分类质量为0.75.存在约简{A2，A3}或{A3，A6}.

以约简集{A3，A6}为例，可以得到的最小决策规则集为(其中:(x，A3)，(x，A6)为支持对应规则的对象，(1，…，8)为所对应的商场):

1)若f(x，A3)=510，则x ∈cl1(1).

2)若f(x，A3)=450，则x ∈cl2(3).

3)若f(x，A3)=475，则x ∈cl3(5).

4)若f(x，A3)=425，则x ∈cl2(6).

5)若f(x，A3)=400，f(x，A6)=“中”，则x ∈cl3(2).

6)若f(x，A3)=400，f(x，A6)=“良”，则x ∈cl1(4).

7)若f(x，A3)=350，则x ∈cl1或x ∈cl3(7，8).

3.2 使用“不可区分－相似－优势”关系的近似结果

同样是C ={A1，A2，A3，A4，A5，A6，A7}，D ={d}，但观察到A1或A7是一个准则属性.对A1来讲，“方便”优“一般”.而对A2、A3来讲，它们再相关域上不存在优势关系.对属性A2而言，使用经典的不可区分关系，即∀x，y ∈U，xIqy，则有f(x，A2)=f(y，A2).对属性A3来说，定义一个相似关系， 使 得 ∀x，y ∈ U，xRqy， 则 有.因为考虑了3 个决7}，它们的C-下近似、C-上近似、C-边界分别为= {1，4，6，7，8}，策类，所以需要近似{1，4，8}= cl1∪ cl2= {1，3，4，6，8}，=cl2∪cl3={2，3，5，6，7}=cl3={2，5，={1，3，4，6}，={7，8}，= {2，3，4，5，6，7，8}，)= {2，5}，= {7，8}.的近似精度分别为0.2、0.67、0.43、0.5，而分类质量为0.5.存在约简{A2，A3}或{A3，A6}.

以{A3，A6}和准则属性A1为例，则可获得最小决策规则集(其中，(x，A3)，(x，A6)为支持对应规则的对象，(1，…，8)为所对应的商场):

1)若f(x，A3)为“中”，f(x，A3)相似于510，则

2)若f(x，A1)至少为“方便”，f(x，A6)为“中”，则

3)若f(x，A6)为“中”，f(x，A3)相似于450，则x ∈cl2(3).

4)若f(x，A6)为“良”，f(x，A3)相似于400，则x ∈cl1∪cl2(4，6).

5)若f(x，A1)至少为“方便”，f(x，A3)相似于475，则

6)若f(x，A3)相似于350，则x ∈cl1∪cl2∪cl3(7，8).

3.3 结果对比

仅使用不可区分关系时，近似分类质量为0.75，这是因为商场7、8 是不可区分的却属于不同的决策类.使用不可区分-相似-优势关系时，近似分类质量为0.5，这是因为商场4、6 存在不一致:在准则属性A1上，商场4 优于商场6;在属性A2上，商场4 和商场6 是不可区分的;在属性A3上，商场6 相似于商场4，因此有4DC6(同时也因商场4 相似于商场6，也有).可是，对商场4 的综合评估为亏损，对商场6 的综合评估为盈亏平衡，商场4 劣于商场6，这明显不符合优势原理.仅使用不可区分关系对这种不一致无能为力，而利用“不可区分-相似-优势”关系却可以揭示这种不一致.

4 结 论

1)经典粗糙集中的不可区分关系对解决多属性和准则定序分类问题能力较弱.

2)本文把经典粗糙集中的不可区分关系扩展为“不可区分-相似-优势”关系，实例表明该关系不但能够解决此问题而且还能处理决策表中可能存在的不一致现象，同经典粗糙集中的不可区分关系相比具有较好的有效性与优越性.

［1］GRECO S，MATARAZZO B，SLOWINSKI R.Rough sets theory for multicriteria decision analysis［J］.European Journal of Operational Research，2001，129(1):1-47.

［2］GRECO S，MATARAZZO B，SLOWINSKI R.Rough sets methodology for problems in presence of multiple attributes and criteria［J］.European Journal of Operational Research，2002，138(2):247-259.

［3］BELACEL N.Multicriteria assignment method:Methodology and medical applications［J］.European Journal of Operational Research，2000，125(1):175-183.

［4］ZOPOUNIDIS C，DOUMPOS M.Multicriteria classification and sorting methods:A literature review［J］.European Journal of Operational Research，2002，138(2):229-246.

［5］胡寿松，何亚群.粗糙决策理论与应用［M］.北京:北京航空航天大学出版社，2006:23-33.

［6］GRECO S，SLOWINSKI R，STEFANOWSKI J，et al.Incremental versus non-incremental rule induction for multicriteria classification［C］//Transactions on Rough Sets II.Berlin Heidelberg:Springer-Verlag，2004:33-53.

［7］DEMBCZYNSKI K，GRECO S，SLOWINSKI R.Secondorder rough approximations in multi-criteria classification with imprecise e-valuations and assignments［C］//RSFDGRC 2005.Berlin Heidelberg:Springer-Verlag，2005:54-63.

［8］BLASZCZYNSKI J，DEMBCZYNSKI K，SLOWINSKI R.Interactive analysis of preference-ordered data using dominance-based rough set approach［C］//ICAISC 2006.Berlin Heidelberg:Springer-Verlag，2006:489-498.

［9］ZARAS K，THIBAULT J.Ranking by rough approximation of preferences for decision engineering applications［C］//RSKT2007.Berlin Heidelberg:Springer-Verlag，2007:142-148.

［10］LI Ming，ZHANG Baowei，WANG Tong，et al.Approximation of class unions based dominance-matrix within dominance-based rough set approach［C］//ACII2005.Berlin Heidelberg:Springer-Verlag，2005:795-802.

［11］ZARAS K.Rough approximation of a preference relation by a multi-attribute stochastic dominance for determinist and stochastic and fuzzy problems［J］.European Journal of Operational Research，2004，159(1):196-206.

［12］SHAO Mingwen，ZHANG Wenxiu.Dominance relation and rules in an incomplete ordered information system［J］.International Journal of Intelligent Systems，2005，20(1):13-27.

［13］JIA Xiuyi，SHANG Lin，JI Yangsheng，et al.An incremental updating algorithm for core computing in dominance-based rough set model［C］//RSFDGrC2007.Berlin Heidelberg:Springer-Verlag，2007:403-410.

［14］YUE Chaoyuan，YAO Shengbao，ZHANG Peng，et al.Rough approximation of a preference relation for stochastic multi-attribute decision problems［C］//FSKD 2005.Berlin Heidelberg:Springer-Verlag，2005:242-1245.

［15］桂现才.优势关系下信息系统的信息量与粗糙熵［J］.计算机工程与设计，2008，29(24):6340-6343.

［16］贾修一，于绍越，商琳，等.基于优势关系的粗糙集应用研究［J］.计算机科学，2008，35(8):901-904.

［17］徐伟华，张文修.基于优势关系下信息系统分配约简的矩阵算法［J］.计算机工程，2007，33(14):4-7.

［18］袁修久，何华灿.优势关系下的相容约简和下近似约简［J］.西北工业大学学报，2006，24(5):604-608.

［19］赵越岭，王建辉，顾树生.基于优势关系粗糙集的数据分类［J］.控制工程，2007，14(3):51-54.