基于条件方程的方差分量估计公式

梁 霄

(同济大学 测量与国土信息工程系,上海 200092)

基于条件方程的方差分量估计公式

梁 霄

(同济大学 测量与国土信息工程系,上海 200092)

著名的 Helmert方差分量估计公式是基于间接观测平差模型导出的。基于条件观测平差模型导出了方差分量估计公式并给出了实际应用范例,且对两种模型的方差分量估计公式的等价性进行了理论证明。算例表明,文中的估计公式能正确地估计出各类观测值的方差因子。

方差分量估计;条件方程;Helmert公式

Helmert在1907年导出了著名的方差分量估计公式,100多年来广泛用于不同类型观测值的精度估计,1979年Forstner对这一公式进行了简化。其它类型的方差分量估计公式,如M IN IQUE公式[1](Rao,1971)和B IQUE公式[2](Koch,1980),在观测值独立时,与 Helmert公式都是等价的。

由于Helmert公式是基于间接观测平差模型导出的,公式中需求逆运算的矩阵与未知参数数目相同,如果观测方程的参数比较多,势必影响计算效率。当条件方程数目少于未知参数时,如果使用基于条件方程的方差分量估计公式,有望提高解算效率。更加重要的是,条件平差是一种重要的平差模型,给出基于这一模型的方差分量估计公式在理论和实际上的应用是必要的。

1 基于条件平差的方差分量估计

1.1 方差分量估计公式

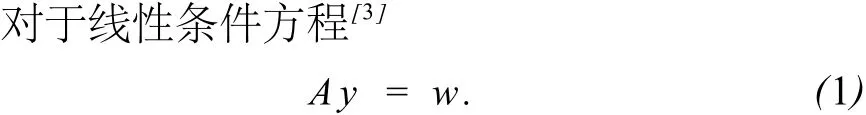
式中:A为r×n阶系数矩阵,y为 n×1阶观测向量,w为r×1阶闭合差向量。若将观测值表示成

式中:¯y为观测值真值,ε为观测误差。则有

因此,误差方程通常表示为

其中,v为观测值的改正数。

根据最小二乘准则

其中,Q为观测值的先验权逆阵。可得到,方程(1)的解为

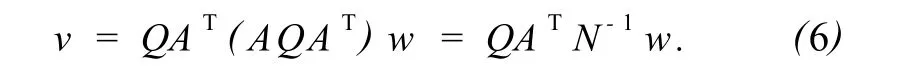
其中,N=AQAT。

将式(3)代入式(6)得

1.2 精度评定

1.3 基于条件方程与基于间接方程的方差分量估计的等价性证明可得,G阵与 F阵等价。同时,可看出,p阵和q阵完全相同。所以可得出结论,基于条件观测平差模型导出的方差分量估计公式与基于间接观测平差模型的方差分量估计公式是完全等价的。

2 算例分析

有边角网如图1所示,A、B、C为已知点,P1、P2为待定点,网中观测了12个角度和6个边长,起算数据和观测值见参考文献[8]第82页。根据经验,测角中误差为 ±1.5″,边长测量中误差±2.0 cm,现对其按条件平差和间接平差分别进行方差分量估计,比较平差结果的差异。计算结果如表1和表2所示。

图1 边角网

表1 基于条件平差的方差分量估计结果

表2 基于间接平差的方差分量估计结果

基于条件平差算出的单位权中误差的估值为±1.88″,方差分量估计的精度分别为var(σ^20β)=2.91″4和var(σ^20s)=8.24″4;基于间接平差算出的单位权中误差的估值为±1.88″,方差分量估计的精度分别为var(σ^20β)=2.92″4和var(σ^20β)=8.22″4。对比表1和表2对应位置的数据,忽略计算误差,以上的计算结果都与间接平差模型的方差分量估计的结果一致,由此可见,基于条件观测平差模型导出的方差分量估计公式是正确的,并与基于间接观测平差模型的方差分量估计公式是等价的。

3 结束语

本文从条件平差的基本理论出发,详尽地导出了不同于间接平差模型的方差分量估计公式,扩展了 Helmert方差分量估计的应用范围,证明了两种模型的方差分量估计公式的等价性,具有较好的应用前景,尤其是在条件数少于未知数的情况下,使用基于条件平差的方差分量估计可以简化计算过程。实验数据表明本文方法与间接平差的 Helmert方差分量估计公式完全等价。

[1]RAO.C.R.Linear Statistical Inference and Its App lications[D].New York Wiley,1973.

[2]KOCH.K.R.Parametersch(a)tung Und Hypotherentests in Linearen Modellen[D].Dümm ler,1980.

[3]於宗俦,于正林.测量平差原理[M].武汉:武汉测绘科技大学出版社,1990.

[4]陶本藻.测量数据统计分析[M].北京:测绘出版社,1992.

[5]党涌诗.矩阵论及其在测绘中的应用[M].北京:测绘出版社,1980.

[6]于正林,陈惠明.方差分量估计中的精度评定[J].测绘学报,1989,18(3):219-226.

[7]李博峰,沈云中,楼立志.基于等效残差的方差协方差分量估计[J].测绘学报,2010,39(4):349-354.

[8]崔希璋,於宗俦,陶本藻,等.广义测量平差[M].武汉:武汉测绘科技大学出版社,2001.

The variance component estimation formula based on conditional equation

L IANG Xiao
(Department of Surveying and Geo-informatics Engineering,Tongji University,Shanghai 200092,China)

The famous Helmert formula of variance component estimation was derived based on indirect observational equation.Thispaper derives the variance component estimation formula based on conditional equation and show s the p ractical app lications,p roves the equivalence between the two variance component estimation fo rm ulas based on indirect observational and conditional equations.The numerical case show s that our fo rmula can co rrectly estimate the variance components of different kind of observables.

variance component estimation;conditional equation;Helmert fo rm ula

P207

A

1006-7949(2010)06-0028-03

2010-05-07

梁 霄(1984-),女,硕士研究生.

[责任编辑张德福]