基于节约里程法的连锁超市配送线路优化设计

○黄春兰 李珊珊

（南京信息职业技术学院 江苏南京 210046）

基于节约里程法的连锁超市配送线路优化设计

○黄春兰 李珊珊

（南京信息职业技术学院 江苏南京 210046）

近年来，大大小小的连锁超市在我国各地得到了长足的发展，连锁超市之间的竞争激烈化程度开始加剧。连锁超市要在激烈竞争的市场中取胜，必须改进物流现状，重视配送中心的作用，降低物流成本以加强供应链的保障能力，快速响应顾客的需要。如何更好地设计或者优化现有的配送线路，成了一个难题，文章将对这个问题进行研究。

连锁超市 配送线路 优化设计 节约里程法

一、问题的提出

物流配送是社会化大生产、国民经济发展的客观要求，它的发展状况对城市经济发展、商品流通和大众消费起着重要的促进或制约作用。而好的配送方案，不仅能够节约物流成本，提高商品运动的速度，而且还由于它能有效连接生产与消费，从而既有利于物流服务和商品附加价值的实现，又能有效促进生产商按需生产，真正使物流的管理建立在实需经营的基础上。由于配送独有的特点，合理规划配送路线对配送成本的影响非常显著，所以必须在全面计划的基础上，制定高效的配送路线，这也是整个配送系统优化的关键环节。

在配送路线选择中，主要采取模型化方法进行路线确定。常见的模型有Tabu Search算法、SOM方法、遗传算法、节约里程法等。节约里程法，又称车辆运行计划法（VSP-Vehicles Scheduling Program），适用于实际工作中要求得较优解或最优的近似解，而不一定需要求得最优解的情况。它的基本原理是三角形的一边之长必定小于另外两边之和。当配送中心与用户呈三角形关系时，由配送中心P单独向两个用户A和B往返配货的车辆运行距离必须大于以配送中心P巡回向两用户发货的距离。那么，所计算的结果：2Lpa+2Lpb-（Lpa+Lpb+Lab）=Lpa+Lpb-Lab为巡回发货比往返发货的节约里程。

本文根据连锁超市配送特征，选择节约里程法模型进行配送路线设计。

二、研究对象的选取

根据中国连锁经营协会数据显示，2007年国内零售业巨头苏果超市的苏果马群物流配送中心占地面积17万平方米，单体仓库面积达4.2万平方米，为华东地区第一，年配送额可达60亿元，有效配送半径为300公里。本文即选择苏果马群物流配送中心为研究对象，基于节约里程法对配送中心到周边若干门店的配送路线进行设计。

三、模型的假设

假设对于选定的一些超市进行分析，而不是对所有的超市进行分析；假设针对超市某一类的货物分析而不是所有物品进行分析；假设每个客户只能被访问一次，每辆车其能服务一条路线，在配送中心装货后，在每一站依次卸货；假定目标是使系统运作费用最小，为简化，假设为配送的总路程最小。

四、用于分析的数据

本文选择南京马群周边的12个苏果超市（见表1）。

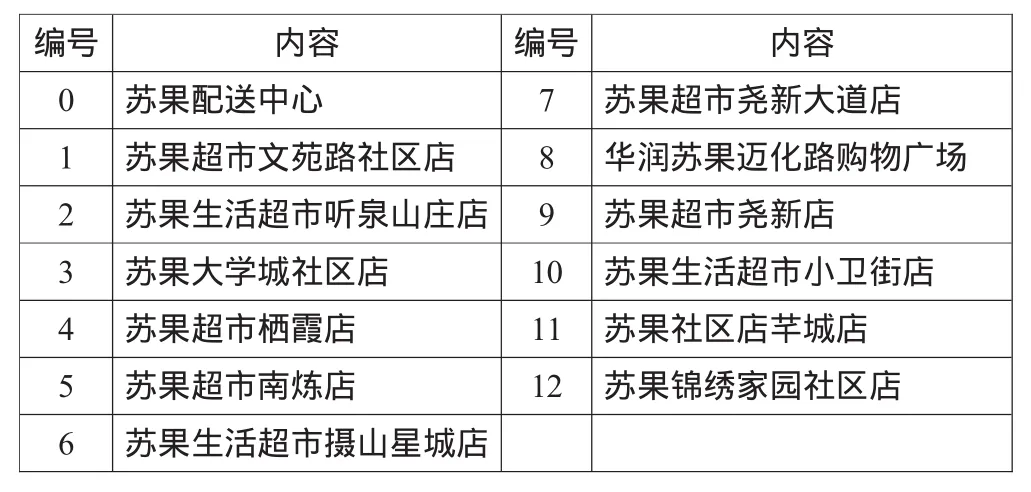
表1

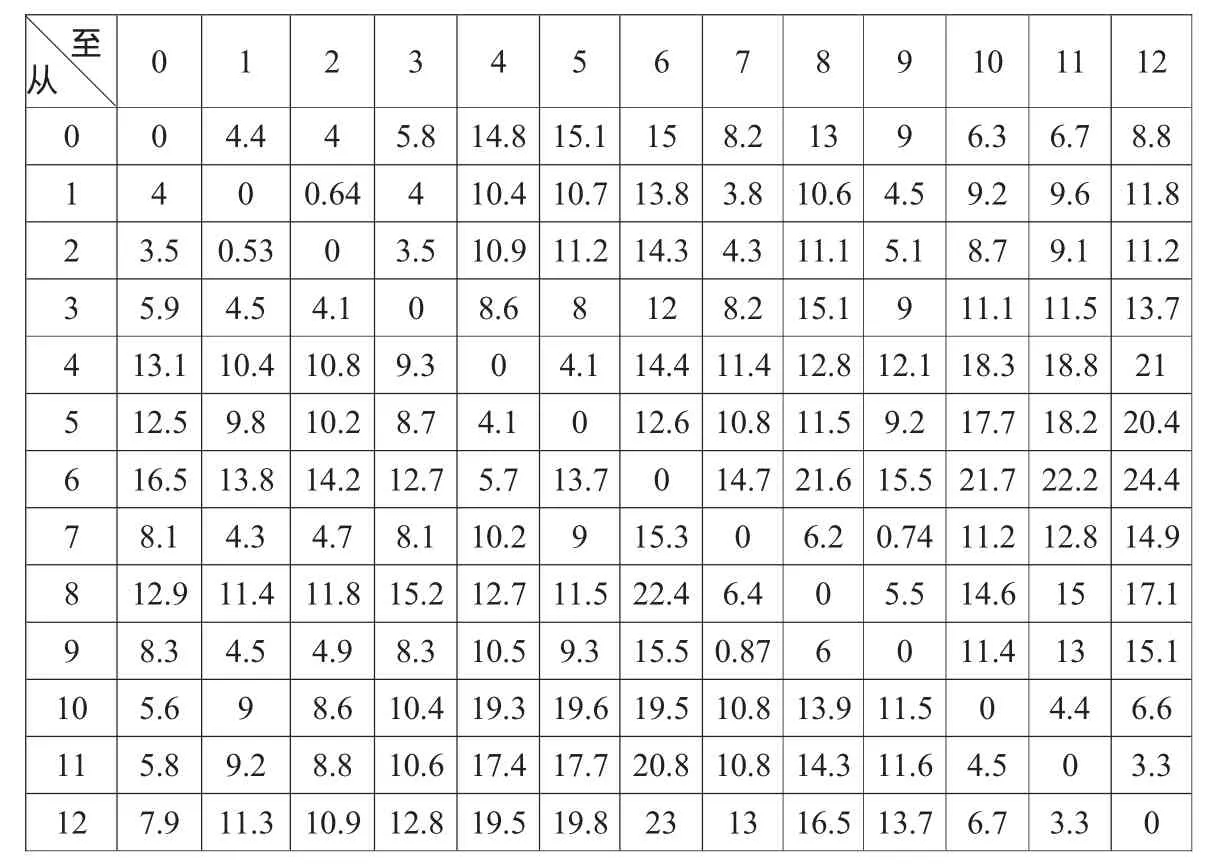
表2 里程表（单位：千米）

表1中编号0代表的是苏果马群配送中心，之后的依次是12个门店。

接下来统计各门店之间的距离，本文借助的是百度地图的距离查询功能，依次查询之后得到相互之间的距离：由于马路的双向性，所以往返的里程是不相同的。虽然差距并不会太大，但是我们还是把它们区别对待。最终，得出了里程表（表2）。

根据这个里程表，我们就可以使用节约里程法进行线路的优化设计。

五、使用节约里程法进行线路优化设计

节约里程法，又称C-W算法，是由Clarke和Wright于1964年首次提出的。它的基本思想就是：对于配送中心以及两个门店，关系如图1所示。

图1

如果车辆从 P-＞A-＞P-＞B-＞P，所需要的距离为 dis[P，A]+dis[A，P]+dis[P，B]+dis[B，P]，而如果我们把路线改为，P-＞A-＞B-＞P 的话，则总距离为 dis[P，A]+dis[A，B]+dis[P，B]，节约的路程为 dis[A，B]-dis[A，P]-dis[P，B]，我们把这个路程记作“节约值”s[A，B]。我们知道从A至B的距离一定存在一个先开到P点再开到B点的路程选择，距离为dis[A，P]+dis[P，B]，但这个未必是最优的，换言 s[A，B]=dis[A，B]-dis[A，P]-dis[P，B]应该≥0。

据此，我们可以设计出具体的算法：

Step 1：读入两两之间的距离，填入dis数组中；Step 2：求出所有门店之间的节约值s[A，B]；Step 3：然后按节约的值从大至小排序；Step 4：从第一辆车开始设计，对于每辆车；Step 4.1：初始路线为空；Step 4.2：找到最节约的s[A，B]，构造路线 0-＞A-＞B-＞0（0为配送中心）；Step 4.3：在s中划去从A出发的以及到达B的元素，即划去s[A，X]与 s[X，B]，X 为任意值；Step 4.4：若当前的路线为0-＞X-＞……-＞Y-＞0，我们找到最节约的 s[A，B]，使得B=X或A=Y，对于构造出路线0-＞B-＞X-＞……-＞Y-＞0或 0-＞X-＞……-＞Y-＞A-＞0；Step 4.5：在 s中划去从A出发的以及到达B的元素，即划去s[A，X]与s[X，B]，X为任意值；Step 4.6：如果当前车承载的超市数已达上线转Step4重新设计下一辆车；Step 4.7：转Step4.4；Step 5：设计好每辆车的配送路线，算法结束。

六、程序求解

对于这个算法，我们编写对应的C#程序进行求解，运行程序，得到节约里程表按从大至小的排序后如表3所示。

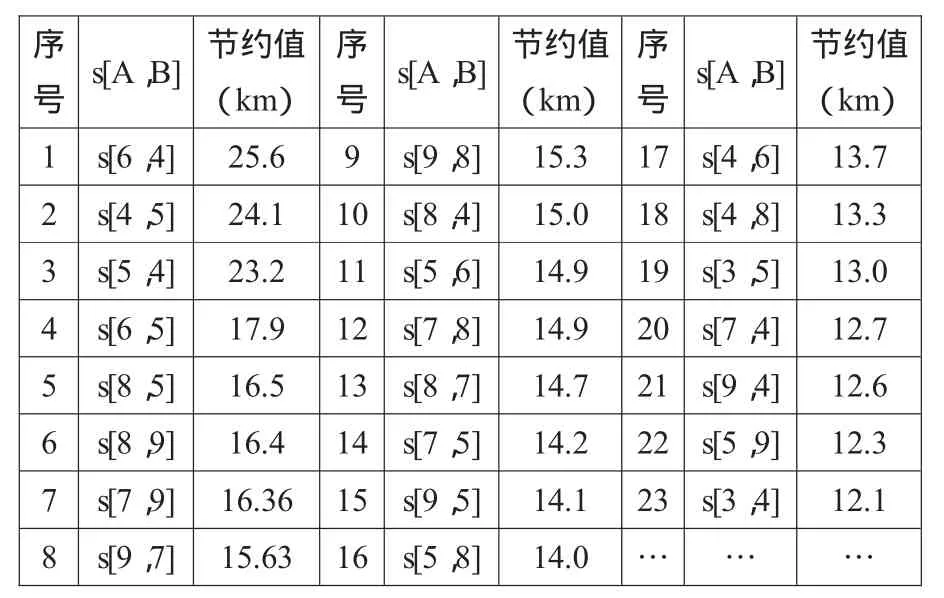
表3

而我们知道，未优化的配送总距离215.2千米。

当每车需承担2个超市的时候，程序的计算过程为：车1：合并路线 0-＞6-＞4-＞0，总里程 33.8，节约里程 25.6；车 2：合并路线 0-＞8-＞5-＞0，总里程 37.0，节约里程 16.5；车 3：合并路线0-＞7-＞9-＞0，总里程 17.24，节约里程 16.36；车 4：合并路线0-＞11-＞12-＞0，总里程 17.9，节约里程 11.3；车 5：合并路线0-＞2-＞1-＞0，总里程8.53，节约里程7.37；车6：合并路线0-＞3-＞10-＞0，总里程 22.5，节约里程 1.1；总里程 136.97，比优化前的215.2节约36.35%。

当每车需承担3个超市的时候，程序的计算过程为：车1：合并路线 0-＞6-＞4-＞0，总里程 33.8，节约里程 25.6；合并路线0-＞6-＞4-＞5-＞0，总里程 37.3，节约里程 24.1；车 2：合并路线0-＞8-＞9-＞0，总里程 26.8，节约里程 16.4；合并路线0-＞8-＞9-＞7-＞0，总里程 27.47，节约里程 15.63；车 3：合并路线0-＞11-＞12-＞0，总里程17.9，节约里程11.3；合并路线0-＞10-＞11-＞12-＞0，总里程 21.9，节约里程 7.9；车 4：合并路线 0-＞2-＞1-＞0，总里程 8.53，节约里程 7.37；合并路线 0-＞2-＞1-＞3-＞0，总里程 14.43，节约里程5.8；总里程101.10，比优化前的215.2节约53.02%。

当每车需承担4个超市的时候，程序的计算过程为：车 1：合并路线 0-＞6-＞4-＞0，总里程33.8，节约里程 25.6；合并路线0-＞6-＞4-＞5-＞0，总里程37.3，节约里程24.1；合并路线0-＞6-＞4-＞5-＞8-＞0，总里程 49.2，节约里程 14.0；车 2：合并路线 0-＞7-＞9-＞0，总里程 17.24，节约里程 16.36；合并路线 0-＞1-＞7-＞9-＞0，总里程17.24，节约里程 8.4；合并路线 0-＞1-＞7-＞9-＞2-＞0，总里程 17.34，节约里程 7.4；车 3：合并路线 0-＞11-＞12-＞0，总里程 17.9，节约里程11.3；合并路线0-＞10-＞11-＞12-＞0，总里程21.9，节约里程7.9；合并路线 0-＞3-＞10-＞11-＞12-＞0，总里程32.5，节约里程1.1；总里程99.04，比优化前的215.2节约53.98%

可以看出优化后对于里程的节约还是十分显著的，而当我们知道不同容量的车行驶单位里程的价格以及根据实际情况，可以通过节约里程法找到最优的结果。

七、结束语

节约里程法并不是计算的最优的路线，而是一个较优的路线，计算最优的路线是一个NP完全问题（Non-deterministic Polynomial complete problem），无法在多项式的时间内找到结果（NP完全问题未必没有多项式算法，只是目前均没有找到），即使摒弃搜索算法而改使用高效的动态规划算法，时间复杂度依旧是指数级别的，这对于现实问题中配送中心需要配送门店的数目大量时候求解时间漫长到几年、几十年甚至更长，而节约里程法可以在极快的时间内求出一个比较优秀的结果，比起耗费大量人力物力而不切实际的求解最优解，使用节约里程法就显得更为经济有效了。

[1]陈晓伟、张悟移、耿继武：节约法在配送路线选择中的应用[J].昆明理工大学学报，2003（4）.

[2]李如姣：“节约里程法”在某物流公司配送中心的实际运用[J].科技资讯，2008（28）.