基于时间序列模型的可转换债券收益率的实证研究

曾立波黄丽芳

(湖南科技学院 数学与计算科学系，湖南 永州 425100)

1.引言

近年来,我国证券市场取得了突飞猛进的发展。随着证券市场的规模不断扩展,证券是市场内容不断加深,引入新的金融品种,完善市场结构已成为一种必然的趋势，上市公司和国有重点企业发行可转换债券就是一种新的尝试。可转换公司债券，是一种公司债券，它赋予持有人在发债后一定时间内，可依据本身的自由意志，选择是否依约定的条件将持有的债券转换为发行公司的股票或者另外一家公司股票的权利。对于投资者来说, 其吸引力主要在于相对安全的债务所带来的直接安全性,以及如果公司股票价格上涨债券可以转换成股权的可能性[1]。

由于可转换债券的价格与其收益率密切相关，因此对可转换债券收益率研究对其价格预测有极其重要的作用[2,3]。而时间序列模型在金融资产收益率研究方面应用相当广泛，因此本文利用时间序列模型和到2009年5月29日沪市上还在进行交易的全部7只可转换债券的数据进行实证分析。

2.转换债券收益率的实证分析

本文所选取的可转换债券是到2009年5月29日上海证券交易所所有还未到期和未赎回的7只可转换债券的数据，数据的选取时间为2008年10月23日-2009年5月31日。收益率采用J .P. Morgan银行的Risk Metrics方法中运用的对数收益率:

其中， Clpt和Clpt−1分别表示第t天和第t−1天的可转债的收盘价， Yt表示第t天的可转债的收益率。

本文所采用的时间序列模型为ARMA模型和AR− G ARCH 模型[4,5]。ARMA模型也称为自回归滑动平均模型。 A RMA(p ,q)模型为:

2．1 平稳性检验

由于上述时间序列模型都是针对平稳的时间序列而言的，因此我们首先必须对所选择的数据进行平稳性检验。本文采用单位根检验中的PP检验来判别收益率序列的平稳性。

首先用SAS软件对沪市可转换债券收益率序列}{tY进行平稳性检验，其PP检验的结果如下：

表1.市可转换债券收益率序列}{tY的平稳性检验表

从表一可以看出，由PP统计量(RHO,Tau)计算出来的概率值都为0.0010(<0.01),因此可以认为对数收益率序列 { Yt} 是平稳的。

2.2.型的选择和参数估计

ARMA模型的关键性假设之一就是误差的方差保持不变，而 A R− G ARCH 模型的误差的方差不为常量。因此数据的异方差性直接决定着模型的选取。所以下面必须对可转换债券收益率序列 { Yt} 进行异方差性检验。

表2.市可转换债券收益率序列}{tY的异方差性检验表

其中表二的LM统计量渐近服从 χ2(1)分布，并且只显示了滞后一阶的LM统计量的值及其对应的概率值。

通过对表二的数据的中的LM统计量对应的概率值与显著性水平0.05的比较，可以得到如下结论：

(1)可转换债券大荒和新钢的收益率有异方差性，因此可以用异方差模型进行拟合；

(2) 其他可转换债券的收益率无异方差性，因此可以用 A RMA(p ,q)模型进行拟合。

下面用SAS软件对选取的可转换债券的收益率进行 A RMA(p ,q)模型和异方差模型定阶和参数估计,其结果如下：

表3.RMA(p ,q)模型参数估计

表4.方差 A R (1) − G ARCH(1,1)模型参数估计

其中， A RMA(p,q)模型参数估计所使用的方法为极大似然估计和无条件最小二乘估计；异方差模型参数估计所使用的方法为极大似然估计；表三和表四的参数估计值都是显著的。

再分别对 A RMA(p,q)模型和异方差模型的残差进行Q统计量检验，其结果如下：

表5.RMA(p,q)模型的残差检验

我们通过对表五的第三列数据的观察，发现Q统计量对应的概率值均大于显著性水平0.05，所以可以认为：

（1）可转换债券澄星、赤化、恒源、南山、山鹰的对数收益率通过)2,2(ARMA模型过滤后的残差为白噪声。

（2）其他的可转换债券的对数收益率通过)1,2(ARMA模型过滤后的残差为白噪声。

表6.方差 A R (1) − G ARCH(1,1)模型的残差检验

从表六的 Q统计量对应的概率值均大于显著性水平 0.05，所以可以认为表中的所有可转换债券的对数收益率通过AR (1) − G ARCH(1,1)模型过滤后的残差为白噪声。

由此我们可以初步认为上述模型是合理的。

2.3.值模拟和分析

利用上面所得到的模型，通过蒙特卡洛模拟得到未来7天的收益率与实际收益率对比图如下：

图1.星、赤化、恒源转债模拟收益率与实际收益率对比图

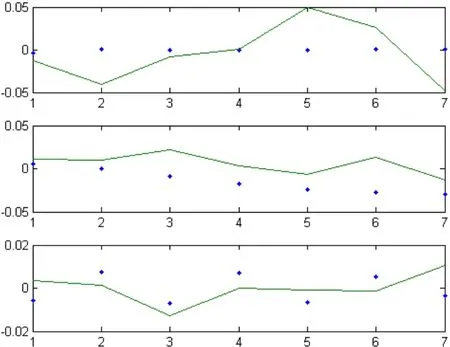
图2.鹰、南山、山鹰转债模拟收益率与实际收益率对比图

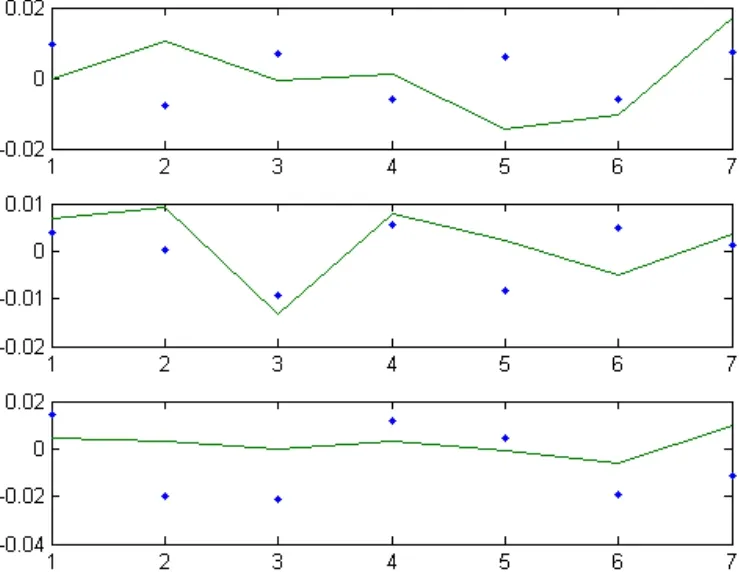
图3.洲、大荒、新钢转债模拟收益率与实际收益率对比图

从数值模拟的图像可以看出

（1）所有的模拟收益率都在实际收益率的上下波动，说明时间序列模型可以对可转换债券的收益率进行短期的预测。

（2）模拟得到的收益率与实际收益率存在一定的误差，说明得到的模型还是不能反映出实际收益率的全部变化情况。产生这种情况的原因可能有如下两种可能：一种是由于得到模型不够准确，另一种就是时间序列模型本身就无法准确的描述可转换债券的收益率。

(3) 使用 ARMA模型模拟的可转换债券的收益率体现出的实际收益率的波动性不是很明显，但是使用异方差模型模拟的两只可转换债券的收益率更能体现出实际收益率的波动性。

3.束语

由于时间序列模型在模拟金融资产收益率方面有着广泛的应用，因此本文利用到2009年5月25日沪市还在进行交易的可转换债券的收盘价对时间序列模型在其收益率模拟方面的应用进行了实证，结果发现对于可转换债券的收益率的模拟结果是不能让人满意的，这有可能是由于如下三个原因所致：（1）时间序列模型不能很好的刻画可转换债券包含有期权的价值；（2）外界因素（如全球金融危机，国家出台的重大政策，自然灾难等）对金融资产特别是对可转换债券收益率的影响在时间序列模型中没有很好的体现出来；（3）我国证券市场上的可转换债券发展还不够完善。

[1]刘立喜.可转换公司债券[M].上海:上海财经大学出版社，1999.

[2]BrennanM,Schwartz E. Analyzing convertible bonds[J]. Journal of Financial and Quantitative Analysis,15(4): 907- 929., 1980.

[3]Manuel Ammann a, Axel Kind, Christian Wilde. Are convertible bonds underpriced?An analysis of the French market[J].Journal of Banking & Finance 27:635–653, 2003.

[4]James D. Hamilton.Time series analysis[M].Prinston University Press.1994.

[5]Ruey S. Tsay.金融时间序列分析[M].北京:机械工业出版社.2006.4.