灾后应急救援运输路径优化模型研究

任其亮，乔 丹

(重庆交通大学交通运输学院，重庆400074)

REN Qi-liang，QIAO Dan

(School of Traffic＆ Transportation，Chongqing Jiaotong University，Chongqing 400074，China)

特大自然灾害以其突发性和毁灭性而受到高度重视，因灾后救援物资的运输情况十分复杂，在很多方面具有不确定性，使救援物资的运输调度在灾后应急救援中占有非常重要的位置。目前的应急救援运输研究大都是基于确定的路径，主要依靠经验，从时间、费用、危险性等方面做定性或半定量分析［1－3］。笔者从灾后救援运输的实际出发，其各种不确定性，建立运输路径的不确定优化模型，并探讨模型的求解算法。

1 灾后救援运输的不确定性因素

灾后救援物资运输的特殊性在于时间的紧迫性和多因素不确定性［4］。救援运输网络优化模型的不确定性包括变量的不确定性、约束条件的不确定性、决策目标的不确定性等，具体表现为:

1)网络可靠度不确定性。网络可靠度是指网络在规定的时间和条件下完成预定功能的概率，是衡量交通网络在紧急灾害情况下，系统功效能否正常发挥、运行状态是否达到预期要求的重要指标［2］。由于对灾区的具体环境不了解，救援运输网络的节点及其各路段受灾情况的不同，对整个救援的网络不清楚。运输网络的节点和路段可能在某一时刻遭到毁坏，毁坏后又可能在某一时刻得到修复;另一方面发生灾害后，救援车辆异常增加，加之人员的盲目流动，会造成某些路段交通量骤增，运输网络可靠度是不确定的。

2)容量可靠度不确定性。路网容量可靠性［5］是指在一定的服务水平下，路网容量能满足一定交通需求水平的概率。受灾后，由于各类路段毁坏的程度是不确定的，因此，救援物资运输网络的容量可靠性是不确定的。

3)运输时间不确定性。由于运输网络各路段遭受灾害的破坏程度是不确定的，而运输梯队通过遭受不同程度的破坏路段的时间是不确定的，救援运输梯队通过不同路径的时间常常是不确定的。

4)运输物资需求量不确定性。在救援物资运输的时间段，次生灾害随时可能发生，造成更多的人员伤亡和财产损失，并且往往会破坏通信和电力设施，给指挥协调和信息反馈造成不利，无法确切得到救援物资需求量。因此，运输物质的需求量也具有不确定性。

5)运输损耗不确定性。灾害对交通设施的破坏，使得运输梯队通过路段时会产生损耗。由于各路段遭受的破坏程度是不确定的，其造成的运输损耗也是不确定的。因此，运输梯队通过网络路段时的运输损耗也是不确定的。

6)多重目标下选择不确定性。灾后救援运输路径选择中，当多个目标发生冲突时该如何选择，如当选择一条运输路径时，运输时间最少，而运输损耗又比较多，而这时要达到运输时间和运输损耗的最优化，该如何选择?由于救援任务的需要，2个指标往往都是路径决策的重要因素，不能只考虑某一方面，且在很多时候这些因素是不确定的，即路径优化问题是一个在不确定性环境下的多目标优化问题。

2 救援运输路径优化模型

2.1 网络图

根据灾后救援运输任务的特点，将交通网络抽象为一个有向赋权图G=(V，E，C)。式中:V={1，2，…，n}是节点的集合(n为节点个数)，若i，j∈V，则xij表示从i到j的一条弧;E为弧集，可以表示成以下网络结构:x={xij:1≤i≤n－1，i+1≤j≤n}，其中，xij∈{0，1}，xij=1 表示路段xij在选择的可行路径上，否则xij=0;C为弧xij的权集，可以是弧的运输时间、运输损耗和可靠度的集合。

假设节点完全可靠，而节点之间的连接失效与否是彼此统计独立的，且失效的概率已知，那么在V的子集K中的所有节点是否连接成功是一个随机事件，把这个时间的概率称为K，即节点可靠性，记做R(K，x)，其中x为网络结构。如果K中的所有节点在G中都是连通的，那么称这个网络G是K连通的。因此，K节点可靠性R(K，x)=Pr{G相对网络结构x是K连通}，当K=G时，K节点可靠性R(K，x)就是网络可靠性［6］。

2.2 约束条件

2.2.1 目标约束

灾后救援运输的路线选择中，一般行驶时间这个参数最为重要，行驶时间越短的道路越适合作为灾害后的紧急救援道路［2］。灾后应急救援运输的目标是在运输时间、运输路径可靠度和运输损耗以一定的置信水平不超过目标值，从而使救援运输效率达到最高，使灾区能在第一时间内得到物资供应［7］。因此，假设有如下目标优先级结构:第1优先级:时间目标，在给定的置信水平α1下，运输时间应尽可能的不超过目标值b1;第2优先级:可靠性目标，网络可靠性尽可能以置信水平α2不低于目标值b2;第3优先级:损耗目标，运输损耗尽可能以置信水平α3不超过目标值b3。

2.2.2 路径约束

灾后救援运输路径优化问题的约束，假设:1)运输路径起终点均只有一个且是确定的;2)单梯队从起点出发，只能选择一条路段作为运输道路，最后到达终点;

3)网络中任意中间节点vi，梯队进入该节点，必须还要从该节点出发，不得停留或消失;

4)梯队通过各路段的时间和损耗是随机的;

5)运输网络可靠性是随机的。

可得路径约束方程如下:

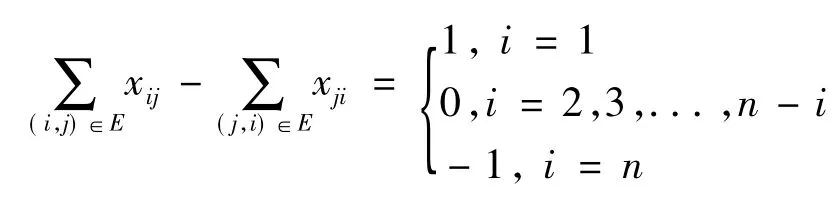
2.3 目标规划模型

令tij表示弧vij的通行时间，且记t={tij│(i，j) ∈V}，那么路径x的通行时间就可以写成f(x，t)=令sij表示弧vij的通行损耗，且记是s={sij│(i，j)∈V}，那么路径x的通行损耗就可以写成

根据不确定机会约束理论［6］，得机会约束目标规划模型约束为:

式中:lexmin{*}为按字典序极小化目标向量;Pr{*}为事件的概率;αi(i=1，2，3)为给定的置信;bi(i=1，2，3)为给定的目标值;为目标i偏离目标值bi(i=1，2，3)的乐观正偏差;x为路径决策变量，且x={xij:1≤i≤n－1，i+1≤j≤n}(n为网络节点的个数，xij∈{0，1}，xij=1表示路段xij在选择的可行路径上，否则xij=0)。

3 模型求解

3.1 算法

为求解不确定规划模型，笔者设计了基于遗传算法的混合智能算法:首先利用随机模拟［6］产生不确定函数的训练样本;然后利用这些数据训练神经元网络［8］以逼近不确定函数;最后把训练好的神经元网络嵌入到遗传算法中。根据灾后救援运输的特殊情况，对遗传算法中的因素做以下说明:

1)编码。采用十进制编码构造染色体，染色体的基因对应网络节点序号，而序号的排列顺序代表救援运输梯队从起点到终点的路径。设路网的节点集合V中节点总数为n，则染色体的基因总数也为n。染色体基因的组成方式:第1个为起点序号“1”;接下来是中间节点，设中间节点总数为n，则有0≤l≤n－2;然后是终点“n”。如果 0≤l＜n－2，则在“n”点后补“0”，使基因总数保持为n。设染色体中从“1”到“n”的非0基因个数为m，定义其为有效基因数。以图1为例，建立路径1－2－3－6－7的连接矩阵(表1)，则该路径对应的染色体的编码为1 2 3 6 7 0 0。

图1 网络图Fig.1 Network diagram

表1 连接矩阵Tab.1 Connection matrix

基于这样的编码方式，可得出染色体中的第1个基因是“1”，最后一个不为“0”的基因是终点的序号“n”，当基因中包含“0”基因时，说明有部分节点没有在这个染色体所代表的路径上。

2)评价函数。比较常用的评价函数是基于序的评价函数［6］，设目前该代中的染色体为T1，T2，…，Tpop_size，对于目标规划模型，种群中的染色体有以下序关系:对于2个染色体，如果它们在高一级的目标值相同，则在当前一级中染色体所对应的目标值越小越好。如在每一级中2个染色体都对应相同的目标值，就认为这2个染色体无差别，从而可以对它们进行随机的排序。设参数α∈(0，1)给定，定义基于序的评价函数为:eval(Ti)=a(1－a)i－1，i=1，2，…，pop_size 。

3)选择。采用改进的轮盘赌选择法。在选择新个体时，首先在当前代中选择最佳个体直接进入下一代(若有多个，则随机选取一个)，然后对其它个体依累积概率大小采用轮盘赌方式进行选择。对每个染色体Ti，计算累计概率1，2，…，pop_size 。从区间(0，qpop_size)中产生一个随机数r，若qi－1＜r≤qi，则选择第i个染色体Ti，重复选择，得到pop_size个复制的染色体。

4)交叉。根据染色体编码规则的特点及与路径节点序号的关联性，采用类OX法作为染色体交叉的方法，交叉步骤为:①从上一代选择染色体T0、T1的基因中随机选择2个交叉点，交叉点必须同时位于2个染色体的“1”之后，“n”之前，以保证“0”基因不被交叉，交叉点之间的部分为匹配区域段;②将T0的匹配段加到T1的基因“1”之后，将T1的匹配区域加到T0的基因“1”之后;③消除染色体匹配段后面的重复节点。

5)变异。采用的染色体变异方式有3种:①在基因“1”和“n”之间随机删除一个非必经点所代表的基因，同时在“n”后补“0”基因，以使保持基因数为n;②当有效基因总数m＜n时，增加一个基因中没有的节点序号作为基因，其位置可以在有效基因的中间部份随机选取，同时在“n”后删除一个“0”基因;③互换“1”和“n”之间的2个基因。为提高遗传算法的性能，笔者采用类似于模拟退火算法中的Metropolis准则［1］对变异进行改进，如果变异后的值优于变异前的值，则新染色体进入下一代;否则，依概率确定是否进入下一代。公式如下代中的适应度最大值，P为变异后染色体接受概率。

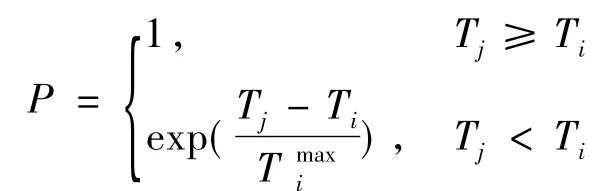
3.2 算例

以图1为救援运输网络图，对建立的目标规划模型进行试验，以验证模型和算法的有效性。

单梯队通过各路段的随机时间和通行损耗分布如表2和表3。路网各路段的可靠性服从正态分布N(1，4)。

表2 通行时间随机分布Tab.2 Random distribution of time

表3 通行损耗随机分布Tab.3 Random distribution of loss

根据网络节点数，染色体的基因个数为7。在置信水平(α1，α2，α3)=(0.8，0.85，0.8)下，通行时间、路网可靠性和通行损耗的目标水平为(b1，b2，b3)=(5，0.85，5)。设遗传算法的种群大小为 50，交叉概率 0.85，变异率 0.05。

通过运行混合智能算法(1 000次模拟循环，500次遗传迭代)，得到最优路径为1－3－7，它满足前2个目标，第3个目标偏差为0.975。

4 结语

从灾后救援运输的角度出发，建立灾后救援运输路径动态优化模型和算法。该模型能符合发生各类特大自然灾害时的实际情况，解决不确定性救援运输路径动态优化问题，满足各类特大自然灾害时的救援运输需求，并指导其他紧急状态下的运输问题，能够为极大地减少因现有理论方法不足而产生的人员、物资的损耗问题提供借鉴，提高救援运输的效率，具有较高的社会经济效益。

［1］黄金虎.应急物流系统若干关键技术的研究与实现［D］.上海:上海交通大学，2007.

［2］巴桑次仁，邓桂英，巴桑央金.西藏地震应急救援体系建设的探索［J］.高原地震，2009，21(2):58 －61.

［3］王洪，陆愈实，王莎莎.基于MATLAB的应急救援最优路径选择［J］.工业安全与环保，2009，35(5):48－50.

［4］繆成，许维胜，吴启迪.大规模应急救援物资运输模型的构建与求解［J］.系统工程，2006，24(11):6 －12.

［5］任其亮.灰色马尔可夫模型在公路运量弹性系数预测中的应用研究［J］.重庆交通大学学报:自然科学版，2009，28(2):290－293.

［6］石玉峰.战时不确定性运输路径优化研究［D］.成都:西南交通大学，2006.

［7］彭锦，刘宝碇.不确定规划的研究现状及其发展前景［J］.运筹与管理，2002，11(2):1 －10.

［8］陈燕燕，刘小明，梁颖.可靠度在交通系统规划与管理中的应用［M］.北京:人民交通出版社，2006.